
- •1. Вычислительный эксперимент. Типы погрешностей. Погрешность округления. Представление чисел на эвм.
- •2. Накопление погрешностей округления.
- •3. Метод Гаусса. Подсчет числа действий. Метод Гаусса с выбором главного элемента.
- •4. Условия применимости метода Гаусса и метода Гаусса с выбором главного элемента.
- •5.Обусловленность, устойчивость решения слу
- •6.Итерационные методы решения линейных уравнений. Метод Якоби, Зейделя.
- •7.Достаточное условие сходимости стационарных итерационных методов.
- •8. Сходимость метода Якоби, Зейделя, метода простых итераций.
- •9. Необходимое и достаточное условие сходимости.
- •10. Оценка скорости сходимости итерационных методов в случае симметричных матриц a и b
- •11. Многочлен Чебышева с нормировкой по старшему коэффициенту.
- •12. Многочлен Чебышева с нормировкой по значению многочлена в нуле
- •13. Явный итерационный метод Чебышева
- •14. Неявный итерационный метод Чебышева.
- •15. Метод минимальных поправок, метод минимальных невязок
- •16. Метод скорейшего спуска, метод сопряжённых градиентов. Подсчёт числа итераций для решения системы линейных уравнений с точностью до ℰ итерационными методами.
- •17. Интерполирование и приближение функций. Интерполяционная формула Лагранжа.
- •18. Погрешность интерполяции. Оптимальный выбор узлов интерполяции.
- •19. Сходимость интерполяционных процессов. Интерполяция с кратными узлами.
- •20. Интерполяция кубическими сплайнами.
- •21. Скорость процесса интерполяции кубическими сплайнами.
- •22. Наилучшее приближение в гильбертовом пространстве.
- •23. Численное интегрирование. Формула прямоугольника, трапеции, Симпсона. Оценка погрешности.
- •24. Апостерионная оценка погрешности методом Рунге. Автоматический выбор шага интегрирования.
- •25. Численное дифференцирование. Связь между точностью вычисления функции и шагом сетки.
- •26. Решение нелинейных уравнений методом простых итераций, релаксации. Сходимость метода релаксации.
- •27. Сходимость метода простых итераций
- •28. Метод Ньютона. Сходимость метода Ньютона.
- •29. Метод Ньютона в случае кратных корней. Односторонние приближения по методу Ньютона.
- •30. Итерационные методы решения снлу. Сходимость метода простых итераций
- •31. Производная от оператора. Метод Ньютона для систем нелинейных уравнений.
- •32. Метод Рунге-Кутта второго порядка. Семейство методов второго порядка. Методы третьего и четвертого порядка.
- •1. Методы второго порядка
- •2. Методы третьего порядка.
- •3. Методы четвертого порядка.
- •33. Доказательство сходимости метода Рунге-Кутта.
- •34. Многошаговые разностные методы. Погрешность аппроксимации метода.
- •35. Устойчивость многошагового метода по начальным данным.
- •36. Оценка решения неоднородного разностного уравнения. Устойчивость многошагового метода по правой части.
- •37. Разностная аппроксимация Пуассона. Порядок аппроксимации
- •38. Оператор 2 разностной производной на отрезке. Собственные функции и собственные значения оператора
- •39.Разностный оператор Лапласа. Собственные значения и собственные функции
- •40. Устойчивость и сходимость разностной аппроксимации уравнения Пуассона.
- •1) Метод простых итераций.
- •2) Метод Чебышева.
- •3) Метод сопряжённых градиентов.
- •45. Асимптотическая устойчивость разностных схем.
- •46. Вариационные методы в математической физике.
- •47. Метод Ритца.
- •48. Метод Галеркина.
48. Метод Галеркина.
Опишем этот
метод применительно к решению операторного
уравнения
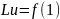 в
гильбертовом пространстве F(Ф(L)
плотно в F), где
в
гильбертовом пространстве F(Ф(L)
плотно в F), где
 симметричный
и положительно определенный оператор
и Ф(
симметричный
и положительно определенный оператор
и Ф(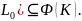
Введем
последовательность конечномерных
подпространств
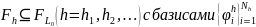 .
Тогда приближение по Галеркину ищется
в виде
.
Тогда приближение по Галеркину ищется
в виде
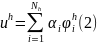 ,
где
,
где
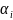 выбираются так чтобы невязка
выбираются так чтобы невязка
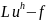 была
ортогональна всем элементам из
,
т.е.
была
ортогональна всем элементам из
,
т.е.
( s=1,…,
s=1,…,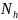
Получаем
систему
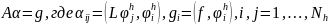
После нахождения
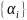 приближенное
решение легко находим по (2).
приближенное
решение легко находим по (2).
Сходимость
приближенных решений (2). Если u
–решение задачи (1) существует и
единственно в F и оператор
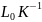 вполне
непрерывен в F, то
последовательные приближения
вполне
непрерывен в F, то
последовательные приближения
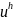 ,
получаемые методом Галеркина, сходятся
в F к точному решению u.
,
получаемые методом Галеркина, сходятся
в F к точному решению u.
Рассмотрим
одну из модификаций метода Галеркина,
где
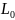 не
является симметричным и положительно
определенным. Пусть существует
ограниченный оператор
не
является симметричным и положительно
определенным. Пусть существует
ограниченный оператор
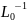 .
Тогда (1) эквивалентно
.
Тогда (1) эквивалентно
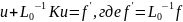 (2)
(2)
 (
(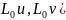 и
нормой
и
нормой
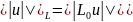
Метод Галеркина
для уравнения (2). Пусть
-конечномерные
подпространства из
с базисами
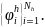 Приближенное решение ищется в виде
Приближенное решение ищется в виде
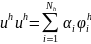 ,
где неизвестные
,
где неизвестные
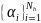 определяется
из системы линейных уравнений
определяется
из системы линейных уравнений
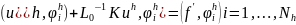
Алгоритм построения базисных функций:
Пусть область
значений оператора K и
функции f принадлежат
F(K,f)⊆F.
Зададим в F(K,f)
систему координатных функций
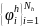 ,
полную в F(K,f).
,
полную в F(K,f).
Построим

