
- •1. Вычислительный эксперимент. Типы погрешностей. Погрешность округления. Представление чисел на эвм.
- •2. Накопление погрешностей округления.
- •3. Метод Гаусса. Подсчет числа действий. Метод Гаусса с выбором главного элемента.
- •4. Условия применимости метода Гаусса и метода Гаусса с выбором главного элемента.
- •5.Обусловленность, устойчивость решения слу
- •6.Итерационные методы решения линейных уравнений. Метод Якоби, Зейделя.
- •7.Достаточное условие сходимости стационарных итерационных методов.
- •8. Сходимость метода Якоби, Зейделя, метода простых итераций.
- •9. Необходимое и достаточное условие сходимости.
- •10. Оценка скорости сходимости итерационных методов в случае симметричных матриц a и b
- •11. Многочлен Чебышева с нормировкой по старшему коэффициенту.
- •12. Многочлен Чебышева с нормировкой по значению многочлена в нуле
- •13. Явный итерационный метод Чебышева
- •14. Неявный итерационный метод Чебышева.
- •15. Метод минимальных поправок, метод минимальных невязок
- •16. Метод скорейшего спуска, метод сопряжённых градиентов. Подсчёт числа итераций для решения системы линейных уравнений с точностью до ℰ итерационными методами.
- •17. Интерполирование и приближение функций. Интерполяционная формула Лагранжа.
- •18. Погрешность интерполяции. Оптимальный выбор узлов интерполяции.
- •19. Сходимость интерполяционных процессов. Интерполяция с кратными узлами.
- •20. Интерполяция кубическими сплайнами.
- •21. Скорость процесса интерполяции кубическими сплайнами.
- •22. Наилучшее приближение в гильбертовом пространстве.
- •23. Численное интегрирование. Формула прямоугольника, трапеции, Симпсона. Оценка погрешности.
- •24. Апостерионная оценка погрешности методом Рунге. Автоматический выбор шага интегрирования.
- •25. Численное дифференцирование. Связь между точностью вычисления функции и шагом сетки.
- •26. Решение нелинейных уравнений методом простых итераций, релаксации. Сходимость метода релаксации.
- •27. Сходимость метода простых итераций
- •28. Метод Ньютона. Сходимость метода Ньютона.
- •29. Метод Ньютона в случае кратных корней. Односторонние приближения по методу Ньютона.
- •30. Итерационные методы решения снлу. Сходимость метода простых итераций
- •31. Производная от оператора. Метод Ньютона для систем нелинейных уравнений.
- •32. Метод Рунге-Кутта второго порядка. Семейство методов второго порядка. Методы третьего и четвертого порядка.
- •1. Методы второго порядка
- •2. Методы третьего порядка.
- •3. Методы четвертого порядка.
- •33. Доказательство сходимости метода Рунге-Кутта.
- •34. Многошаговые разностные методы. Погрешность аппроксимации метода.
- •35. Устойчивость многошагового метода по начальным данным.
- •36. Оценка решения неоднородного разностного уравнения. Устойчивость многошагового метода по правой части.
- •37. Разностная аппроксимация Пуассона. Порядок аппроксимации
- •38. Оператор 2 разностной производной на отрезке. Собственные функции и собственные значения оператора
- •39.Разностный оператор Лапласа. Собственные значения и собственные функции
- •40. Устойчивость и сходимость разностной аппроксимации уравнения Пуассона.
- •1) Метод простых итераций.
- •2) Метод Чебышева.
- •3) Метод сопряжённых градиентов.
- •45. Асимптотическая устойчивость разностных схем.
- •46. Вариационные методы в математической физике.
- •47. Метод Ритца.
- •48. Метод Галеркина.
46. Вариационные методы в математической физике.
Рассмотрим
функционал

 -заданная
функция, непрерывная вместе с производными
до второго порядка.
-заданная
функция, непрерывная вместе с производными
до второго порядка.

Возьмем функцию
 .
.
Найдем условие
того, чтобы функционал
 в -окрестности имел экстремум.
в -окрестности имел экстремум.
Рассмотрим

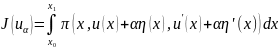
Разложим в ряд
Тейлора по параметру
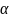 :
:

 –
вариация 1-го порядка функционала
–
вариация 1-го порядка функционала

Проинтегрируем
по частям

Чтобы
 имел экстремум
имел экстремум
 должна удовлетворять:
должна удовлетворять:
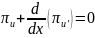 - уравнение Эйлера
- уравнение Эйлера
В качестве
примера рассмотрим задачу Для задачи
 (1)
(1)
Где и достаточно гладкие функции.
Рассмотрим
вариационный функционал

Уравнение
Эйлерадля этого функционала:

Тогда из соотношения (3)
⇨
Это значит, что если каждая функция из области определения функционала будет удовлетворять условию (5), то экстремум функционала (2) на таких функциях будет доставлять решение задачи (1).
Пусть

Пространство функций, удовлетворяющих (6), образует Ф(A)⇨ (4) перепишем
Au=f,
 Ф(A)
Ф(A)
Рассмотрим

Пусть
. Тогда уравнением Эйлера будет Au=f,
Ф(A) (8),соответствующая
вариационной задаче (9)
(9)
Найдем условия, при которых задачи (8) и (9) эквивалентны.
Рассмотрим Au=f, где А- линейный, положительный, самосопряженный оператор с областью определения Ф(A).
Если существует решение (8), то оно доставляет минимум функционалу
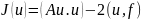
Докажем это, пустьu0 – решение (1) ⇨Au0=f.
Пусть η
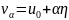

Т.к. А-самосопр
опреатор, то

Т.к. А>0 ⇨ .
Это значит, что минимум функционала
.
Это значит, что минимум функционала
 достигается на решении
достигается на решении
 .
Имеет место и обратное утверждение:
элемент
.
Имеет место и обратное утверждение:
элемент
 гильбертова пространства, доставляющий
минимум функционалу Jи
принадлежащий
гильбертова пространства, доставляющий
минимум функционалу Jи
принадлежащий
 ,
является решением Au=f
,
является решением Au=f
47. Метод Ритца.
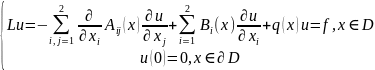 (1)
(1)
Пусть
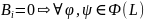 выполняется:
выполняется:
 (2)
(2)
Поставим теперь
в соответствие исходной задаче
вариационную задачу на нахождение
элемента
 ,
на котором достигается минимум функционала
,
на котором достигается минимум функционала
 (3)
(3)
Из (2) видно,
что область определения
 .
.
Введем скалярное произведение:
 =
= =
= и
соответствующую норму
и
соответствующую норму

 полное
нормированное пространство, порожденное
оператором L.
полное
нормированное пространство, порожденное
оператором L.
Если

Наиболее
известным методом решения задачи (4)
является метод Ритца. Опишем его
применительно к решению операторного
уравнения Lu=f(5),
гдеL – самосопряженный,
положительно определенный оператор.
(5) равносильно нахождению элемента
гильбертова пространства
 ,
реализующего минимум функционала
,
реализующего минимум функционала

Введем
последовательность конечномерных
подпространств
 ,
которые определяются бесконечной
последовательностью
,
которые определяются бесконечной
последовательностью
 .
.
{ }-
полна в
,
если
}-
полна в
,
если

(т.е.
 может
быть с любой степенью точности
аппроксимирован элементами пространств
)
может
быть с любой степенью точности
аппроксимирован элементами пространств
)
В предложенной постановке метод Ритца формулируется следующим образом:
Требуется
найти элемент
 минимизирующий
в пространстве
.
минимизирующий
в пространстве
.
Если L
положительно определен в
и { полна
в
полна
в
 последовательность приближений {
последовательность приближений {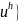 по
Ритцу сходится в
к решению uуравнения (5).
по
Ритцу сходится в
к решению uуравнения (5).
Если базис
пространства
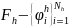 ,
то задача нахождения
равносильна нахождению коэффициентов
,
то задача нахождения
равносильна нахождению коэффициентов
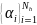 разложения
разложения
 из
условия минимума функционала J.
Подставляя разложение в функционал J
и приравнивая к 0
из
условия минимума функционала J.
Подставляя разложение в функционал J
и приравнивая к 0
 ,
приходим к системе линейных алгебраических
уравнений
,
приходим к системе линейных алгебраических
уравнений
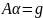 ,
где
,
где

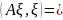 при
при
 положительно определна.
положительно определна.
