
- •1. Вычислительный эксперимент. Типы погрешностей. Погрешность округления. Представление чисел на эвм.
- •2. Накопление погрешностей округления.
- •3. Метод Гаусса. Подсчет числа действий. Метод Гаусса с выбором главного элемента.
- •4. Условия применимости метода Гаусса и метода Гаусса с выбором главного элемента.
- •5.Обусловленность, устойчивость решения слу
- •6.Итерационные методы решения линейных уравнений. Метод Якоби, Зейделя.
- •7.Достаточное условие сходимости стационарных итерационных методов.
- •8. Сходимость метода Якоби, Зейделя, метода простых итераций.
- •9. Необходимое и достаточное условие сходимости.
- •10. Оценка скорости сходимости итерационных методов в случае симметричных матриц a и b
- •11. Многочлен Чебышева с нормировкой по старшему коэффициенту.
- •12. Многочлен Чебышева с нормировкой по значению многочлена в нуле
- •13. Явный итерационный метод Чебышева
- •14. Неявный итерационный метод Чебышева.
- •15. Метод минимальных поправок, метод минимальных невязок
- •16. Метод скорейшего спуска, метод сопряжённых градиентов. Подсчёт числа итераций для решения системы линейных уравнений с точностью до ℰ итерационными методами.
- •17. Интерполирование и приближение функций. Интерполяционная формула Лагранжа.
- •18. Погрешность интерполяции. Оптимальный выбор узлов интерполяции.
- •19. Сходимость интерполяционных процессов. Интерполяция с кратными узлами.
- •20. Интерполяция кубическими сплайнами.
- •21. Скорость процесса интерполяции кубическими сплайнами.
- •22. Наилучшее приближение в гильбертовом пространстве.
- •23. Численное интегрирование. Формула прямоугольника, трапеции, Симпсона. Оценка погрешности.
- •24. Апостерионная оценка погрешности методом Рунге. Автоматический выбор шага интегрирования.
- •25. Численное дифференцирование. Связь между точностью вычисления функции и шагом сетки.
- •26. Решение нелинейных уравнений методом простых итераций, релаксации. Сходимость метода релаксации.
- •27. Сходимость метода простых итераций
- •28. Метод Ньютона. Сходимость метода Ньютона.
- •29. Метод Ньютона в случае кратных корней. Односторонние приближения по методу Ньютона.
- •30. Итерационные методы решения снлу. Сходимость метода простых итераций
- •31. Производная от оператора. Метод Ньютона для систем нелинейных уравнений.
- •32. Метод Рунге-Кутта второго порядка. Семейство методов второго порядка. Методы третьего и четвертого порядка.
- •1. Методы второго порядка
- •2. Методы третьего порядка.
- •3. Методы четвертого порядка.
- •33. Доказательство сходимости метода Рунге-Кутта.
- •34. Многошаговые разностные методы. Погрешность аппроксимации метода.
- •35. Устойчивость многошагового метода по начальным данным.
- •36. Оценка решения неоднородного разностного уравнения. Устойчивость многошагового метода по правой части.
- •37. Разностная аппроксимация Пуассона. Порядок аппроксимации
- •38. Оператор 2 разностной производной на отрезке. Собственные функции и собственные значения оператора
- •39.Разностный оператор Лапласа. Собственные значения и собственные функции
- •40. Устойчивость и сходимость разностной аппроксимации уравнения Пуассона.
- •1) Метод простых итераций.
- •2) Метод Чебышева.
- •3) Метод сопряжённых градиентов.
- •45. Асимптотическая устойчивость разностных схем.
- •46. Вариационные методы в математической физике.
- •47. Метод Ритца.
- •48. Метод Галеркина.
38. Оператор 2 разностной производной на отрезке. Собственные функции и собственные значения оператора
Рассмотрим разностное уравнение:
 (1)
(1)
На
сетке

Соответствующая краевая задача:
 (2)
(2)

где
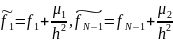


Рассмотрим
множество векторов

Определим оператор A:


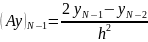
Система
(3):
 ,
где
,
где
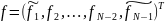
Оператор
A
задан на множестве H-пространство
функций, заданных на
 и
=0 на
и
=0 на

 (6)-оператор
2 разностной производной
(6)-оператор
2 разностной производной
Необходимо найти собственные значения и собственные функции оператора А

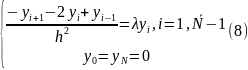
Или
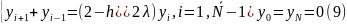
Разностная задача (8) является аппроксимацией задачи

 ищем
собственные функции задачи (8) в виде
ищем
собственные функции задачи (8) в виде

Поставим
(11) в (9) =>

Функция (11) является собственной функцией оператора (6), если
 =>
=>
При
 получим N-1 различных собственных
значений и собственных функций
получим N-1 различных собственных
значений и собственных функций
Свойства:


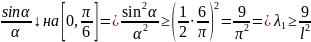
Введем

Покажем
что
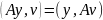

Оператор (6) самосопряженный => его собственные функции ортогональны

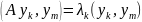
 =>
=>
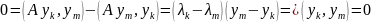



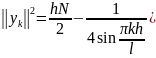
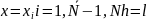

39.Разностный оператор Лапласа. Собственные значения и собственные функции
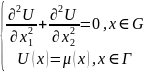 (1)
(1)
Разностный оператор Лапласа:

Сетка

Введем
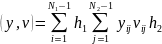

:
Покажем, что A- самосопряженный
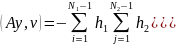
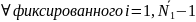



Где
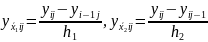 =>
=>


Т.к. y и v симметрично =>
Собственные числа и собственные функции


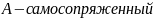
Обозначим
 ,
,




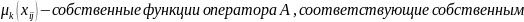

Имеем
( )
(
)
( )
собственных функций образующих в H
ортогональный базис
)
собственных функций образующих в H
ортогональный базис
Если
 -ортогональны
-ортогональны
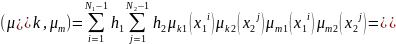

Свойства:





40. Устойчивость и сходимость разностной аппроксимации уравнения Пуассона.
Устойчивость по граничным условиям.
Рассмотрим задачу Дирихле для уравнения Пуассона

 (1)
(1)
в
прямоугольнике
 с границей
с границей
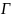 .
Была введена сетка
.
Была введена сетка
 ,
,
где
 ,
и построена разностная схема второго
порядка аппроксимации
,
и построена разностная схема второго
порядка аппроксимации

 (2)
(2)
Здесь
 множество внутренних узлов сетки
множество внутренних узлов сетки
 и
и
 — множество граничных узлов:
— множество граничных узлов:
 ,
,
 .
.
1) Метод простых итераций.
Общий вид одношагового итерационного метода:
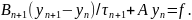
Пусть

Оптимальный выбор числа таков:
 ,
,
где
 ,
,
 .
.
Тогда
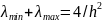 .
Следовательно,
.
Следовательно,
 .
.
Итерационный процесс примет вид:
 . (3)
. (3)
Тогда
 , (4)
, (4)
где
 невязка.
невязка.
2) Метод Чебышева.
Явный метод Чебышева. Итерации вычисляются по следующей формуле:
 , (5)
, (5)
где
 ,
,
где
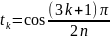 ;
; 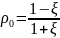 ;
; 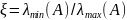 ;
; 
За
начальное приближение можно взять
произвольное

3) Метод сопряжённых градиентов.
Рассмотрим итерационный процесс:
 ,
,
где
 заданное
начальное приближение, а
заданное
начальное приближение, а
 вычисляется
по одношаговой формуле
вычисляется
по одношаговой формуле
 ,
,
 . (6)
. (6)
Пусть
.
Введём обозначения:
 невязка;
невязка;
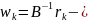 поправка.
поправка.
Тогда
при выборе
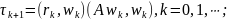

величина
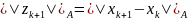 будет минимальной.
будет минимальной.
Оценки.
) Для метода простых итераций поставленных условиях справедлива оценка:
 ,
(7)
,
(7)
где
 .
.
Число итераций, для достижения точности равна

Так
как при
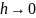 верно, что
верно, что
 ,
то
,
то
 Значит:
Значит:

2) Для методы Чебышева и метода сопряжённых градиентов верна та же оценка (7), но при

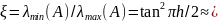 .
.
Число итераций, для достижения точности равна
 .
.
Тогда
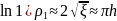 и
и

45. Асимптотическая устойчивость разностных схем.
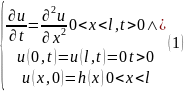 Решение:
Решение:

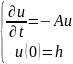
 В
данном случае СФ для
–
В
данном случае СФ для
–
 ,
,
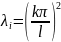
 При
При
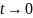 медленнее всех
медленнее всех
 член
с
член
с

 Потребуем,
чтобы для решения задачи (3) выполняется
оценка:
Потребуем,
чтобы для решения задачи (3) выполняется
оценка:
 где
где


 Свойство
(4) – асимптотическая устойчивость
Для
решения задачи (3) справедливо:
Свойство
(4) – асимптотическая устойчивость
Для
решения задачи (3) справедливо:
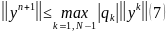
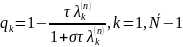 где
где
 – СЗ оператора второй разностной
производной:
– СЗ оператора второй разностной
производной:

Устойчивость
по начальным данным обеспечивается


Лемма 1
Если
 и
и
 и
и
 ,
,

Доказательство
Из
(5), (6)
 ,
,
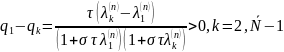
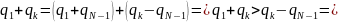


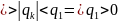 Из
(5), (6)
Из
(5), (6)

Следствие 1
Если
выполнены условия Леммы 1
для
решения (3) выполняется
 ,
где
,
где
 (следует из (7), (6)
(следует из (7), (6)
Следствие 2
Если
выполнены условия Леммы 1 и
 не зависит от
не зависит от
 схема
(3) асимптотически устойчива.
схема
(3) асимптотически устойчива.
Доказательство
Т.
к.
 необходимо,
то достаточно показать, что
необходимо,
то достаточно показать, что
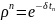 ,
где
,
где



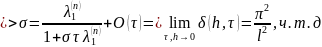 неравенство
неравенство
 является
условием асимптотической устойчивости
схемы (3)
является
условием асимптотической устойчивости
схемы (3)

Если
 явная
схем устойчива асимптотически при
явная
схем устойчива асимптотически при
 .
При
.
При
 чисто
неявная схема асимптотически устойчива
чисто
неявная схема асимптотически устойчива
 .
При
.
При
 асимптотически
устойчива при
асимптотически
устойчива при





