35. Устойчивость многошагового метода по начальным данным.
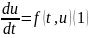
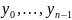– заданы.
,
где
– точное решение в точке
Уравнение для погрешности
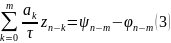
где невязка
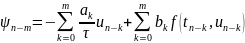
Необходимо исследовать уравнение (3)
Рассмотрим однородное разностное уравнение:
Уравнение
(4) устойчиво
по начальным данным, если
∃
:
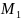∀ начальных данных
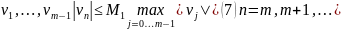
Ищем
частные решения уравнения (4) в виде
,
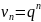
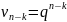k=0…m
=>
– характеристическое
уравнение, соответствующее (4)
Выполнимо
условие
корней,
если все корни
характеристического уравнения (6) лежат
внутри или на границе единичного круга,
причем на границе нет кратных корней.
ТЕОРЕМА. Условие корней необходимо и достаточно для устойчивости уравнения (4) по начальным данным.
ДОК-ВО:
Необходимость.
Пусть уравнение (4) имеет корень q : |q|>1.
Зададим
в качестве начальных данных
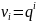, i=0,…,m-1
=>
решение , n≥m неограниченно растет при n→∞ => невозможна оценка вида (7) для точного решения => условие | |≤1 необходимо для устойчивости.
Достаточность.
,
n=m,m+1,…
S=
;
det S =
=
=
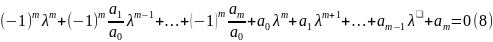
где λ – собственное значение матрицы S. Множество S совпадает с множеством корней характеристического уравнения (6).
ЛЕММА.
Если выполнено условие корней =>∃
норма
ДОК-ВО:
С помощью преобразования подобия
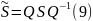приведем к жордановой форме
,
,
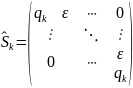где
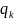– собственное значение для S,
.
,
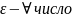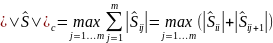где
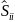совпадает с одним из
корней характеристического уравнения
Если
=>
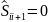по условию Леммы
Если
=>
При
достаточно малом ε
=>
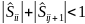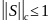
Введем
норму
,
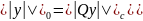где Q
определенно из (9) =>
.
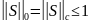ДОК-ВО ТЕОРЕМЫ:
Из (10) с учетом Леммы =>
=>
∀
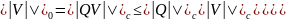
невырожденного QV=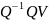
=>
=>
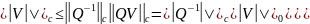
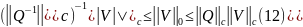
из (11,12)
,
где
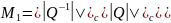
из
(13) =>
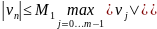
=> уравнение (4) устойчиво по начальным данным.
36. Оценка решения неоднородного разностного уравнения. Устойчивость многошагового метода по правой части.
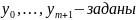
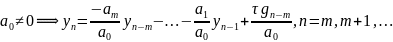
Если однородное уравнение устойчиво по начальным данным, то для неоднородного справедлива оценка:
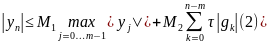
Выполнение (2) означает по определению устойчивость уравнения (1) по правой части. => из устойчивости по начальным данным следует устойчивость по правой части.
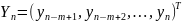
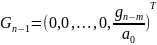
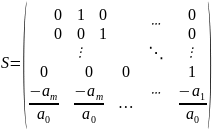
Пусть
однородное уравнение устойчиво по
начальным данным. => Выполняется условие
корней =>∃
норма
=>
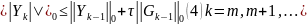
Просуммируем
(4) по k=
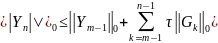
Используем
неравенство
=>
=>
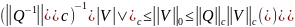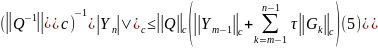
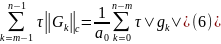
Из
(5,6) =>
где
,
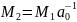
Q – матрица перехода S к жордановой форме
(7) – оценка решения неоднородного уравнения.
ТЕОРЕМА.
Пусть выполнимо условие корней. Пусть
=>
=>
при τ≤
для решения уравнения
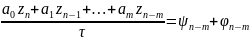(8) ,
n=m,m+1,…
справедлива
оценка
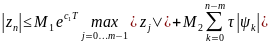(9) n=m,m+1,…
,
,
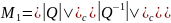L
,
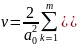
ДОК-ВО:
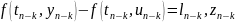, где
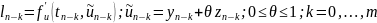
Подставим (10) в уравнение (8):
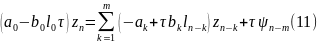
Из
условия τ≤
=>
уравнение
(11) можно разрешить относительно
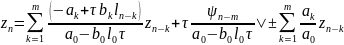
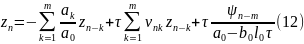где
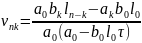
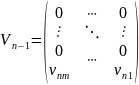
Уравнение
(12) эквивалентно
∃
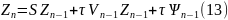
норма
=>
=>
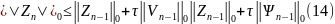
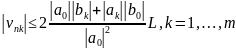
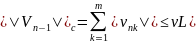
где
=>
=>
(14) переходит в
=>
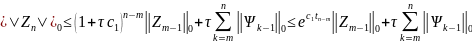
где
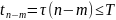
Используя
(*,**) =>
=>
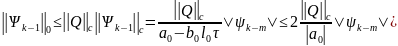
37. Разностная аппроксимация Пуассона. Порядок аппроксимации
Рассмотрим
при
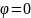
В
области G
введем равномерную сетку
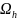
Заменим частные производные разностными:
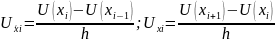
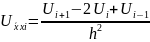
Задачу (1) в разностном приближении можно записать в виде:
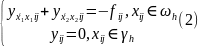
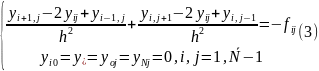
Уравнений
и неизвестных по
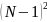
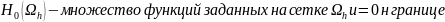
Введем скалярное произведение:
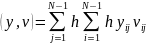
A-оператор,
действующий на сеточную функцию
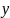
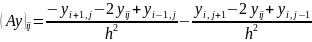
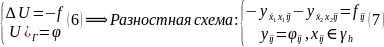
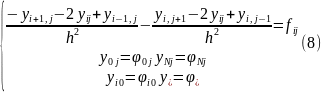
Задачу
(7),(8) можно свести к задаче с однородными
граничными условиями, заменив правые
части
в приграничных точках
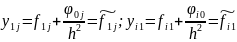
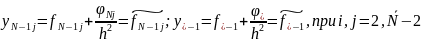
А в остальных точках:
Получаем
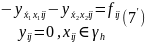
Порядок аппроксимации
Пусть
-
решение задачи Дирихле (6), а
-
решение разностной задачи (8). Рассмотрим
погрешность
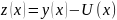
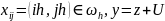
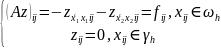
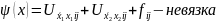
Где
=> 2 порядок аппроксимации