26. Решение нелинейных уравнений методом простых итераций, релаксации. Сходимость метода релаксации.

Пусть задана функция действительного переменного. Требуется найти корни уравнения

(1).

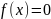
или, что то же самое, нули функции .

Не существует каких-то общих регулярных приемов решения задачи о расположении корней произвольной функции . Наиболее полно изучен вопрос о расположении корней алгебраических

многочленов

(2).

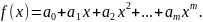
Численные методы решения нелинейных уравнений являются, как правило, итерационными методами, которые предполагают задание достаточно близких к искомому решению начальных данных.

Метод простой итерациисостоит в том, что уравнение (1) заменяется эквивалентным уравнением

(3).

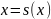
и итерации образуются по правилу

(4).

причем задается начальное приближение .

Для сходимости метода большое значение имеет выбор функции , которую можно задавать различными способами, однако обычно она берется в виде

(5). ,

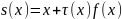причём функция не меняет знака на том отрезке, где отыскивается корень.

При надлежащем выборе значения метод простой итерации сходится, если 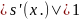, где - корень уравнения (1).

Если 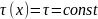, то получим метод релаксации:

(6).

для которого , и, метод сходится при условии

(7).

Если в некоторой окрестности корня выполняются условия

(8). ,

то метод релаксации сходится при

Чтобы выбрать оптимальный параметр в методе релаксации, рассмотрим уравнение для погрешности

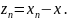
Подставляя 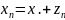в (6), получим уравнение:

.

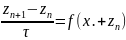По теореме о среднем имеем:

, где .

Таким образом, для погрешности метода релаксации выполняется уравнение:

.

Отсюда приходим к оценке:

,

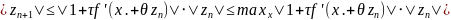и, если выполнены условия (8), то

Таким образом, задача выбора оптимального параметра сводится к нахождению , для которого функция

принимает минимальное значение.

Из рассмотрения графика функции видно, что точка минимума определяется условием

и равна

При этом значении имеем:

так что для погрешности справедлива оценка

27. Сходимость метода простых итераций

Теорема о сходимости. Перепишем уравнение

(1).

в эквивалентном виде

(2).

и рассмотри метод простой итерации

(3). - задан

Говорят, что итерационный метод сходится, если последовательность имеет предел при .

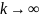В следующей теореме формулируются условия на функцию , гарантирующие существование и единственность решения уравнения (2) и сходимость метода простой итерации к этому решению. Напомним, что функция называется Липшиц-непрерывной с постоянной на множестве 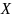, если для всех выполняется неравенство

(4).

В дальнейшем в качестве X будем брать отрезок длины c серединой в точке .

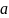(5).

Теорема 1. Если Липшиц-непрерывна с постоянной 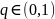на отрезке 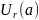, причем

(6). ,

то уравнение (2) имеет на отрезке единственное решение , и метод простой итерации (3) сходится к при любом начальном приближении . Для погрешности справедлива оценка

(7).

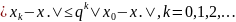
Доказательство. Сначала докажем по индукции, что , т.е., что метод простой итерации не выводит за пределы того множества, на котором Липшиц-непрерывна с постоянной . Предположим, что при некотором , и докажем, что тогда .

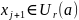Из равенства

получим

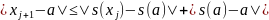
Учитывая условие липшиц-непрерывности, предположение индукции и условие (6), имеем

, т.е. .

Оценим теперь разность двух соседних итераций . Имеем

и поскольку все точки находятся на отрезке , получаем оценку

и, следователдьно,

(8).

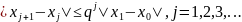
Оценка (8) позволяет доказать фундаментальность последовательности . Действительно, пусть р — любое натуральное число. Тогда

,

и согласно (8) имеем

,т.е.

(9).

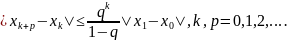
Поскольку правая часть неравенства (9) стремится к нулю при и не зависит от , последовательность является фундаментальной. Следовательно, существует

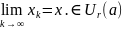
Переходя в (3) к пределу при и учитывая непрерывность функции , получим

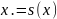, т. е. — решение уравнения (2).

Предположим, что 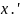— какое-то решение уравнения (2), принадлежащее отрезку . Тогда

и по условию теоремы

Так как 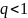, последнее неравенство может выполняться лишь при 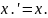т. е. решение единственно.

Докажем оценку погрешности (7). Из уравнения (3) получим

,

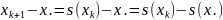и так как , приходим к неравенству

(10).

справедливому для всех , из которого и следует оценка

(7). Теорема 1 доказана.

Замечание 1. По теореме о среднем, для выполнения (4) достаточно (12). где, (12) это

Замечание 2. Если - решение (2) и в уравнение (2) не имеет других решений и метод (3) сходится, если .

Доказательство. Поскольку непрерывно дифференцируема на отрезке и , найдутся числа и , такие что

для всех .