24. Апостерионная оценка погрешности методом Рунге. Автоматический выбор шага интегрирования.

Величина погрешности численного интегрирования зависит как от шага сетки , так и от гладкости подынтегральной функции 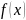. Если величина погрешности велика, то ее модно уменьшить путем измельчения сетки на данном отрезки 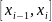. Для этого прежде всего надо уметь апостериорно, т. е. после проведения расчета, оценивать погрешность.

Апостериорную оценку погрешности можно осуществить методом Рунге, который мы выясним сначала на примере формулы трапеций. Пусть отрезок разбит на частичные отрезки , , , , имеющие длину . На каждом частичном отрезке применяется формула трапеций. 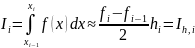где ,

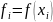Согласно (11) имеем (20) где константа зависит от гладкости и заранее неизвестна. Измельчим на отрезке сетке в два раза и повторим расчет с шагом h. Тогда согласно (20) будем иметь Из соотношений (20), (21) можно исключить константу и получить оценку погрешности, которая содержит лишь известные величины

Метод Рунге можно применять и для оценки погрешности других квадратурных формул. Пусть какая-то квадратурная формула имеет на частичном отрезке порядок точности , т. е. . Тогда откуда получим 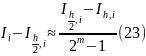Возможность апостериорно оценивать погрешность позволяет вычислять интеграл с заданной точностью путем автоматического выбора шага интегрирования . Пусть используется составная квадратурная формула где – квадратурная сумма на частичном отрезке, причем на каждом частичном отрезке используется одна и та же квадратурная формула (например, формула трапеций Симпсона и др.). Проведем на каждом частичном отрезке все вычисления дважды, один раз – с шагом и второй раз – с шагом и оценим погрешность по правилу Рунге (23).

Если для заданного будут выполняться неравенства то получим т. е. будет достигнута заданная точность . Если же на каком-то из частичных отрезков оценка (24) не будет выполняться, то шаг на этом отрезке надо измельчить еще в два раза и снова оценить погрешность. Измельчение сетки на данном отрезке следует проводить до тех пор, пока не будет достигнута оценка вида (24). Заметим, что для некоторых функций такое измельчение может продолжаться слишком долго. Поэтому в соответствующей программе следует предусмотреть ограничение сверху на число измельчений, а также возможность увеличения .

Таким образом, автоматический выбор шага интегрирования приводит к тому, что интегрирование ведется с крупным шагом на участках плавного изменения функции и с мелким шагом – на участках быстрого изменения . Это позволяет при заданной точности уменьшить количество вычислений значений по сравнению с расчетом на сетке с постоянным шагом. Подчеркнем что для нахождения сумм не надо пересчитывать значения во всех узлах достаточно вычислять только в новых узлах.

25. Численное дифференцирование. Связь между точностью вычисления функции и шагом сетки.

Пусть на [a,b] задана функция u(x) и сетка 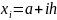. Можно ввести первую производную:

• с шагом назад:

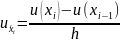
• с шагом вперед:

• центрально-разностная:

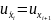
Оценим порядок точности:

,

,

Получаем ,

Т.о. 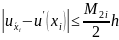, , 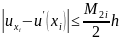где ,

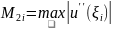Т.е. , где ,

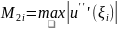Вторую производную в точке можно определить как

Используя разложения и до 4-го порядка, получим

. Т.о. , ,

Пусть u(x) задана приближенно, т.е. вместо берем , , .

Пусть . Если точность вычислений зафикс-на, а h убывает, то разница может сколь угодно возрастать, поэтому операцию численного дииф-я наз-ют некорректной.

Т.о.

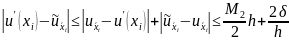
Чтобы разница была минимальной, приравниваем:

Т.о. если h зафиксировано, то берем

Если зафиксировано , то берем

Получаем