22. Наилучшее приближение в гильбертовом пространстве.
Пусть в линейном гильбертовом пространстве H задана конечная л.н.з. система элементов:
(1)
.
Требуется приблизить элемент f
H
линейными комбинациями заданных функций.
Обозначим
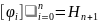- множество линейных комбинаций.
Рассмотрим задачу о наилучшем приближении,
состоящую в том, чтобы для заданного f
H
среди всех линейных комбинаций найти
такой обобщенный многочлен
,
для которого отклонение
(/*было
бы минимальным. Под H понимается
*/).
Элемент
,
дающий решение этой задачи, наз. элементом наилучшего приближения.
Рассмотрим
.
Пусть матрица
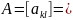и
векторы
,
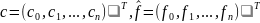где
.
Введем скалярное произведение
.
Тогда уравнение (3) можно записать в виде
(4)
Полагаем
,
(5)
.
Таким
образом задача о нахождении наилучшего
приближения в гильбертовом пространстве
Н сводится к минимизации функционала
(6)
,
определенного на множестве вещественных
(п+1)-мерных векторов. Отметим основные
свойства матрицы А.
1) А
—симметричная матрица, поскольку
.
2) А>0—
положительно определенная матрица. Из
(5) следует, что
.
Предположим, что
.
Тогда
.
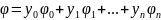Имеем,
что
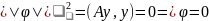
, что означает, что вектора л.з., противоречие.
Теорема.
Пусть А - симметрическая, положительная
определенная матрица и
-
заданный вектор. Тогда функционал (6)
имеет единственную точку минимума
.
Вектор
тогда и только тогда минимизирует
функционал (6), когда
является решением уравнения (7)
.
Док-во.
Заметим, что система (7) имеет единственное
решение, поскольку А — положительно
определенная матрица (det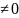
,
имеет обратную). Пусть
- решение ур. (7). Рассмотрим для
произвольного
вектора v:
.
,
что означает, что
- точка минимума функционала F(
).
В другую сторону. Пусть минимизирует функционал (6). Тогда учитывая проведенные выше преобразования, находим, что
(/*обозначение).
Поскольку — точка минимума функционала F( ), при любых y и выполняется неравенство
,
т.е.
.
Таким образом,
=0
является точкой минимума g(
)
и, след-но,
g'(
)=0.
Отсюда получаем, g'(
)=
что и в силу произвольности вектора y
приходим к выводу, что
,
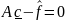т.е. выполнено условие (7). Теорема
доказана.
Алгоритм построения элемента наилучшего приближения в гильбертовом пространстве состоит в следующем: 1) вычисление элементов , k,l=0...n матрицы А;
2) вычисление правых частей
,
где
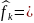,k,l=0...n
3) решение системы уравнений
4) вычисление суммы
.
Лемма. Если
— элемент наилучшего приближения в Н
вектора f, то
,
т.е. погрешность
ортогональна элементу наилучшего
приближения
.
или
.
Док-во. Пусть
- элемент наилучшего приближения вектора
f. Тогда
в (n+1) -мерном пространстве. С другой
стороны, в силу (5)
.
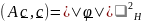Т.о.
=
.
Утверждение будет доказано, если мы
покажем, что
=
.
,
таким образом лемма доказана.
Следствие. Если — элемент наилучшего приближения в Н вектора f, то
Док-во.
,
так как
Рассмотрим случай, когда система {
}
ортонормированная, т.е.
.
Тогда А=Е и ур. (7) принимает вид
,
т.е.
и имеет место оценка
и
23. Численное интегрирование. Формула прямоугольника, трапеции, Симпсона. Оценка погрешности.
Рассмотрим способы приближенного вычисления определенных интегралов
(1),
основанные на замене интеграла конечной суммой
(2),
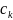— числовые коэффициенты и
— точки отрезка [a, b], k =0...n.
называется квадратурная формула (в
многомерн.сл. -куботурная ф-ла), точки
наз. узлами квадратурной формулы, а
числа
-
коэффициентами квадратурной формулы.
Разность
называется погрешностью квадратурной формулы. Погрешность зависит как от расположения узлов, так и от выбора коэффициентов.
(3)
,
(4)
введена
равномерная сетка с шагом h, т.е. множество
точек
Для построения
формулы на всем [a,b] достаточно построить
квадратурную формулу для
на частичном отрезке
и
воспользоваться свойством (3).
/*первая куботурная ф-ла - это ф-ла прямоугольников
Формула прямоугольников.
Заменим интеграл
(4) выражением
,
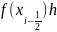где
;
Тут рисунок, Шериф=))))))
Геометрически это означает, что площадь криволинейной трапеции ABCD заменяется площадью прямоугольника ABCD'. Тогда получим формулу
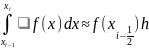(5)
которая называется формулой
прямоугольников на частичном отрезке .Погрешность определяется величиной
которую легко оценить с помощью формулы
Тейлора.
Воспользуемся
разложением Тейлора ф-и f в окрестности
точки
:
.
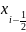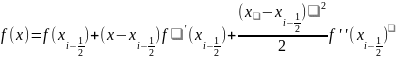Замена f
.
Подставим в интеграл и получим
/*и еще
,
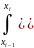
где
.
Составная
формула прямоугольников
,
получена суммированием по i р-ва (5)
Погрешность
равна сумме погрешностей по всем
частичным отрезкам и так как
,
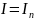то
где
т. е. погрешность
формулы прямоугольников на всем отрезке
есть величина O(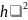
).
/*В этом случае говорят, что квадратурная формула имеет второй порядок точности.
Формула трапеции
На частичном
отрезке эта формула имеет вид
и получается путем замены подынтегральной
функции f(x) интерполяционным многочленом
первой степени, построенным по узлам
,
т. е. функцией
Для оценки
погрешности достаточно вспомнить, что
Отсюда получим
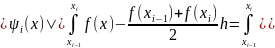
и, следовательно,
.
Оценка неулучшаема, так как в ней
достигается равенство, например, для
.
Составная формула трапеций имеет вид
Погрешность этой формулы оценивается следующим образом:
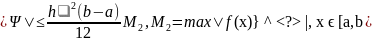
Таким образом,
формула трапеций имеет, так же как и
формула прямоугольников, второй порядок
точности,
,
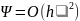но ее погрешность оценивается величиной
в два раза большей.
Формула Симпсона
На [
вводим
среднюю точку: [
.
При аппроксимации
интеграла (4) заменим функцию f(x) параболой,
проходящей через точки
,
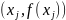j=i-1, i-0.5, i, т. е. представим приближенно
f(x) в виде
.
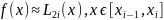где
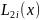—интерполяционный
многочлен Лагранжа 2ой степени
Построим
многочлен Лагранжа
по точкам
:
/*
Таким образом,
приходим к приближенному равенству
,
которое называется формулой Симпсона
или формулой парабол.
Квадратурную
формулу полагаем в виде
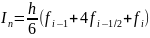
На всем отрезке [а, Ь] формула Симпсона имеет вид
,
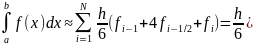где
.
Обозначим
,
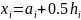i=0..2N ,чтобы не использовать дробных
индексов, и запишем формулу Симпсона в
виде
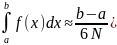/*число точек 2N
Прежде чем
переходить к оценке погрешности формулы
Симпсона заметим, что она является
точной для любого многочлена третьей
степени, т. е. имеет место точное равенство
если
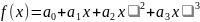/*чтобы доказать, нужно отдельно проверить
для x=1,
x=1:
x=x:
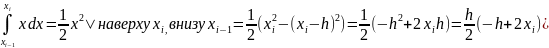
Далее, положим,
что
;
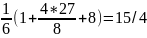чтд
;
чтд
Введем многочлен
:
;
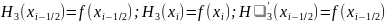//пользуемся
интерполяц. мнгч Эрмита
Тогда т.к. формула Симпсона верна для любого многочлена третьей степени, то
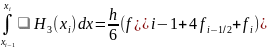
Обозначим
-погрешность интерполирования мнгч
Эрмита. Тогда
,
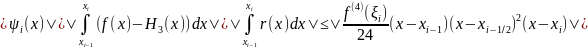
т.к.
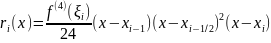
где
=sup
,
Общая погрешность:
,
=sup
,
