19. Сходимость интерполяционных процессов. Интерполяция с кратными узлами.

Сходимость интерполяционных процессов.

Будет ли стремиться к нулю погрешность интерполирования 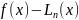, если число узлов неограниченно увеличивать? Ответ, вообще говоря, отрицательный.

Сформулируем определение сходимости интерполяционного процесса. Множество точек , таких, что

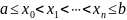
назовем сеткой на отрезке и обозначим через . До сих пор предполагалось, что число узлов интерполяции фиксировано. Пере­ходя к изучению сходимости интерполяционного процесса, необходимо рассмотреть последовательность сеток с возрастающим числом узлов, а именно последовательность

Пусть функция определена и непрерывна на . Тогда можно задать последовательность интерполяционных многочленов 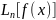, построенных для функции по ее значениям в узлах сетки .

Говорят, что интерполяционный процесс для функции сходится в точке 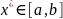, если существует

.

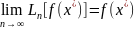Кроме поточечной сходимости рассматривается сходимость в различных нормах. Например, равномерная сходимость на отрезке [a, b] означает, что

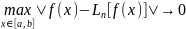
при

Свойство сходимости или расходимости интерполяционного процесса зависит как от выбора последовательности сеток, так и от гладкости функции .

Известны примеры несложных функций, для которых интерполяционный процесс расходится. Так, последовательность интерполяционных многочленов, построенных для непрерывной функции по равноотстоящим узлам на отрезке [-1, 1], не сходится к функции ни в одной точке отрезка [-1, 1], кроме точек -1, 0, 1.

Более общее утверждение содержится в

Теорема Фабера.

Какова бы ни была последовательность сеток 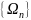найдется непрерывная на функция такая, что последовательность интерполяционных много­членов не сходится к равномерно на отрезке .

Для заданной непрерывной функции можно добиться сходимости за счет выбора расположения узлов интерполяции. Справедлива

Теорема Марцинкевича.

Если непрерывна на , то найдется такая последовательность сеток, для которой соответствующий интерполяционный процесс сходится равномерно на .

Интерполяция с кратными узлами.

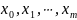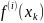В узлах , среди которых нет совпадающих узлов, заданы значения функции и ее производных до порядка включительно, . Таким образом, в каждой точке 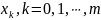, известны

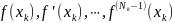
и, следовательно, всего известно 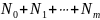величин. Требуется построить алгебраический многочлен степени для которого

. (1)

Многочлен , удовлетворяющий условиям (1), называется интерполяционным многочленом Эрмита для функции 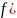. Число 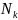называется кратностью узла .

Докажем, что интерполяционный многочлен Эрмита существует и единствен. Условия интерполяции (1) представляют собой систему линейных алгебраических уравнений относительно коэффициентов 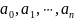многочлена

.

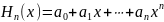Число уравнений этой системы равно числу неизвестных и равно . Поэтому достаточно показать, что однородная си­стема

, (2)

имеет только тривиальное решение .

Группа условий (2) при фиксированном и означает, что число является корнем кратности многочлена . Таким образом, многочлен имеет всего с учетом кратности не менее корня на . Поскольку степень равна , этот многочлен тождественно равен нулю, следовательно, равны нулю его коэффициенты и однородная система уравнений (2) имеет единственное решение . Неоднородная система (1) однозначно разрешима при любых правых частях.

Поскольку значения 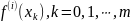, входят только в правую часть системы (1), коэффициенты 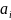мно­гочлена выражаются линейно через значения , и этот многочлен можно представить в виде линейной комбинации

,

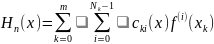где — многочлены степени и

Верна оценка погрешности интерполирования: