32. Необходимые и достаточные признаки точки перегиба.

Точки перегиба 

     Пусть функция f определена в некоторой окрестности точки x₀, непрерывна в точке x₀ и имеет в этой точке конечную или бесконечную производную. Если при переходе через точку x₀ функция f меняет направление выпуклости, то x₀ называют точкой перегиба функции f, а точку (x₀; f(x₀)) - точкой перегиба графика функции f. График функции переходит с одной стороны касательной, проведенной в точке (x₀;f(x₀)), на другую сторону. Точки перегиба f - точки экстремума для f'.

     Необходимые условия наличия перегиба 

       либо   не существует.

     Достаточные условия наличия перегиба 

     1. Если   меняет знак при переходе через точку x₀, то x₀ - точка перегиба.

     2. Если   то при n четном x₀ - точка перегиба, при n нечетном x₀ не является точкой перегиба.

33. Асимптоты

Асимптоты графика функции

Асимптотой графика функции у = f(x) называется прямая, расстояние от которой до текущей точки графика функции стремится к нулю при неограниченном удалении этой точки от начала координат. Для нахождения вертикальных асимптот, то есть асимптот, параллельных оси OY, надо найти точки разрыва функции I I рода. Если х0 – такая точка, то хотя бы один из пределов  f(x) или  f(x) равен бесконечности. Это означает, что прямая х = х0 – вертикальная асимптота. Если функция не имеет точек разрыва II рода, то график функции не имеет вертикальных асимптот. Пусть график функции y = f(x) имеет невертикальную асимптоту. Уравнение невертикальной прямой можно записать в виде y = kx+b. Пусть М(х,у) – текущая точка графика. Опустим из точки М перпендикуляр МN на асимптоту. Из определения асимптоты следует:  MN = 0. Из ∆М1MN получаем М1М =  , где  – угол между асимптотой и осью ОХ. Поскольку  – величина постоянная, то  . Заметим, что М1М = РМ1-РМ = уасимпт.-уграфика = (kx+b)-f(x), поэтому   Последнее равенство означает, что функция   является бесконечно малой при  . Разделим обе части последнего равенства на х и перейдем к пределу при  , получим  . Так как  Определим теперь b. Так как   то   Переходя к пределу при  , получаем Если k или b не существуют, то график функции не имеет невертикальной асимптоты. В частном случае при k = 0 получается горизонтальная асимптота. Аналогично находят асимптоты при x . График может иметь различные асимптоты при  и x  или иметь только одну из них.

34. Понятие производной, физич. и геом. ее смысл.

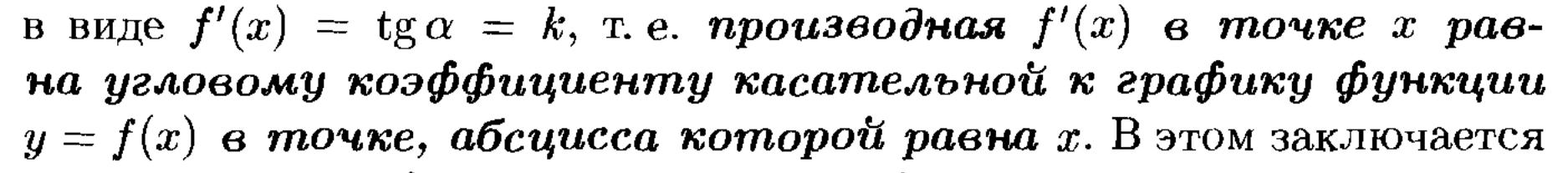
35. Таблица производных элементарной функции.

36. Производная суммы, разности, произведения и частного функций.

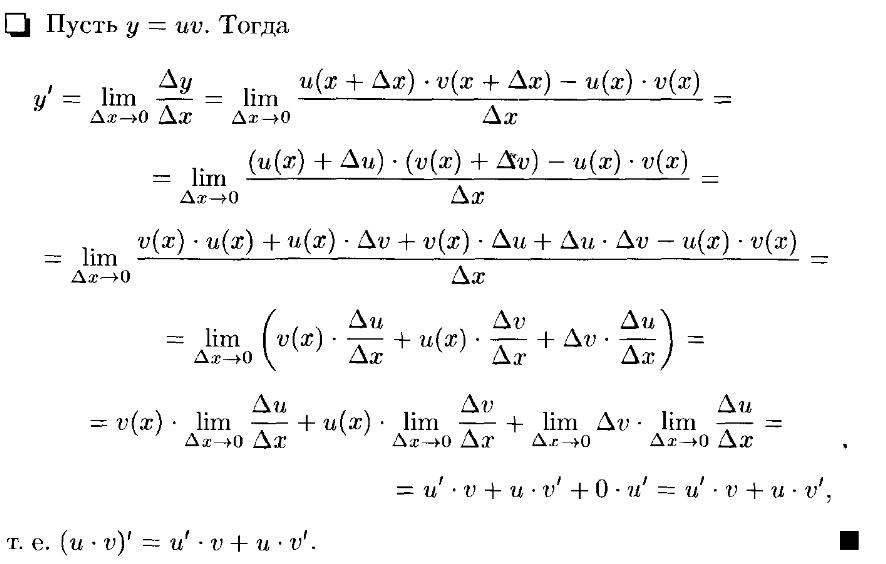
37. Дифференциал функции. Его применение для приблизительных расчетов.

38. Общая схема построения графика функции.

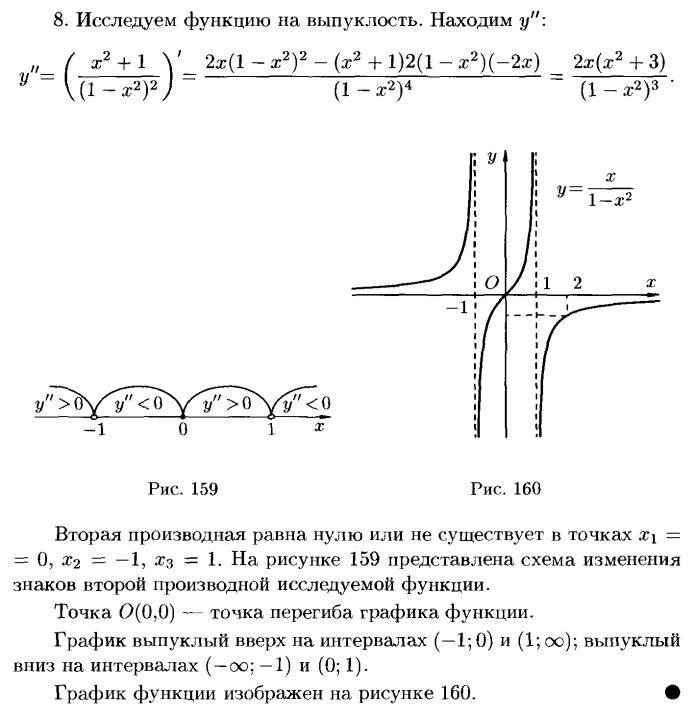
39. Дифференцирование функций, заданных неявно, параметрически и сложных функций.

НЕЯВНАЯ

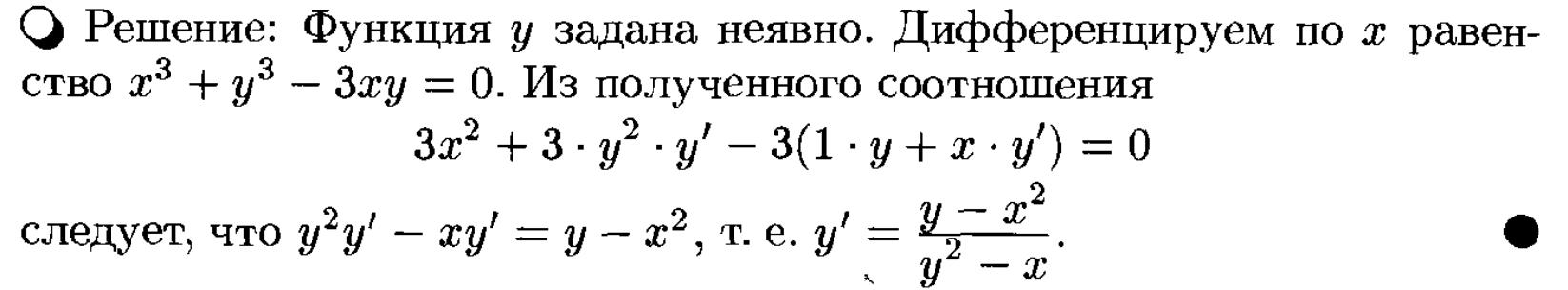
ПАРАМЕТРИЧЕСКАЯ

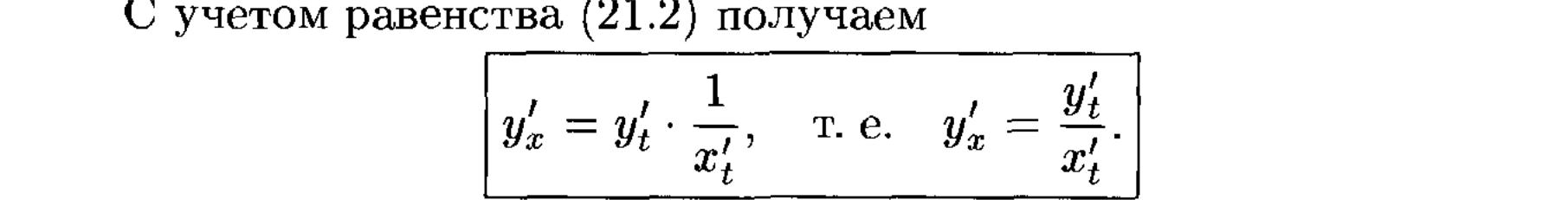
СЛОЖНАЯ

40. Уравнение касательной и нормали к прямой.

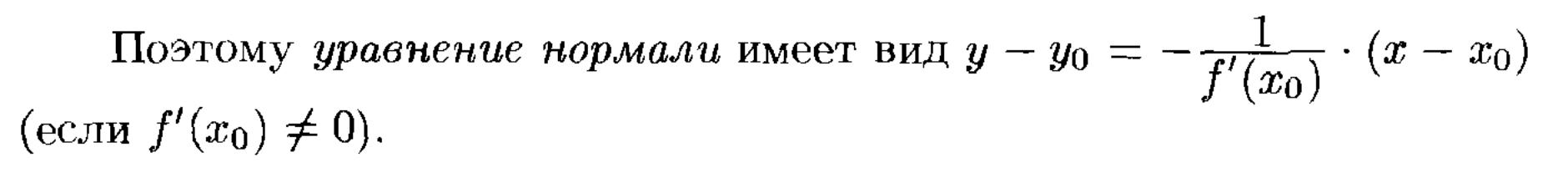
41. Необходимый и достаточный признак монотонности функции.

Определение. Функция называется возрастающей в интервале, если большему значению аргумента соответствует большее значение функции.

 Функция называется убывающей в интервале, если большему значению аргумента соответствует меньшее значение функции.

Интервал, где функция возрастает, называется интервалом возрастания функции.

Интервал, где функция убывает, называется интервалом убывания функции. Эти интервалы называются интервалами монотонности функции.

Применим понятие производной к исследованию функции на монотонность. Необходимые и достаточные условия монотонности функции устанавливают теоремы:

Теорема 1. (необходимый признак монотонности)

1)                 Если функция   в интервале возрастает, то её производная   для х, принадлежащих этому интервалу.

2)                 Если функция   в интервале убывает, то её производная   для х, принадлежащих этому интервалу.

3)                 Если функция   в интервале не изменяется, то её производная   для х, принадлежащих этому интервалу.

Теорема 2. (достаточный признак монотонности)

1)                 Если для функции f(x) её производная  >0 в некотором интервале, то f(x) в этом интервале возрастает.

2)                 Если для функции f(x) её производная  <0 в некотором интервале, то f(x) в этом интервале убывает.

3)                 Если для функции f(x) её производная   в некотором интервале, то f(x) в этом интервале не изменяется.

Эти две теоремы выражают следующий геометрический факт: если на [a,b] функция возрастает, то касательная к кривой в каждой точке этого отрезка образует с осью ОХ острый угол   или в отдельных точках – горизонтальна, tg0.

 

 

 

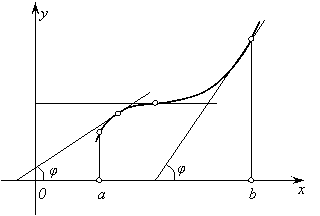
Рис. 30.

 

Если на [a,b] функция f(x) убывает, то касательная к кривой в каждой точке этого отрезка образует с осью ОХ тупой угол  или в отдельных точках горизонтальна, tg≤0.

 

 

Рис. 31.