30. Достаточные признаки экстремума.

Определение 4. Точки, которых производная функции обращается в нуль, называются стационарными точками функции (см. рис. 1.4, точки и ).

Определение 5. Точки, которых производная функции не существует, но в них определена, называются критическими точками функции (см. рис. 1.5, точка ).

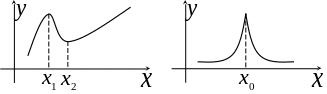
Рис. 1.4 Рис. 1.5

Каждая стационарная или критическая точка – это точка возможного экстремума функции. Однако, сделать заключение о том, что в данной точке на самом деле имеется экстемум, можно лишь на основании дополнительного исследования, которое основывается на достаточных условиях экстремума.

Теорема 2. (Достаточное условие экстремума).

Пусть функция дифференцируема всюду в некоторой окрестности точки , и пусть точка является стационарной точкой функции . Тогда, если в пределах указанной окрестности производная положительна (отрицательна) слева от точки и отрицательна (положительна) справа от точки , то функция имеет, в точке локальный максимум (минимум). Если же в пределах указанной окрестности точки производная имеет один и тот же знак слева и справа от точки , то экстремума в точке нет.

Вытекающее из теоремы 2 правило можно кратко сформулировать так: 1) если при переходе через данную стационарную точку производная меняет знак с плюса на минус (с минуса на плюс), то функция имеет в точке локальный максимум (минимум); 2) если же при переходе через данную стационарную точку с производная не меняет знака, то экстремума в точке нет.

Пример. Найти точки экстремума функции .

Поскольку , то функция имеет две стационарные точки: и . При переходе через точку производная меняет знак с плюса на минус, а при переходе через точку – с минуса на плюс. Следовательно, – точка локального максимума, а – точка локального минимума.

Теорема 3. (Второе достаточное условие экстремума)

Пусть функция имеет в данной стационарной точке конечную вторую производную. Тогда функция имеет в точке локальный максимум, если , и локальный минимум, если .

31. Наим. И наиб. Значение функции на отрезке.

Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.

Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:

1. Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.

2. Вычислить значения функции на концах отрезка при x = a, x = b.

3. Из всех полученных значений выбрать наибольшее и наименьшее.