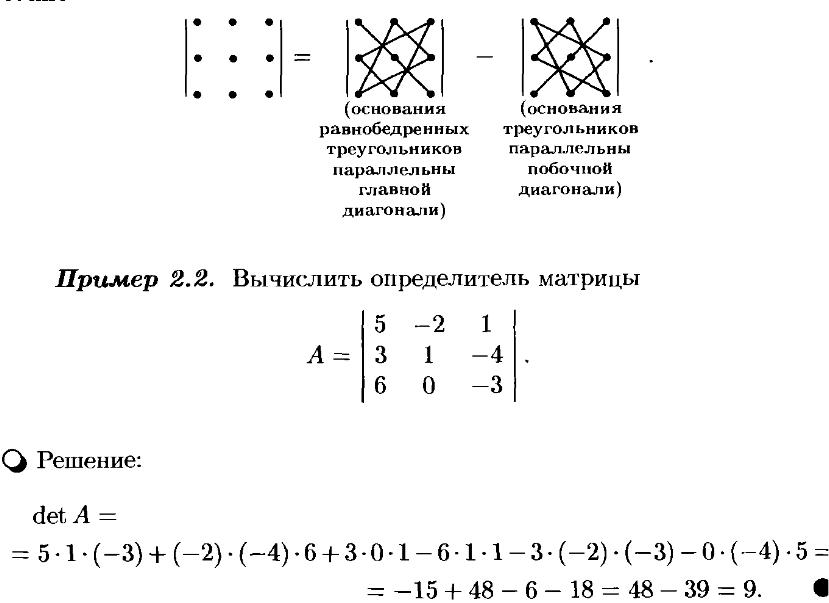
1. Определитель 2 и 3-го порядка. Их св-ва. Алгебраические дополнения. Миноры. Определитель 4 и 5-го порядка.

Порядок определителя соответствует порядку матрицы.

СВОЙСТВА для опред. любого порядка:

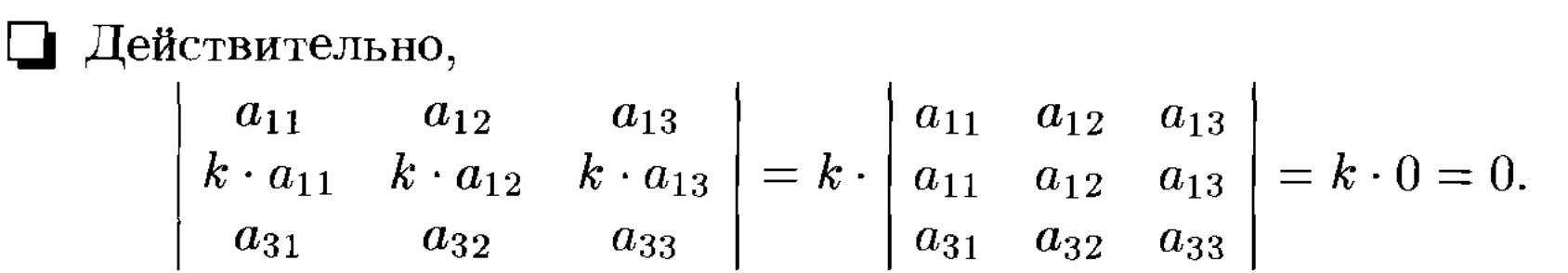
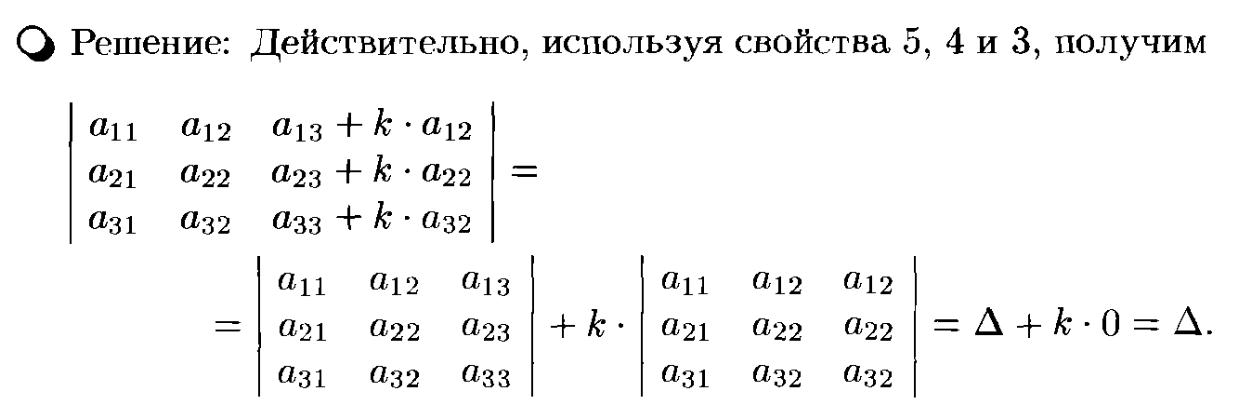
2. Матрицы. Линейные операции с матрицами.

ОПЕРАЦИИ С МАТРИЦАМИ:

3. Обратная матрица и ее нахождение.

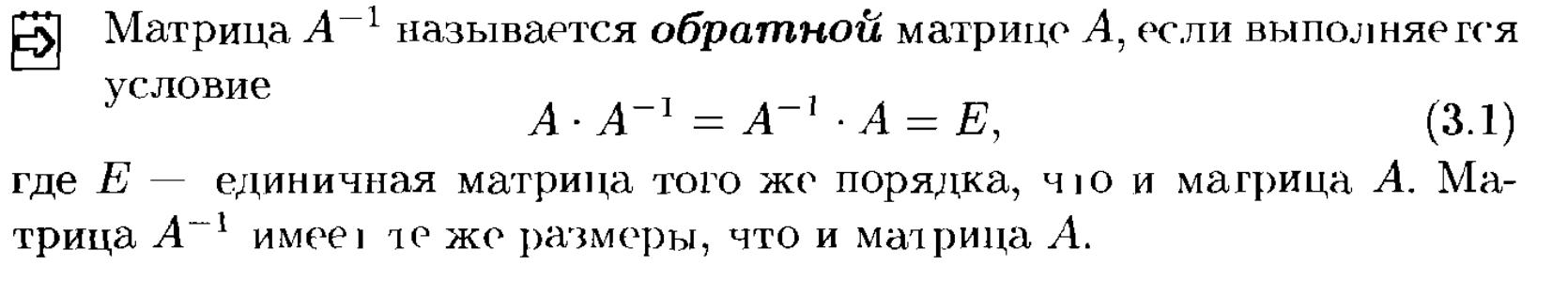
4. Ранг матрицы. Его определение с помощью эквивалентных преобразований.

5. Решение систем линейных алгебраических уравнений по формулам Крамера.

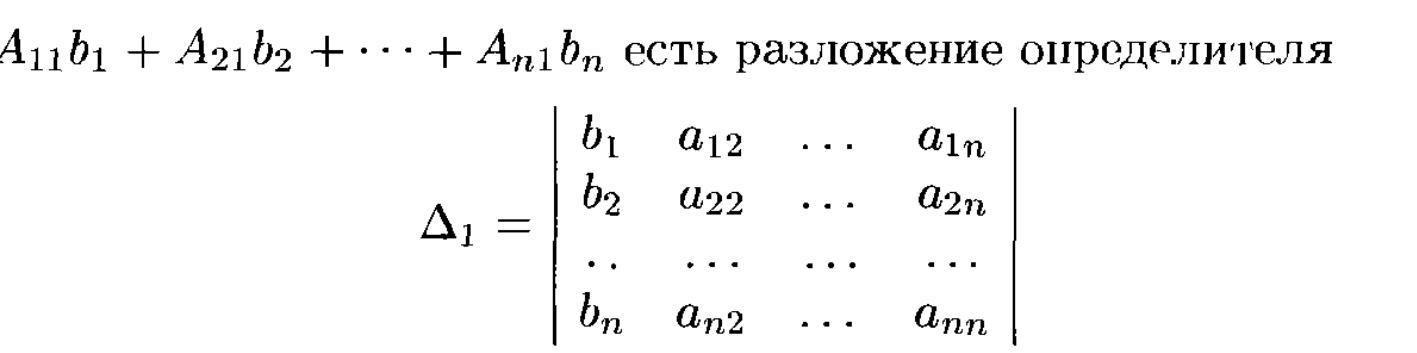
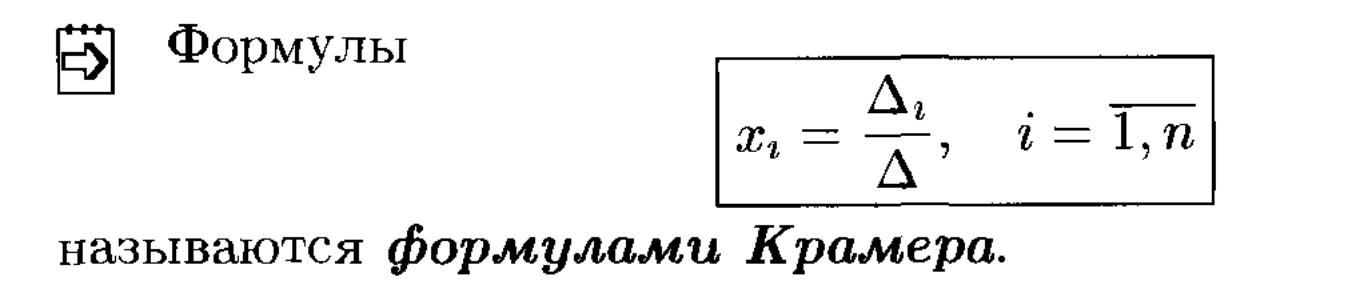
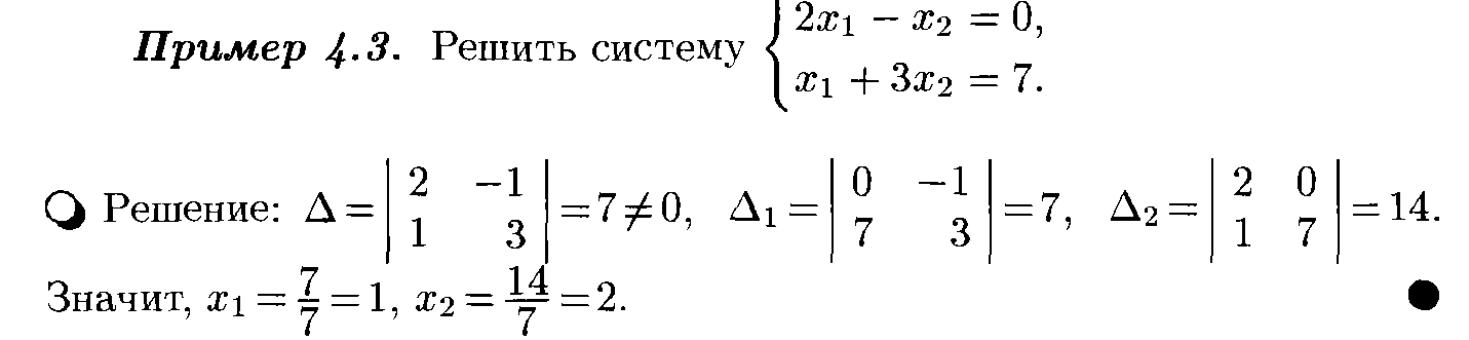
6. Решение систем линейных алгебраических уравнений матричным способом.

7. Решение систем линейных алгебраических уравнений методом Гаусса.

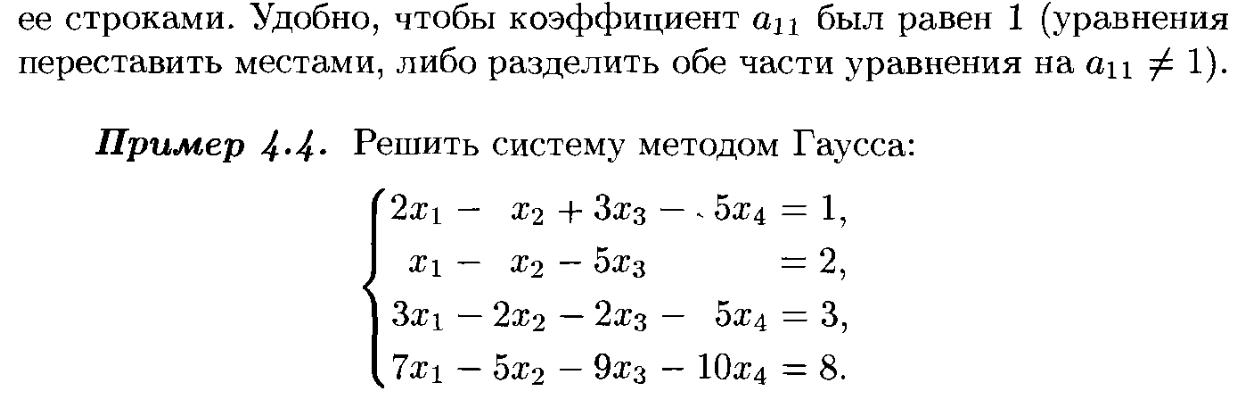
8. Теорема Кронекера-Капелли и проведение на ее основе полного исследования системы линейных уравнений.

9. Векторы и операции над ними.

ОПЕРАЦИИ НАД ВЕКТОРАМИ:

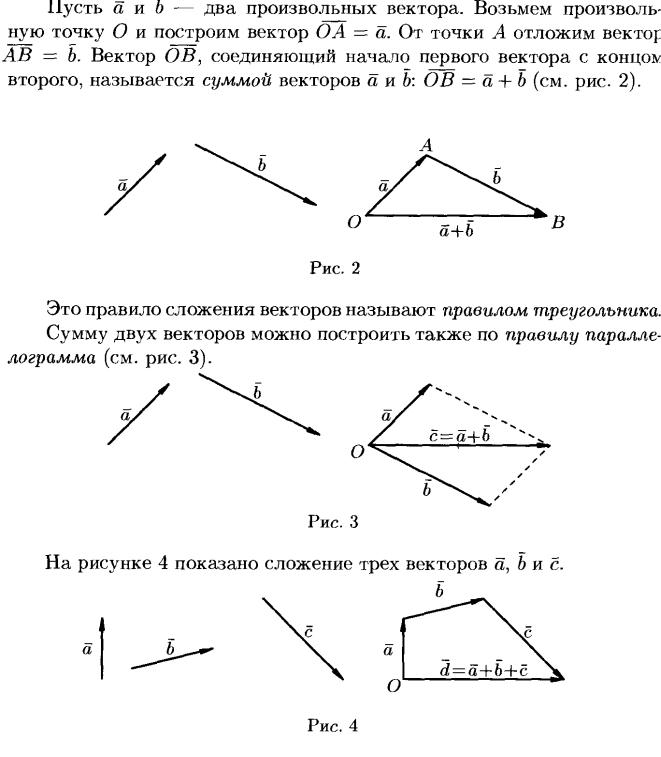
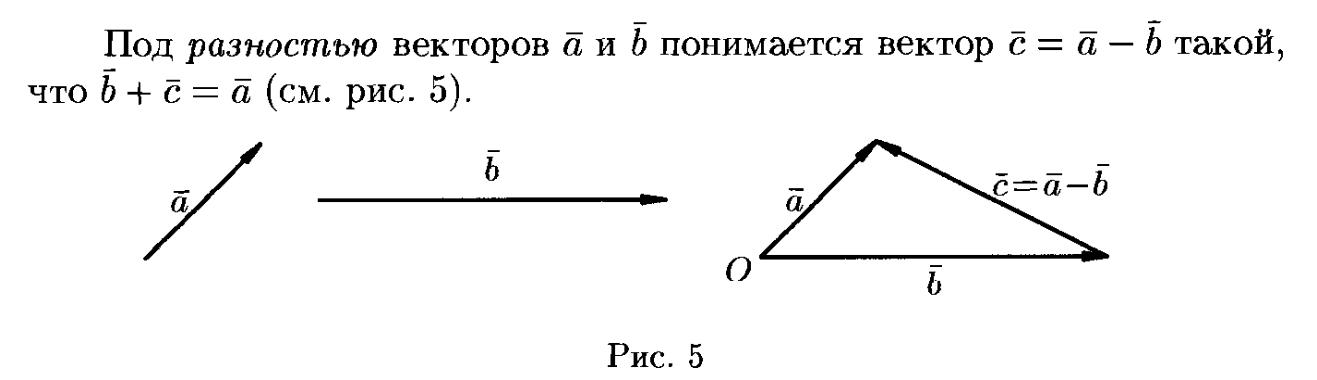
10. Скалярное и векторное произведения, их св-ва.

СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ.

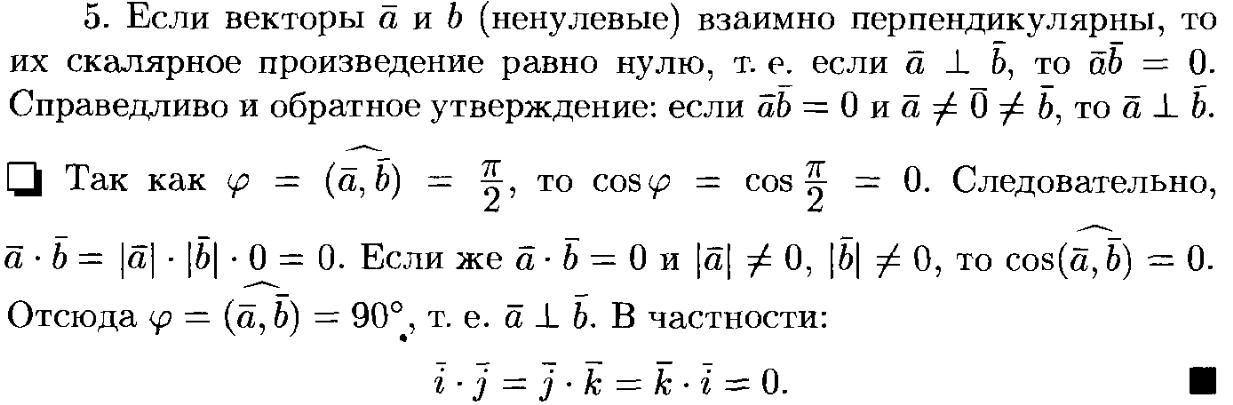
ВЕКОТРНОЕ ПРОИЗВЕДЕНИЕ.

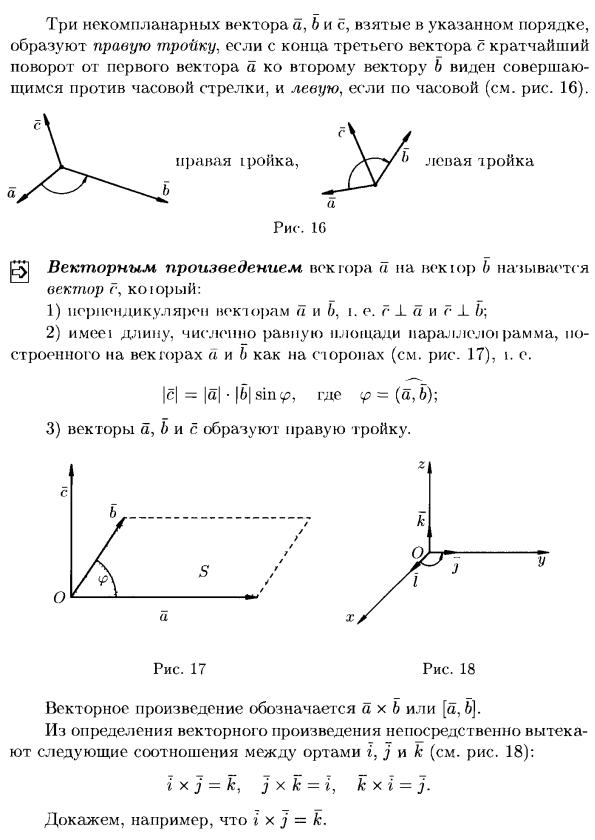
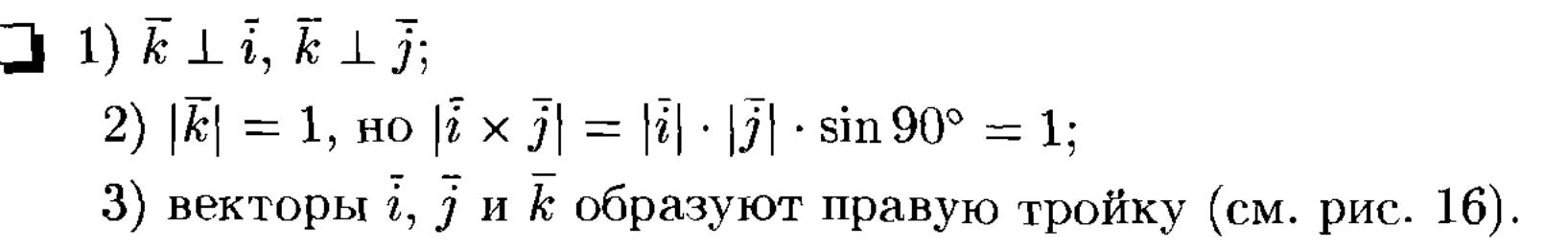
СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ.

11. Смешанное произведение векторов , его свойства (нахождение объемов параллелепипеда и пирамиды).

СВОЙСТВА СМЕШАННОГО ПРОИЗВЕДЕНИЯ

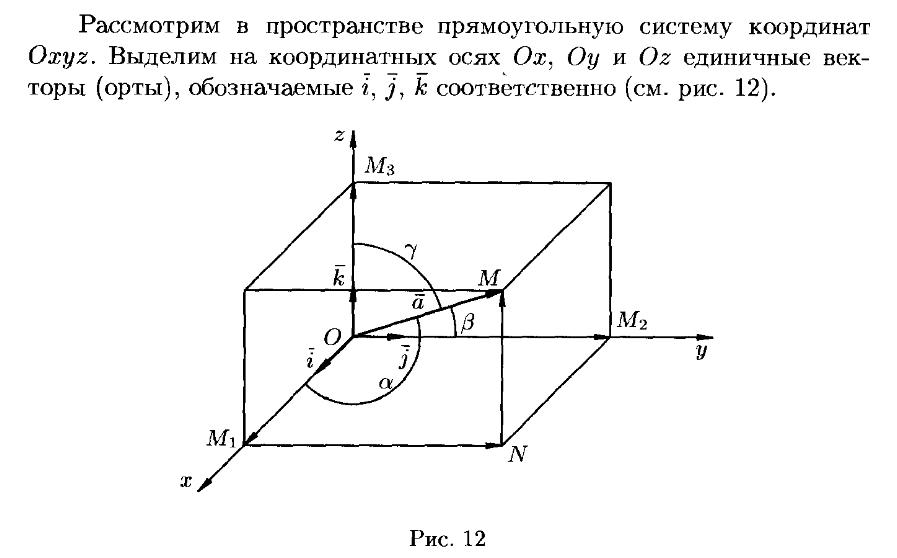
12. Разложение вектора по ортам координатных осей.

13. Уравнение прямой на плоскости, его виды.

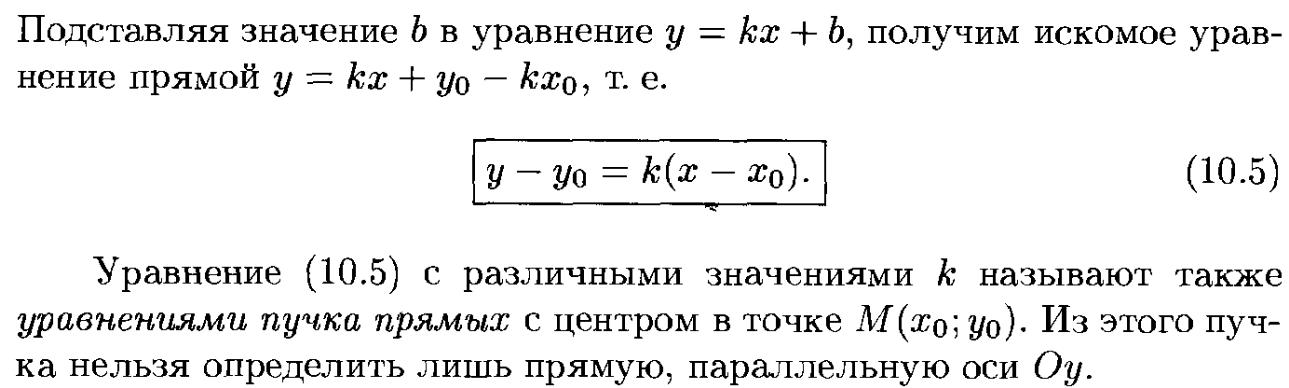
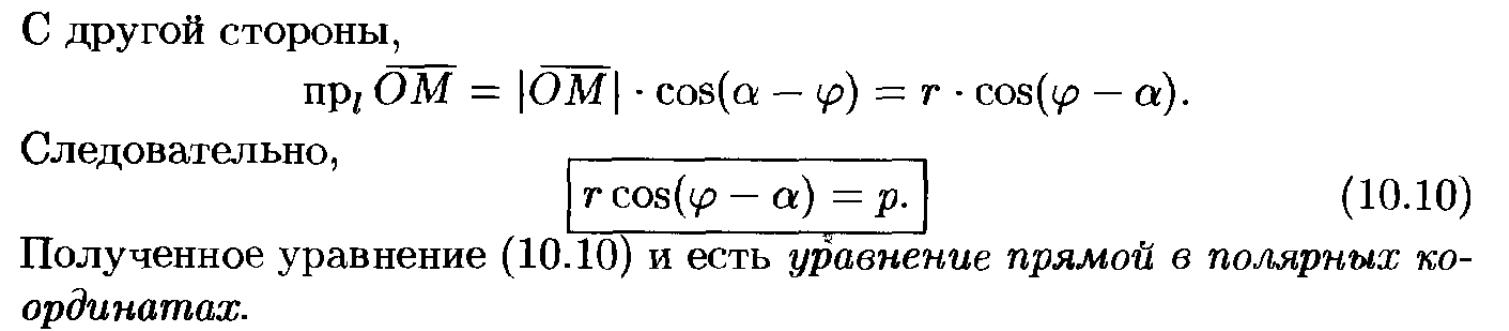
14. Окружность, приведение к каноническому виду, запись полярных координат.

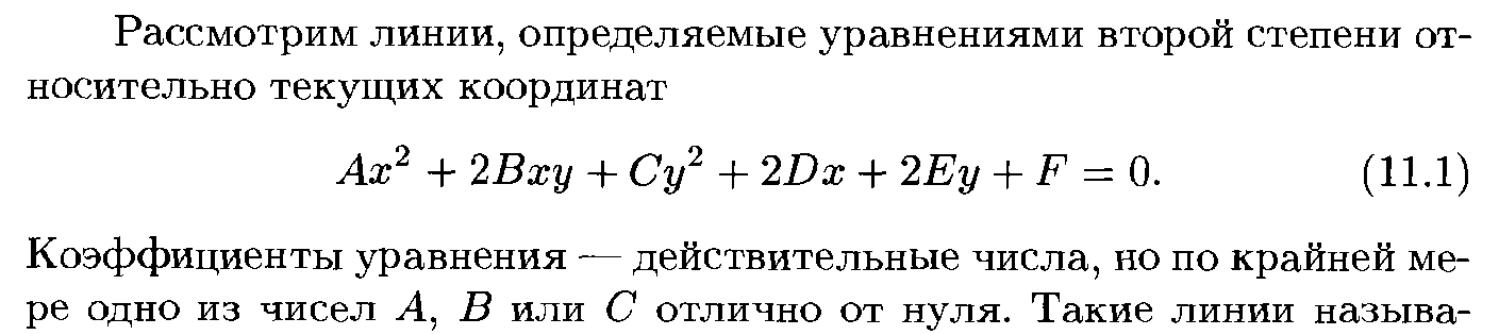
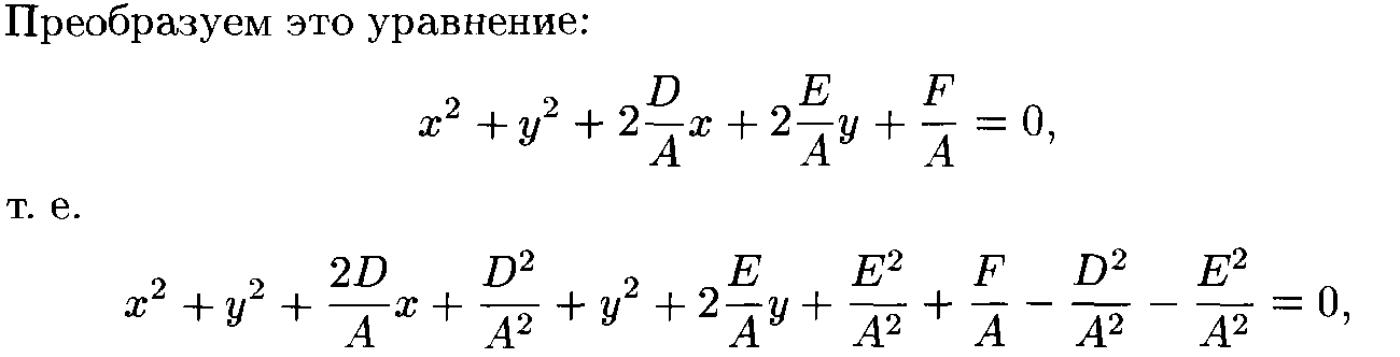
15. Эллипс, его свойства, приведение к каноническому виду.

16. Гипербола, её свойства, приведение к каноническому виду.

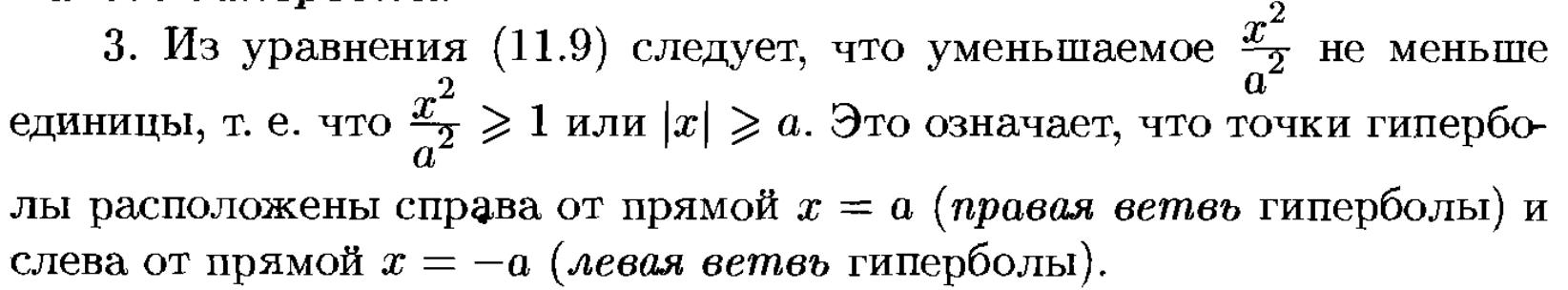
17. Парабола, её свойства, приведение к каноническому виду.

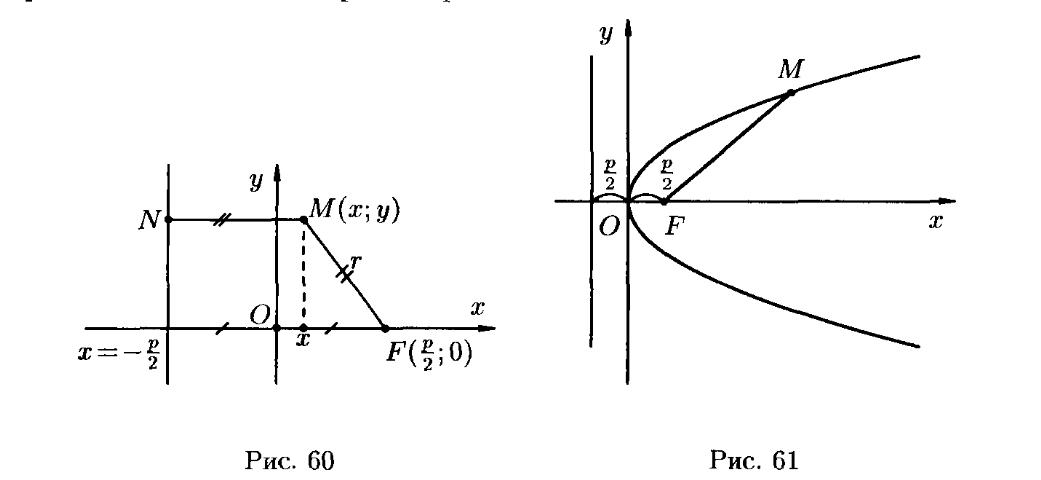
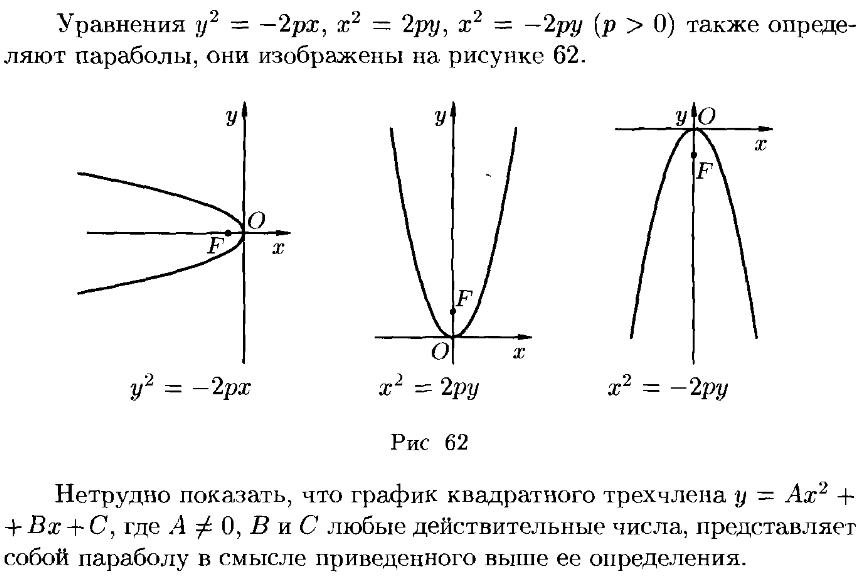
18. Уравнения плоскости.

19. Уравнения прямой в пространстве.

20. Кривые 2-го порядка. Приведение к каконическому виду. Параллельный перенос.

В плоскости, в некоторой прямоугольной системе координат  ,  , пусть задана кривая, определяемая неявно уравнением второй степени

,                                                         (1)

где   - заданные действительные числа. При этом числа   одновременно не равны нулю. Эта кривая называется кривой второго порядка. На самом деле может случиться, что нет вовсе точек   с действительными координатами, удовлетворяющих уравнению (1). В этом случае говорят, что уравнение (1) определяет мнимую кривую второго порядка.

, рассматривается произведение  .

• Если   , то эллипс;

• Если   , то гипербола;

• Если 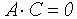  , то парабола.

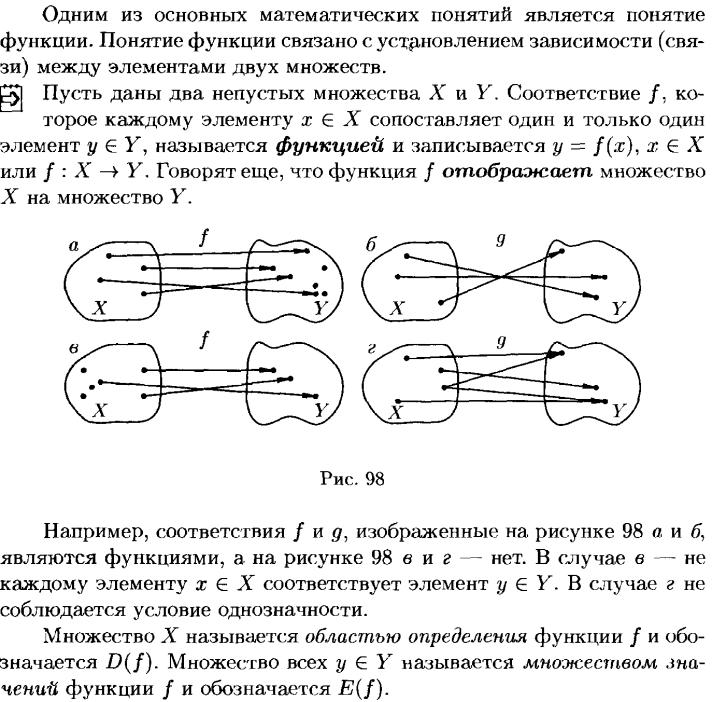
21. Понятие функции. График элементарной функции

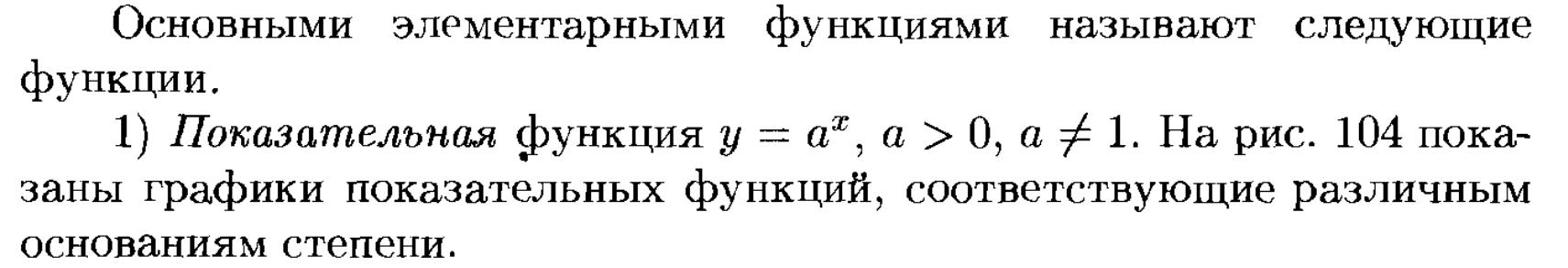
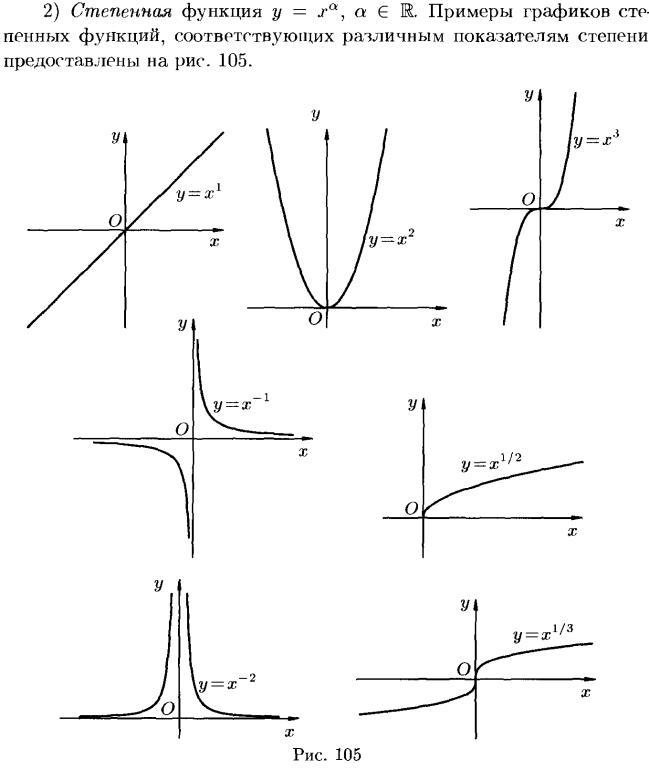
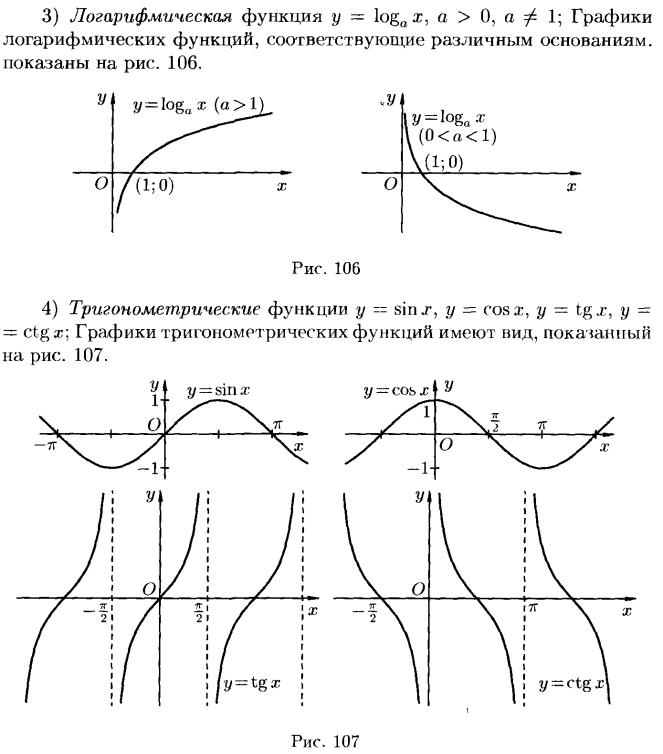
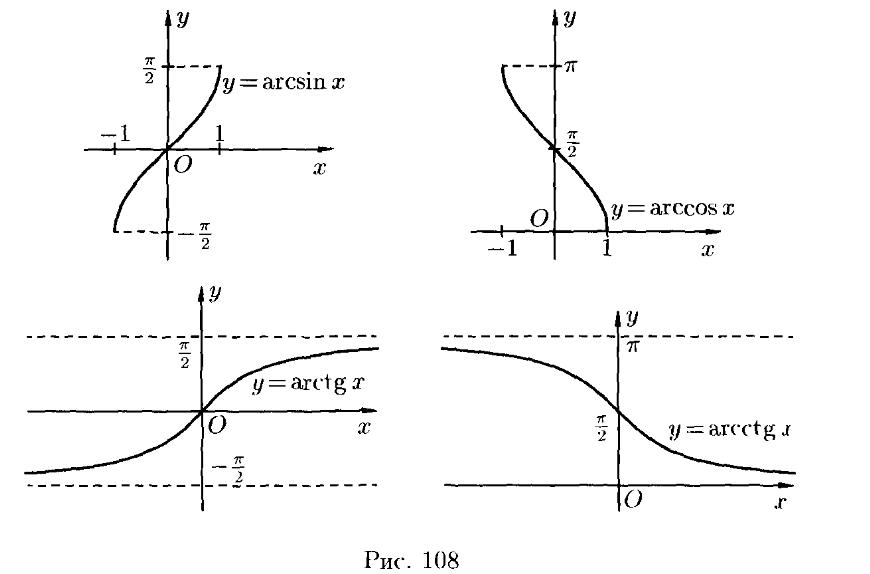
22. Понятие предела числовой последовательности, основные теоремы о пределах.

Под числовой последовательностью х1, х2, х3, …,хn,… понимается функция:

(1)

заданная на множестве N натуральных чисел. Кратко последовательность обозначается в виде {xn} или xn, где n N. Число х1 называется первым членом последовательности, х2 – вторым, …, xn – общим или n-ым членом последовательности.

Чаще всего последовательность задаётся формулой его общего члена. Формула (1) позволяет вычислить любой член последовательности по номеру n.

Последовательность {xn} называется ограниченной, если существует такое число М>0, что для любого n N выполняется неравенство: |xn| ≤ M.

В противном случае последовательность называется неограниченной. Легко видеть, что последовательности yn, un ограничены, а vn, zn - неограниченны.

Последовательность {xn} называется возрастающей (неубывающей), если для любого n выполняется неравенство: an+1 > an (an+1 ≥ an). Аналогично определяется убывающая (невозрастающая) последовательность. Все эти последовательности называются монотонными.

Если все элементы последовательности равны одному и тому же числу, то её называют постоянной.

Число a называется пределом последовательности {xn}, если для любого положительного числа ε найдётся такое натуральное число N, что при всех n > N выполняется неравенство: |xn – a| < ε.

В этом случае пишут:

, и говорят, что последовательность {xn} имеет предел равный числу a. Говорят также, что последовательность {xn} сходится к a.

Не всякая последовательность имеет предел. Признак существования предела последовательности.

Теорема Вейерштрасса: Всякая монотонная ограниченная последовательность имеет предел.

На основании этой теоремы последовательность:

имеет предел

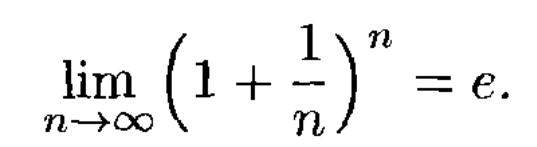
е – неперово число, иррациональное число, приближённое значение равно 2,72, неперово число принято за основание натуральных логарифмов:

ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ.

Представлены теоремы, облегчающие нахождение пределов функций.

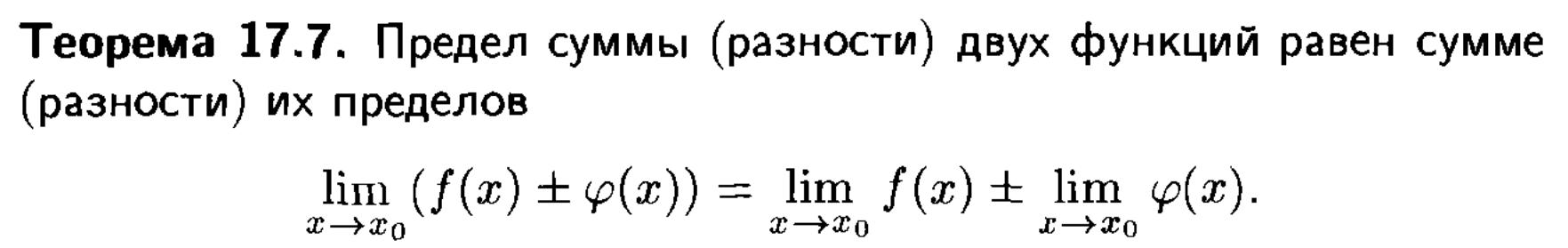
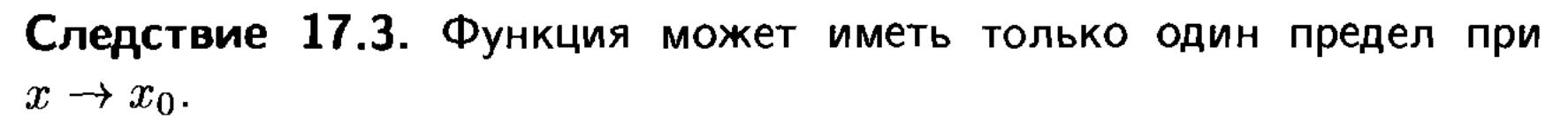
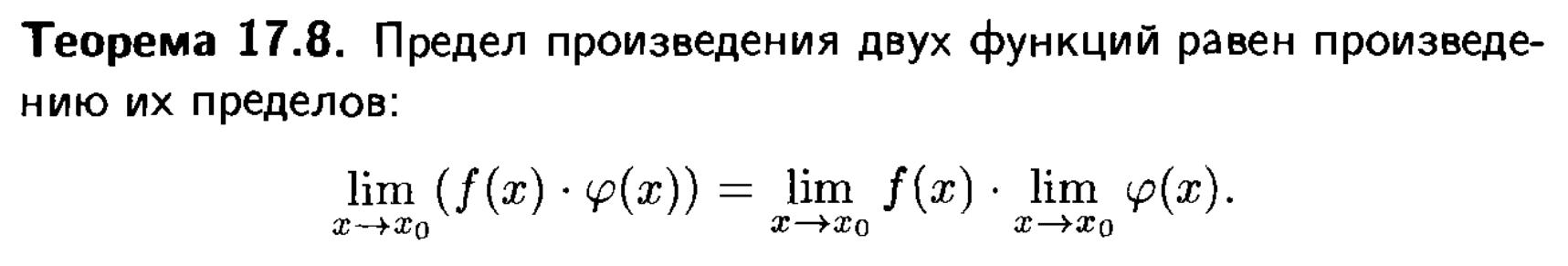
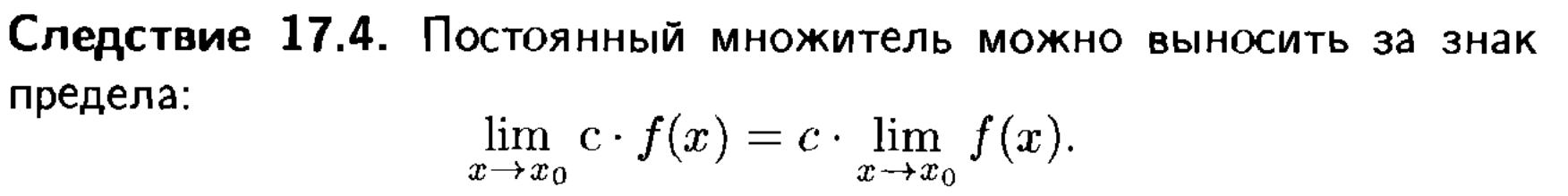
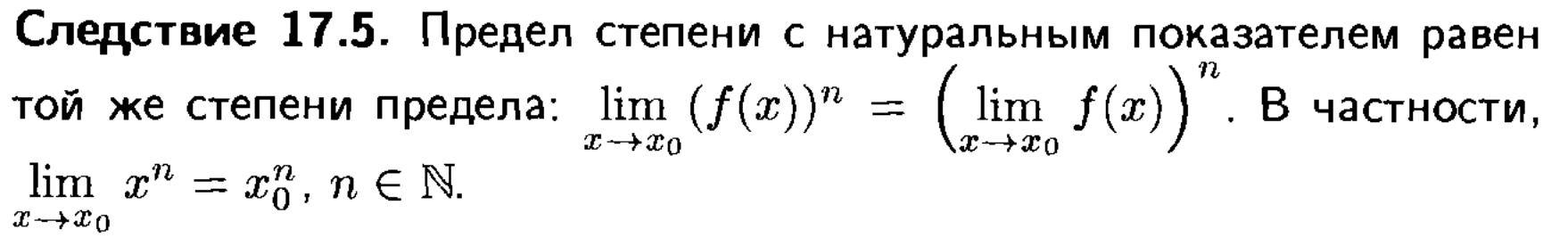
23. Понятие предела функции. Теоремы о пределах.

ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ.

Представлены теоремы, облегчающие нахождение пределов функций.

24. 1Й и 2й замечательные пределы.

ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ.

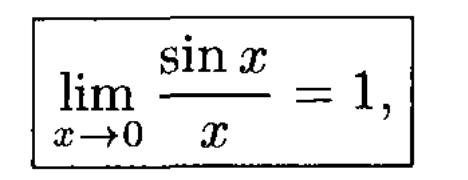
называемый первым замечательным пределом. Читается: предел отношения синуса к его аргументу равен единице, когда аргумент стремится к 0.

ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ.

,

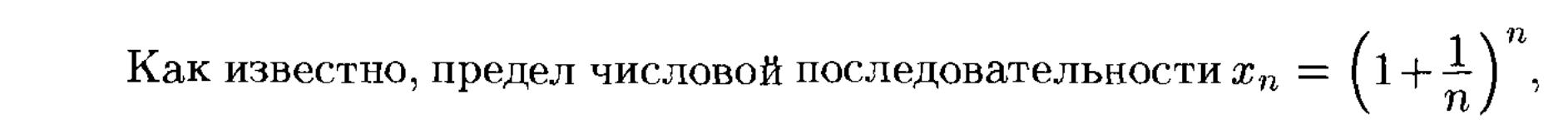
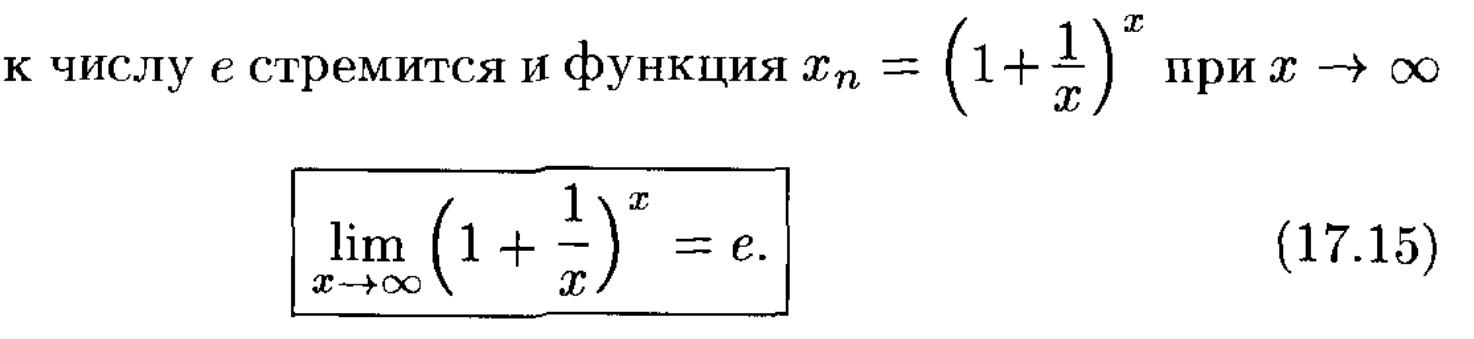
25. Понятие неопределенности и способы ее раскрытия.

При переходе к функциям более сложного вида сталкиваются с появлением выражений, значение которых не определено. Такие выражения называют неопределенностями.

Перечислим все основные виды неопределенностей: ноль делить на ноль   (0 на 0), бесконечность делить на бесконечность  , ноль умножить на бесконечность  , бесконечность минус бесконечность  , единица в степени бесконечность  , ноль в степени ноль  , бесконечность в степени ноль  .

ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.

Раскрывать неопределенности позволяет:

1. упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);

2. использование замечательных пределов;

3. применение правила Лопиталя;

Правило Лопиталя очень широко применяется для вычисления пределов, когда имеет место неопределенность вида ноль делить на ноль  , бесконечность делить на бесконечность  .

К этим видам неопределенностей сводятся неопределенности ноль умножить на бесконечность   и бесконечность минус бесконечновть  .

Дифференцирование функции и нахождение производной является неотъемлемой частьюправила Лопиталя, так что рекомендуем обращаться к этому разделу.

Формулировка правила Лопиталя cледующая:

Если 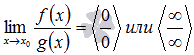 , и если функции f(x) и g(x) – дифференцируемы в окрестности точки  , то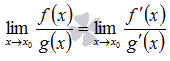 

В случае, когда неопределенность не исчезает после применения правила Лопиталя, то его можно применять вновь.

4. использование замены бесконечно малого выражения ему эквивалентным (использование таблицы эквивалентных бесконечно малых).

ВАЖНЕЙШИЕ ЭКВИВАЛЕНТНОСТИ, ИСПОЛЬЗУЕМЫЕ ПРИ ВЫЧИСЛЕНИИ ПРЕДЕЛОВ.

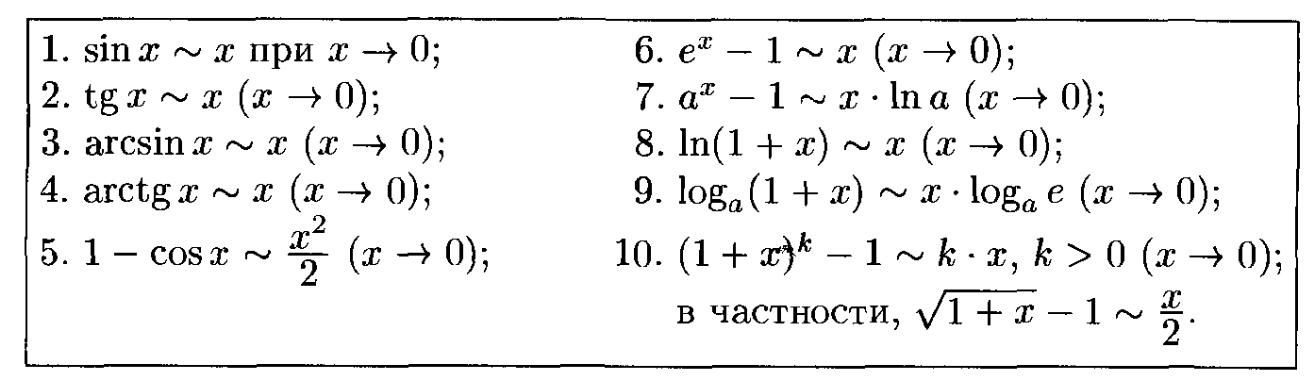
Сгруппируем неопределенности в таблицу неопределенностей. Каждому виду неопределенности поставим в соответствие метод ее раскрытия (метод нахождения предела).

Эта таблица вместе с таблицей пределов основных элементарных функций будут Вашими главными инструментами при нахождении любых пределов.