6. Определение отношения напряженности отраженного от ионосферы сигнала к напряженности поверхностного сигнала.
Зависимость
максимальных ошибок слежения за фазой
и огибающей
,
обусловленных влиянием ионосферного
сигнала выражаются следующими
формулами:
Здесь tЗ – задержка пространственных сигналов по отношению к поверхностным (рис. 2.19. Задержка пространственных радиоволн по отношению к поверхностным для колебаний на частоте 100 кГц, учебника [1]).
Ошибка измерения фазы и огибающей появляется при задержке отраженного сигнала относительно поверхностного меньше, чем tЗ , то есть tЗ < t0. Судя по графику (рис. 2.19. учебника [1].) в нашем случае ошибка имеет место быть при уровне слежения 0,5 начиная с дистанции 600 миль, т.к. в остальных случаях не выполняется выше сказанное условие.
Уровень слежения 0.5: t0 = 45.7 мкс;
Дальность R, миль |
EПОВ (PИЗЛ = 1600 кВт), мкВ/м |
EПР (PИЗЛ = 1600 кВт), мкВ/м |
TЗАД , мкс |
ЕПР /ЕПОВ |
|
|
|
В разах |
В дБ |
||||||
600 |
565,02 |
2831,78 |
45,7 |
5,01 |
14,0 |
0 |
0 |
700 |
633,96 |
1786,73 |
42,0 |
2,82 |
9,0 |
0,18 |
0,07 |
800 |
598,49 |
1127,35 |
41,0 |
1,88 |
5,5 |
0,38 |
0,11 |
900 |
565,02 |
711,31 |
40,0 |
1,26 |
2,0 |
0,63 |
0,14 |
1000 |
448,81 |
448,81 |
39,0 |
1,00 |
0,0 |
1,06 |
0,20 |
1100 |
400,00 |
283,18 |
38,7 |
0,71 |
-3,0 |
0,92 |
0,16 |
1200 |
283,18 |
178,67 |
38,5 |
0,63 |
-4,0 |
0,93 |
0,16 |
1300 |
200,47 |
112,74 |
38,2 |
0,56 |
-5,0 |
0,99 |
0,16 |
1400 |
141,93 |
79,81 |
38,1 |
0,56 |
-5,0 |
1,05 |
0,17 |
1500 |
94,85 |
56,50 |
38,1 |
0,60 |
-4,5 |
1,13 |
0,18 |
1600 |
63,40 |
40,00 |
38,1 |
0,63 |
-4,0 |
1,18 |
0,19 |
1700 |
40,00 |
25,24 |
38,1 |
0,63 |
-4,0 |
1,18 |
0,19 |
1800 |
26,73 |
17,87 |
38,1 |
0,67 |
-3,5 |
1,26 |
0,20 |
1900 |
17,87 |
11,27 |
38,1 |
0,63 |
-4,0 |
1,18 |
0,19 |
2000 |
11,27 |
7,11 |
38,1 |
0,63 |
-4,0 |
1,18 |
0,19 |
2100 |
7,11 |
4,00 |
38,1 |
0,56 |
-5,0 |
1,05 |
0,17 |
,
рад·10 -3
,
мкс7. Вычисление суммарных ошибок отсчетов по фазе и огибающей to для двух уровней слежения.
Суммарные ошибки отсчетов по фазе и огибающей to определяются выражениями:
,
инс = 0,05
– относительная инструментальная
ошибка изменения фазы (относительно
фазового цикла); tинс = 0,5
мкс – инструментальная ошибка изменения
по огибающей.
для
уровня 0,3.
Сведем исходные данные для расчета в таблицу.
R, миль |
, рад·10 -3 |
, мкс |
, рад·10 -3 |
, мкс |
||
0,3 |
0,5 |
0,3 |
0,5 |
|||
0 |
0,01 |
0,01 |
0,0002 |
0,0002 |
0 |
0 |
100 |
0,03 |
0,02 |
0,0007 |
0,0005 |
0 |
0 |
200 |
0,08 |
0,05 |
0,0018 |
0,0013 |
0 |
0 |
300 |
0,17 |
0,10 |
0,0041 |
0,0028 |
0 |
0 |
400 |
0,38 |
0,23 |
0,0091 |
0,0063 |
0 |
0 |
500 |
0,77 |
0,46 |
0,0182 |
0,0126 |
0 |
0 |
600 |
1,36 |
0,82 |
0,0323 |
0,0225 |
0 |
0 |
700 |
2,16 |
1,30 |
0,0512 |
0,0356 |
0,18 |
0,07 |
800 |
3,42 |
2,05 |
0,0812 |
0,0565 |
0,38 |
0,11 |
900 |
5,42 |
3,25 |
0,1287 |
0,0896 |
0,63 |
0,14 |
1000 |
8,59 |
5,15 |
0,2038 |
0,1418 |
1,06 |
0,20 |
1100 |
13,63 |
8,18 |
0,3236 |
0,2251 |
0,92 |
0,16 |
1200 |
21,57 |
12,94 |
0,5120 |
0,3561 |
0,93 |
0,16 |
1300 |
34,29 |
20,57 |
0,8138 |
0,5661 |
0,99 |
0,16 |
1400 |
48,37 |
29,02 |
1,1479 |
0,7985 |
1,05 |
0,17 |
1500 |
68,58 |
41,15 |
1,6276 |
1,1322 |
1,13 |
0,18 |
1600 |
95,72 |
57,43 |
2,2718 |
1,5804 |
1,18 |
0,19 |
1700 |
153,16 |
91,89 |
3,6349 |
2,5286 |
1,18 |
0,19 |
1800 |
218,79 |
131,28 |
5,1927 |
3,6122 |
1,26 |
0,20 |
1900 |
353,44 |
212,06 |
8,3882 |
5,8352 |
1,18 |
0,19 |
2000 |
574,34 |
344,60 |
13,6309 |
9,4822 |
1,18 |
0,19 |
2100 |
918,94 |
551,36 |
21,8094 |
15,1714 |
1,05 |
0,17 |
Результаты расчетов также сведем в таблицу.
R, миль |
|
|
||
0,3 |
0,5 |
0,3 |
0,5 |
|
0 |
0,0500 |
0,0500 |
0,5000 |
0,5000 |
100 |
0,0500 |
0,0500 |
0,5000 |
0,5000 |
200 |
0,0500 |
0,0500 |
0,5000 |
0,5000 |
300 |
0,0500 |
0,0500 |
0,5000 |
0,5000 |
400 |
0,0500 |
0,0500 |
0,5001 |
0,5000 |
500 |
0,0500 |
0,0500 |
0,5003 |
0,5002 |
600 |
0,0500 |
0,0500 |
0,5010 |
0,5005 |
700 |
0,0500 |
0,0500 |
0,5075 |
0,5061 |
800 |
0,0501 |
0,0500 |
0,5184 |
0,5151 |
900 |
0,0503 |
0,0501 |
0,5349 |
0,5269 |
1000 |
0,0507 |
0,0503 |
0,5758 |
0,5569 |
1100 |
0,0518 |
0,0507 |
0,6167 |
0,5712 |
1200 |
0,0545 |
0,0517 |
0,7333 |
0,6344 |
1300 |
0,0606 |
0,0541 |
0,9684 |
0,7721 |
1400 |
0,0696 |
0,0578 |
1,2636 |
0,9573 |
1500 |
0,0849 |
0,0648 |
1,7122 |
1,2507 |
1600 |
0,1080 |
0,0762 |
2,3339 |
1,6685 |
1700 |
0,1611 |
0,1046 |
3,6740 |
2,5846 |
1800 |
0,2244 |
0,1405 |
5,2205 |
3,6521 |
1900 |
0,3570 |
0,2179 |
8,4052 |
5,8597 |
2000 |
0,5765 |
0,3482 |
13,6414 |
9,4973 |
2100 |
0,9203 |
0,5536 |
21,8158 |
15,1806 |
,
рад
,
мкс
Рис. 9. График суммарных ошибки отсчетов по фазе для двух уровней слежения.
Рис. 10. График суммарных ошибок отсчетов по огибающей to для двух уровней слежения.
Определим
надежность устранения многозначности
фазовых измерений P = f(R)
по формуле:
,
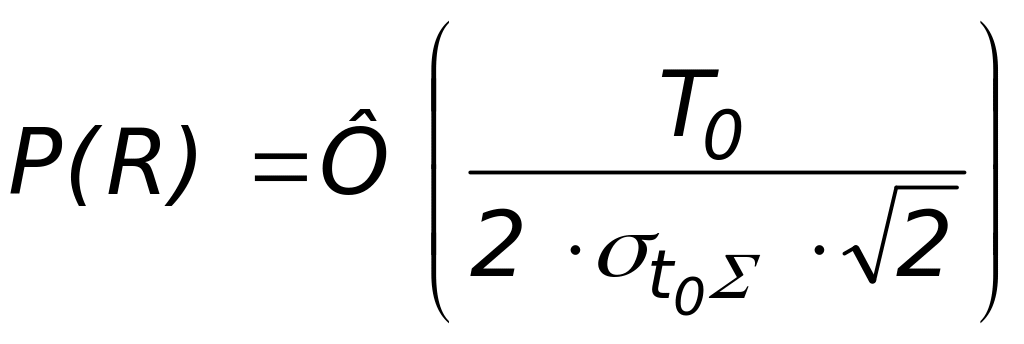где: T0 = 10 мкс
– период высокочастотного заполнения.
R, миль |
, мкс |
P(R) |
||
0,3 |
0,5 |
0,3 |
0,5 |
|
0 |
0,5000 |
0,5000 |
1,000 |
1,000 |
100 |
0,5000 |
0,5000 |
1,000 |
1,000 |
200 |
0,5000 |
0,5000 |
1,000 |
1,000 |
300 |
0,5000 |
0,5000 |
1,000 |
1,000 |
400 |
0,5001 |
0,5000 |
1,000 |
1,000 |
500 |
0,5003 |
0,5002 |
1,000 |
1,000 |
600 |
0,5010 |
0,5005 |
1,000 |
1,000 |
700 |
0,5075 |
0,5061 |
1,000 |
1,000 |
800 |
0,5184 |
0,5151 |
1,000 |
1,000 |
900 |
0,5349 |
0,5269 |
1,000 |
1,000 |
1000 |
0,5758 |
0,5569 |
1,000 |
1,000 |
1100 |
0,6167 |
0,5712 |
1,000 |
1,000 |
1200 |
0,7333 |
0,6344 |
1,000 |
1,000 |
1300 |
0,9684 |
0,7721 |
1,000 |
1,000 |
1400 |
1,2636 |
0,9573 |
1,000 |
1,000 |
1500 |
1,7122 |
1,2507 |
0,997 |
1,000 |
1600 |
2,3339 |
1,6685 |
0,968 |
0,997 |
1700 |
3,6740 |
2,5846 |
0,826 |
0,947 |
1800 |
5,2205 |
3,6521 |
0,662 |
0,829 |
1900 |
8,4052 |
5,8597 |
0,448 |
0,606 |
2000 |
13,6414 |
9,4973 |
0,286 |
0,401 |
2100 |
21,8158 |
15,1806 |
0,181 |
0,258 |
Рис. 11. Графики зависимости вероятности устранения вероятности от дальности.