Контрольные вопросы

1. Что такое скаляр, вектор, матрица? Дайте определения и примеры.

2. Какие действия можно проводить с векторами и матрицами? Привести примеры.

3. Как в MATLABе формируются массивы: одномерные и двумерные? Дать примеры.

4. Дайте определение транспонированному вектору и транспонированной матрице. Как они формируются в MATLABе? Привести примеры.

5. Дайте определение детерминанту и обратной матрице. Как они вычисляются в MATLABе? Привести примеры.

6. Элементарные функции и их запись в MATLABе. Привести примеры.

7. Выполнить вручную (без помощи компьютера) следующие действия:

- умножить вектор P на вектор Y;

- умножить матрицу G на вектор Y;

- умножить матрицу G на матрицу F,

где:

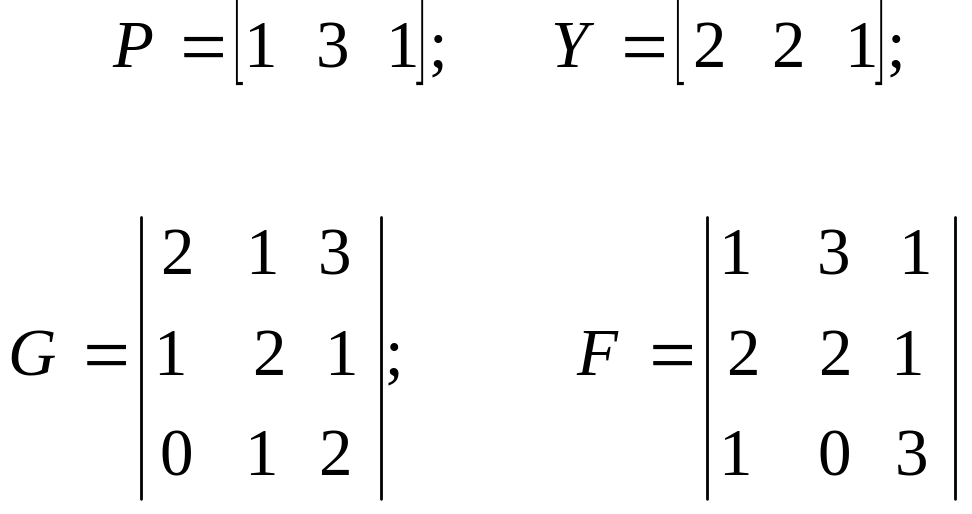
8. Написать программу на MATLABе для выполнения действий, указанных в вопросе 7.

9. Дана матрица . Определить без помощи компьютера обратную ей матрицу – A^-1.

10. Найти без помощи компьютера детерминант матрицы .

11. Дана система линейных уравнений: (1P)

или в матричном виде CּX = B.

Составить на MATLABе программу решения этой системы с определением детерминанта матрицы С.

12. Найти с помощью MATLABа матрицу, обратную матрице С (из вопроса 11). Как с помощью матрицы С^-1 найти неизвестные x₁, x₂, x₃, x₄ из системы (1P)?

13. Решить с помощью MATLABа систему уравнений (2P)

Найти причину неудачи, если система (2P) не решается. Определить детерминант матрицы коэффициентов при неизвестных.

14.Для условий вопроса 7 написать на MATLABе программу:

- умножения 1-ой строки матрицы G на 2-ой столбец матрицы F;

- умножения 2-ой строки матрицы F на 2-ой столбец матрицы G.

15. С помощью MATLABа для зависимости длины тормозного пути S (м) в функции от скорости V_f (м/с):

,

где скорость задана в интервале V_f = 10…40 (шаг по скорости равен 2м/с), построить графики зависимостей: S = f(V_f) и V_f = φ(S).

16. Решить графически (с помощью MATLABа) уравнение:

(3P)

в интервале x = 0…10π с шагом 0,1π. Сколько корней имеет уравнение (3P)?

17. С помощью MATLABа в декартовых координатах построить окружность с центром в точке x = 1, y = 1 и радиусом, равным 1. По оси x выбрать шаг Δx = 0,05.

18. С помощью MATLABа построить зависимость y = ln(x + 1) в декартовых координатах в интервале x = 0…4π с шагом 0,2π, а также зависимость r = ln(φ + 1) в полярных координатах в том же интервале и с тем же шагом по φ.

19. С помощью MATLABа на одном графике в полярных координатах с шагом = 0,1 в интервале построить зависимости (спирали с 3-мя оборотами):

а) r = 0,4φ + 0,03φ² (4P)

b) зависимость (4Р), но закрученную в обратном направлении.

20. С помощью MATLABа построить 3-х мерную поверхность:

в области [x, y] = [-1:0,1:1] [-2:0,1:2].

21. С помощью MATLABа построить 3-х мерную поверхность:

в области [x, y] = [0:0,2π:4π] [0:0,2:4].

22. С помощью MATLABа используя программу fzero решить нелинейное уравнение:

с начальным приближением x₀ = 0.

23. С помощью MATLABа используя программу fzero решить нелинейное уравнение:

с начальным приближением x₀ = 4.

24. С помощью MATLABа используя программу fminsearch решить систему нелинейных уравнений:

25. С помощью MATLABа используя программу quad найти приближенное значение интеграла:

Построить график подинтегральной функции с шагом 0,2 в интервале интегрирования.

26. С помощью MATLABа используя программу quad вычислить площадь полигона для испытания автомобилей (Фиг. 1P)

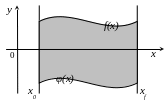
Фигура 1P. Схема испытательного полигона, где:

x₀ = 2км; x_f = 8км.

27. Дана табличная зависимость потребления горючего (для легкового автомобиля) от времени эксплуатации.

t (год)	1	2	3	5	8	12
G (л/час)	6,1	6,4	7,1	7,4	8,1	8,6

С помощью пакета MATLAB (функции polyfit, polyval) найти аппроксимирующую зависимость G = f(t) полиномом 3-ей степени и определить среднюю ошибку аппроксимации.

28. Дана табличная зависимость стоимости легкового автомобиля от времени эксплуатации.

t (год)	0	1	2	3	5	7	10
C ($)	11500	8700	7200	6000	5500	5000	4600

С помощью пакета MATLAB (функции polyfit, polyval) найти аппроксимирующие зависимости C = f(t) полиномами 2-ой и 3-ейстепени и сравнить максимальные ошибки аппроксимации.

29. С помощью MATLABа (функция ode45) решить обыкновенное дифференциальное уравнение:

(5P)

в интервале x = 0…2 при начальных условиях: x₀ = 0, y₀ = 1. Предварительно уравнение (5P) преобразовать в систему 2-х дифференциальных уравнений.

30. С помощью MATLABа (функция ode23) решить обыкновенное дифференциальное уравнение:

(6P)

в интервале x = 0…5 при начальных условиях: x₀ = 0, y₀ = 2. Предварительно уравнение (6P) преобразовать в систему 2-х дифференциальных уравнений.

31. С помощью MATLABа (функция ode45) решить систему обыкновенных дифференциальных уравнений:

в интервале t = 0…8π при начальных условиях: t =0; x₀ = 1; y₀ = 1.

32. С помощью MATLABа (функция ode45) решить систему обыкновенных дифференциальных уравнений:

в интервале  = 0,3…4 при начальных условиях:  = 0,3; x₀ = 1; y₀ = 0.

33. С помощью MATLABа (функция ode23) решить обыкновенное дифференциальное уравнение:

(7P)

в интервале t = 0…3c при начальных условиях: t = 0, r₀ = 0, и ω = 2π (рад/с). Предварительно уравнение (7P) преобразовать в систему дифференциальных уравнений первого порядка.