Таким образом, задача включает целевую функцию (3.41), ограничения (3.42) и ограничения

x_i ≥ 0 и целые, i =1,…,6.

P4. Транспортная задача. Объединение “Алдермыш-F” имеет 3 фабрики (AF1, AF2, AF3) по производству молочной продукции, которую необходимо развозить каждый день по 4-м населенным пунктам: К1, К2, К3, К4. Фабрики производят в сутки: AF1 – 3 тонны, AF2 – 5 тонн, AF3 – 4 тонны. Населенным пунктам требуется в сутки молочной продукции в количестве: К1 – 2 тонны, К2 – 4 тонны, К3 – 1 тонна, К4 – 5 тонн. Транспортные расходы на 1 кг продукции приведены в Таблице 3.2:

Таблица 3.2 Транспортные расходы (C_ij) на доставку продукции (руб/кг)

	К1	К2	К3	К4
AF1	1,1	0,5	1,5	0,3
AF2	0,6	0,5	*	1,5
AF3	1,3	0,2	1,1	0,7

* - нет дороги

Эти расходы требуется минимизировать, т.е. найти оптимальное количество продукции, которое следует отправить с каждой фабрики в каждый населенный пункт. Формулировка задачи:

a) Выбор варьируемых параметров. Примем, что такими параметрами являются:

x_ij – количество продукции, перевозимой с i-ой фабрики в j-ый населенный пункт. Таким образом, общее число варьируемых параметров равно 12 (i = 1,…,3; j = 1,…,4). В связи с отсутствием дороги между фабрикой AF2 и пунктом К3 примем условно транспортные расходы на этом участке очень высокими, например, 20 руб/кг.

b) Определение целевой функции. Общие расходы составляют:

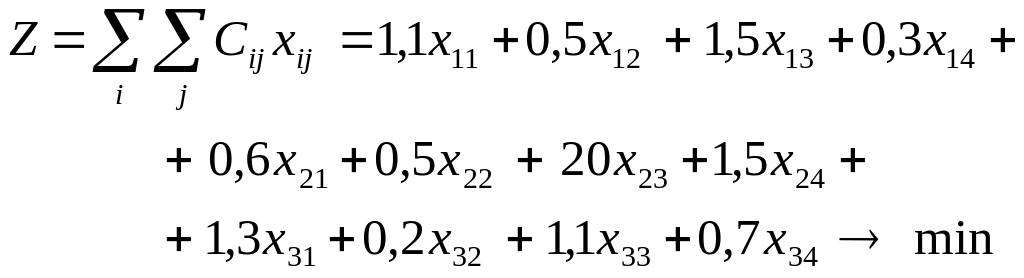(3.43)

Величину Z необходимо минимизировать.

c) Формирование ограничений. Каждая фабрика имеет ограничения по производительности, поэтому можем написать следующие соотношения:

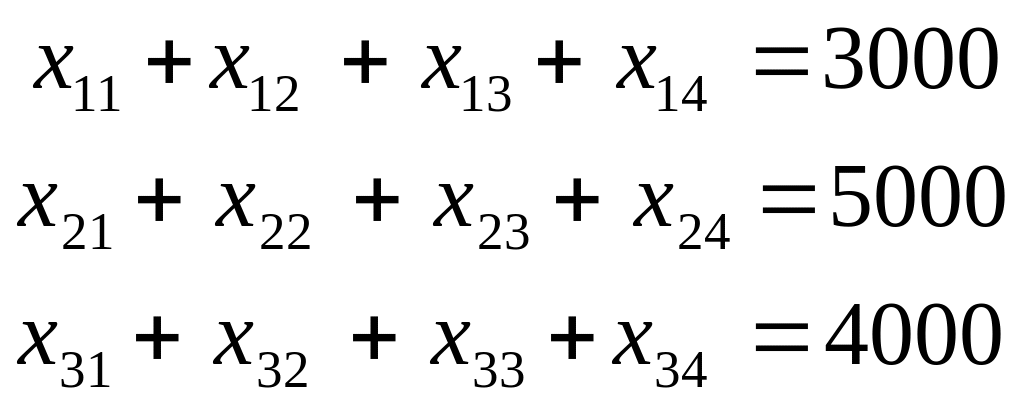(3.44)

Каждый населенный пункт имеет ограничения по потреблению, поэтому можем написать следующие соотношения:

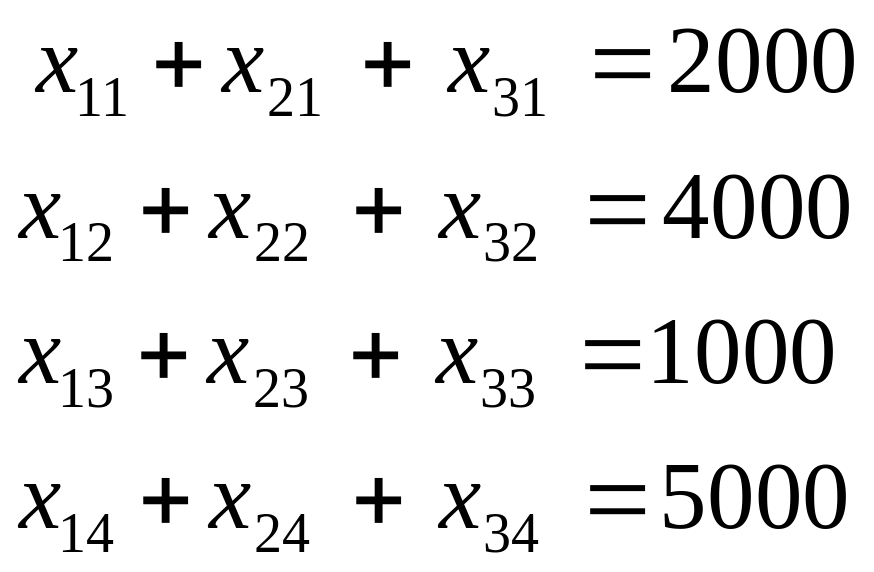(3.45)

Запишем также ограничения по неотрицательности варьируемых параметров: .

Таким образом, данная транспортная задача является задачей линейной оптимизации, имеет 12 варьируемых параметров, 7 ограничений типа “равенство”, 12 ограничений типа “неравенство” и требуется найти Z_min и соответствующие ей значения .

Контрольные вопросы

1. Что такое “ прототип ” математической модели?

2. Какая разница между специалистом предметной области и математиком? Специалистом какой предметной области вы станете после окончания университета?

3. Приведите какие-либо уравнения с граничными и начальными условиями. Какая разница между граничными и начальными условиями?

4. К задаче “Нейтрализатор продуктов сгорания”:

а) приведите пример пористого тела из (вашего опыта). Что такое пористость?

б) выведите формулу для площади каталитического слоя (F).

в) что такое Re, ρ, W, в данной задаче?

г) Напишите формулу для определения давления на выходе из нейтрализатора.

д) Какие величины являются неизвестными в этой задаче?

е) Выведите формулу (3.10).

5. К задаче “Охлаждение помещения”:

а) Что такое Q⁺ и Q^─ ? Зачем эти величины исключаются из математической модели?

б) Объясните физический смысл уравнения (3.15).

в) Запишите полностью итоговую математическую модель с начальными и граничными условиями (без промежуточных соотношений).

г) Какие величины в этой модели являются неизвестными?

д) Что такое ?

6. К задаче “Зарплата и занятость”:

а) Выполните преобразования от уравнений (3.19, 3.20) к уравнению (3.22).

б) Почему в уравнении (3.22) 2 начальных условия? Как получены эти начальные условия?

в) Чем отличаются общее и частное решения дифференциального уравнения?

г) Укажите принципиальный характер изменения решения p(t)?

д) Используя соотношение (3.24) выведите формулу для определения N(t)?

7. Что такое “простые” задачи оптимизации? Приведите примеры.

8. Перечислите свойства задач оптимизации. Что такое функция цели?

9. Какая разница между задачами: линейной оптимизации, нелинейной оптимизации, целочисленной оптимизации?

10. Что такое “Формулировка задач оптимизации”? Каким этапом математического моделирования она соответствует, а каким – нет?

11. В задаче P1 по ряду обстоятельств произошло следующее изменение условий:

а) Цена на мясо увеличилась до 210 руб/кг, хлеба на одного ученика в неделю требуется не менее 1 кг. Переформулируйте задачу по отношению к начальному варианту?

б) Крупу изъяли из рациона и вместо нее ввели макароны стоимостью 15 руб/кг со следующим содержанием полезных веществ: белки – 0,2 кг белков на 1 кг макарон; жиры – 0,1 кг; углеводы – 0,6 кг; витамины – 0,08 кг. Переформулируйте задачу по отношению к начальному варианту.

12. В задаче P2 произошли следующие изменения:

а) увеличилось число специалистов. Предприятие теперь располагает: 1800 часов на создание компонентов, 2400 часов на монтаж и 800 часов на отладку. Кроме того, в связи с покупкой нового оборудования сократилось время на монтаж одной единицы: модели А – до 3 часов, B – до 3,5 часов, С – до 6 часов. Переформулируйте задачу по отношению к начальному варианту.

б) в производство внедрили новую модель радиоприемника типа D, которая обеспечивает прибыль 250 руб. за единицу продукции при затратах времени: 0 часов на изготовление компонента (все компоненты покупные), 3 часа – на монтаж и 1 час на отладку. В течение недели должно быть изготовлено не менее 10 единиц этой модели. Переформулируйте задачу по отношению к начальному варианту.

13. В задаче “Охрана магазина” дирекция решила разделить дежурство на 8 периодов по 3 часа в каждом и каждый охранник должен дежурить по 3 периода последовательно в течение суток. Распределение охранников по периодам приведено в Таблице 3.3. Переформулируйте задачу по отношению к начальному варианту.

Таблица 3.3 Распределение охранников по периодам

Период	1	2	3	4	5	6	7	8
Число охранн.	9	12	24	32	38	32	24	12

14. В транспортной задаче в связи с открытием новой фабрики (AF4) мощностью 4 тонны молочной продукции в день объединение решило продавать свою продукцию в населенный пункт К5 в количестве 4 тонны в день (но не обязательно только с новой фабрики). Транспортные расходы (руб/кг) с фабрики AF4 до населенных пунктов приведены в Таблице 3.4, а транспортные расходы от других фабрик до населенного пункта К5 приведены в Таблице 3.5. Переформулируйте задачу по отношению к начальному варианту.

Таблица 3.4 Транспортные расходы (руб/кг) с фабрики AF4 до населенных пунктов

Насел.пункт	К1	К2	К3	К4	К5
AF4	2	1,2	3,1	0,7	1,5

Таблица 3.5 Транспортные расходы (руб/кг) до населенного пункта К5

Фабрика	AF1	AF2	AF3
К5	3,2	1,3	2,7