Тема 3. Формирование математических моделей
3.1 Примеры моделей инженерных и экономических задач.
На этом этапе необходимо на базе физической (концептуальной) схемы сформировать набор корректных математических соотношений: уравнений, неравенств, формул для величин типа “черный ящик”. Следует также предусмотреть какую-то совокупность начальных и граничных условий, если это необходимо. Этот набор соотношений должен быть взаимосвязанным и ориентированным на определение искомых характеристик объекта или системы. Обычно математические модели формируются специалистами предметной области (инженер, экономист, физик, биолог и т.д.) хотя математики тоже могут принимать участие. Следует использовать “прототипы”, т.е. уже кем-то сформированные математические модели. При математических преобразованиях необходимо быть внимательным в отношении единиц измерения. Ниже приводятся примеры формирования математических моделей для задач А, B, C, изложенных в Теме 2.
A. Нейтрализатор продуктов сгорания.
Здесь необходимо сформировать математическую модель на основе соотношений:
- уравнения химической кинетики:
(3.1)
где
;
- мольная концентрация
NO в продуктах сгорания.
формула для определения перепада давления (см. Рис. 3.1):
(3.2)
где
= Па; []
- коэффициент гидравлического сопротивления
(безразмерная величина);
[dp]
= м – условный диаметр пор; []
= м2/сек
– кинематическая вязкость; []
– пористость каталитического слоя.
Рисунок 3.1 Фрагмент слоя катализатора
- уравнение расхода:
(3.3)
где
[G] = кг/сек; [F] = м2
- площадь каталитического слоя, через
который проходят продукты сгорания;
;
d, L
– диаметр канала и длина каталитического
слоя.
- уравнение состояния:
(3.4)
где [] = кг/кмоль – молекулярная масса продуктов сгорания.
формула связи мольных долей NO с концентрациями:
(3.5)
Заданными
параметрами являются:
.
Необходимо определить мольную долю NO
на выходе из нейтрализатора (
)
и
.
Этот начальный вариант математической модели, включающий уравнения (3.1 – 3.5) и вспомогательные соотношения, можно упростить. В частности преобразуем формулу (3.2), подставляя в нее вспомогательные соотношения:
(3.6)
Далее, подставив вместо CNO в (3.1) формулу (3.5), получим:
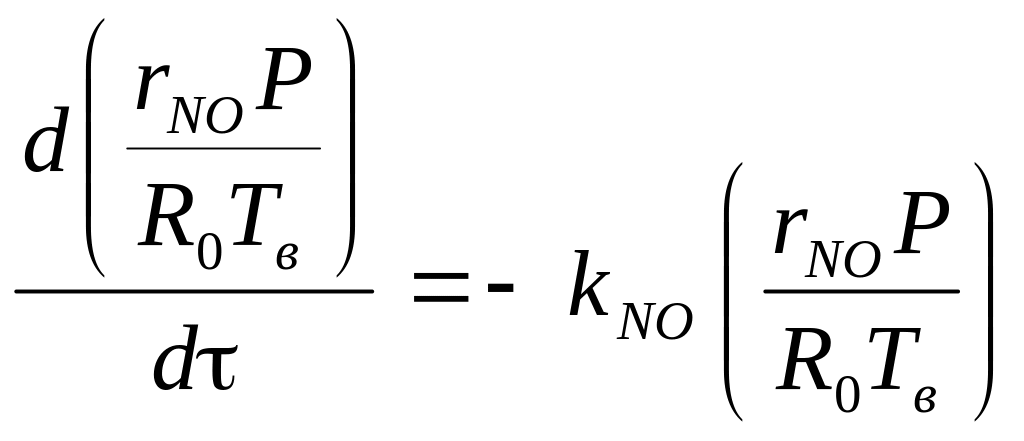(3.7)
Так
как величины
являются постоянными, то их можно вынести
за знак дифференциала и сократить. Тогда
получим:
(3.8)
Считая
kNO
постоянной, можно проинтегрировать
уравнение (3.8):
.
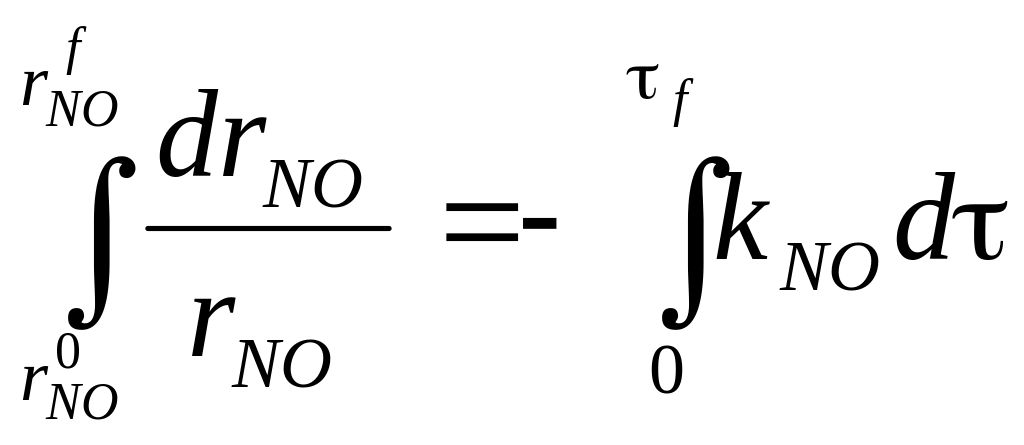Отсюда:
(3.9)
Время движения продуктов сгорания внутри каталитического слоя (f) определяем по формуле:
(3.10)
Тогда окончательно для определения получим простую формулу:
(3.11)
Таким
образом, вся математическая модель
стала простой, выраженной в явном виде
с ясным алгоритмом типа “последовательность
формул”, включающим соотношения (3.6,
3.10, 3.11). Отметим, что в этой модели
используются 2 размерности универсальной
газовой постоянной:
в (3.11) и
в (3.10).
B. Охлаждение помещения мастерской.
При формировании математической модели этой задачи примем, что оборудование имеет массу Mоб и среднюю удельную теплоемкость Cоб. Тогда для внутренней энергии помещения можно записать:
(3.12)
Отсюда, используя (2.5), получим:
(3.13)
Оставляя в левой части (3.13) только производную, получим 1-ое уравнение математической модели:
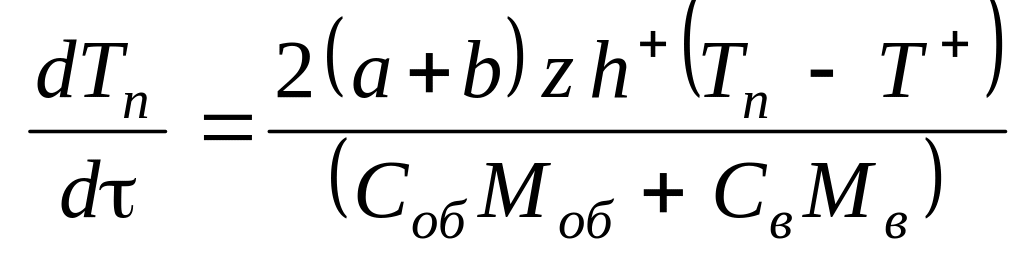(3.14)
Используя
соотношения
и
,
можно исключить
и
(см. 2.6) и тогда в математической модели
появятся еще 2 уравнения:
(3.15)
Последним уравнением математической модели будет уравнение (2.7), которое запишем в виде:
(3.16)
Для этого уравнения необходимо задать начальные и граничные условия:
-
для внутренней поверхности стенки
;
-
начальное распределение температуры
внутри стенки
при x=0,
например, линейное распределение:
(3.17)
Параметрами
модели будут следующие величины:
,
а найти требуется
.
Однако для этого необходимо решить
систему 2-х обыкновенных дифференциальных
уравнений и одного уравнения в частных
производных (3.16) с начальными условиями
(3.17). Аналитически такую систему решить
невозможно, поэтому следует применять
какой-либо из численных методов с
созданием соответствующей программы
расчета.