Задача 9

На заданной сети сформировать поток максимальной мощности, направленный от истока I в сток S, при условии, что пропускные способности ребер сети в обоих направлениях одинаковы. Выписать рёбра, образующие на сети разрез минимальной пропускной способности.

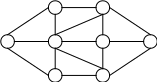10

2 5

19 12 40

15 21

35 17 16

I 1 3 6 8 S

15 24

25 18 29

4 7

19

Решение

10 / 10

2 5

19 / 10 + 9 12 / 9 + 3 40 / 10 + 9 + 3 + 8 + 1

15 / 9 21 / 8 + 1

35 / 16 + 3 + 4 + 8 + 1 17 / 16 + 1 16 / 16

I 1 3 6 8 S

15 / 6 24 / 8

25 / 19 + 6 18 / 6 + 4 + 8 29 / 19 + 6 + 4

4 7

А / В 19 / 19

Выпишем полные пути от истока I к стоку S.

L₁: 1 – 2 – 5 – 8 : 10 ед.

L₂: 1 – 3 – 6 – 8 : 16 ед.

L₃: 1 – 4 – 7 – 8 : 19 ед.

L₄: 1 – 2 – 3 – 5 – 8 : 9 ед.

L₅: 1 – 4 – 3 – 7 – 8 : 6 ед.

L₆: 1 – 3 – 5 – 8 : 3 ед.

L₇: 1 – 3 – 7 – 8 : 4 ед.

L₈: 1 – 3 – 7 – 6 – 5 – 8 : 8 ед.

L₉: 1 – 3 – 6 – 5 – 8 : 1 ед.

Решим задачу табличным методом.

Построим матрицу пропускной способности R.

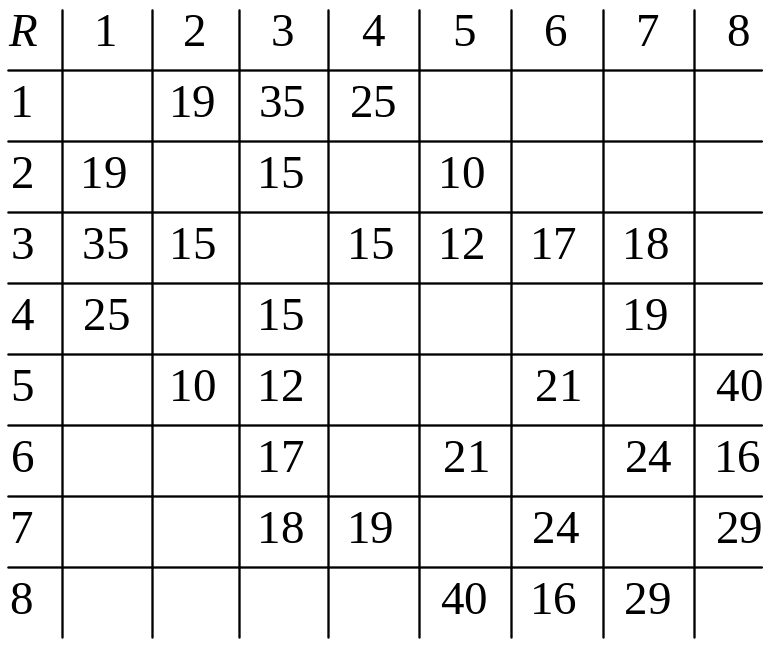
Строим матрицу .

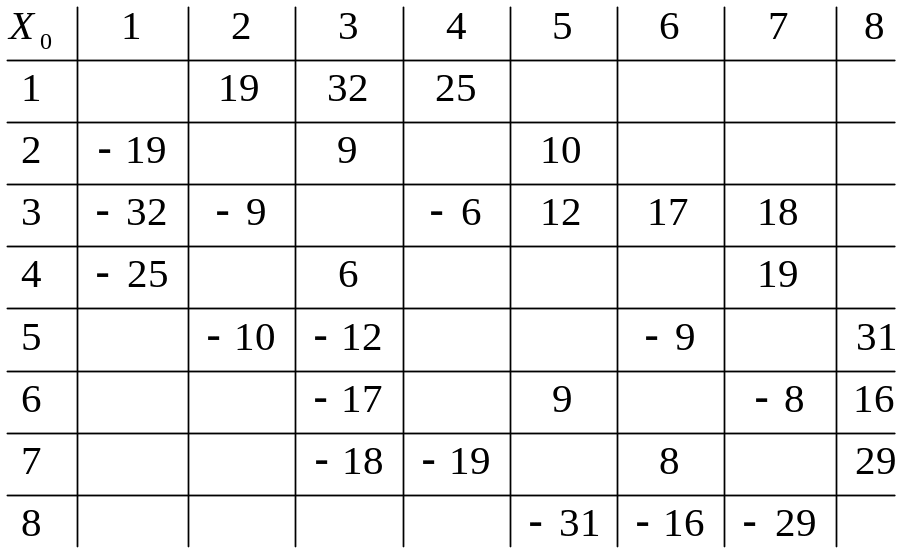
Тогда

Строим множество А – множество вершин, достижимых из истока I по ненасыщенным ребрам.

I // 3

3 // 2, 4

2 // .

4 // .

.

Значит, разрез минимальной пропускной способности:

.

.

.

, значит, по теореме Форда-Фалкерсона данный поток является потоком максимальной мощности.

.