Ортогональное разложение векторов

Определение. Говорят, что вектор ортогонален к подпро­странству , если вектор ортогонален любому вектору из этого подпространства.

Определение. Ортогональным дополнением к подпространству из евклидова пространства называется множество всех век­торов из , ортогональных подпространству . Обозначается .

Определение. Пусть вектор представлен в виде , где , а , тогда вектор называется ортогональной проекцией вектора на подпространство , вектор называется ортогональной составляющей вектора относительно подпространства ,

число называется расстоянием от вектора до подпространства

72

, а угол между векторами и называется углом между вектором и подпространством .

Утверждение. Ортогональное дополнение к подпространству из евклидова пространства само является подпространством евклидова пространства .

Утверждение. Сумма подпространств + является прямой суммой.

Утверждение. Если – некоторое подпространство евклидова пространства , то справедливо равенство + = .

Примеры

1. Найти ортогональную проекцию вектора на подпространство , порождённое векторами

.

Решение. Вначале определим базис данного подпространства. Проверим, являются ли линейно независимыми векторы . Условие линейной независимости (зависимости) данных векторов представляет собой систему уравнений относительно коэффициентов . Найдём решение этой системы с помощью элементарных преобразований её матрицы:

Как видно, ранг системы равен 3, определитель системы отличен от нуля. Следовательно, однородная система трёх уравнений для трёх неизвестных имеет лишь тривиальное решение: .

Таким образом векторы линейно независимы и составляют

73

базис заданного подпространства. По определению вектор , представляющий ортогональную проекцию на подпространство , принадлежит и ортогонален . Эти условия приводят в итоге к системе уравнений для координат вектора в базисе подпространства :

где - элементы матрицы Грама.

В соответствии с формулой Крамера решение этой системы имеет вид

где - определитель матрицы Грама системы базисных векторов, а - определитель, полученный из определителя Грама заменой -го столбца на столбец из свободных членов выписанной системы уравнений.

В рассматриваемой задаче элементы матрицы Грама равны

Элементы столбца свободных членов: .

Учитывая это, для определителей имеем

Откуда .

74

Таким образом, для ортогональной прекции вектора на подпро-странство получим

Задачи

72. Найти размерность и базис ортогонального дополнения к линейной оболочке векторов:

а) , ; б) , , ;

в) , , .

72. Найти размерность и базис ортогонального дополнения к подпространству, заданному системой

а) ; б) ;

в)

72. Найти ортогональную проекцию и ортогональную составляющую вектора относительно подпространства, порожденного векторами , если

а) , , ; ;

б) , , ; .

72. Найти ортогональную проекцию и ортогональную составляющую вектора относительно подпространства, заданного системой

.

75

72. Найти ортогональную проекцию и ортогональную составляющую вектора 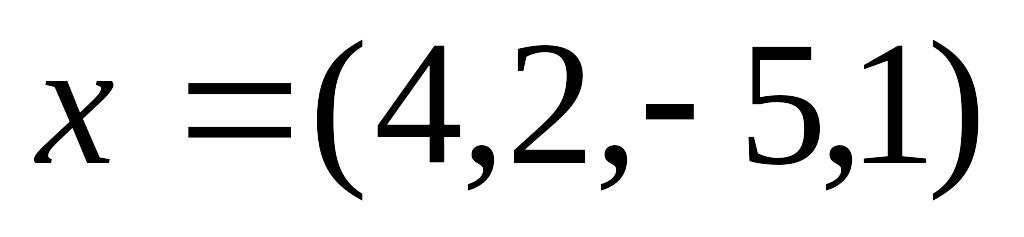относительно ортогонального дополнения к линейной оболочке векторов , .

73. Найти расстояние от вектора до подпространства L и угол между ними, если задано системой

.

72. Найти расстояние от вектора до линейной оболочки векторов , и угол между и .

73. Найти угол между вектором и подпространством, порожденным векторами , если

а) , , ;

б) , , ; .

72. Основанием -мерного параллелепипеда, построенного на векторах , служит -мерный параллелепипед, построенный на векторах . Найти объем -мерного параллелепипеда и длину перпендикуляра, опущенного на основание, если , , , .

73. Найти угол между диагональю n-мерного куба (см.задачу 3.67) и его k-мерной гранью.

76