
- •3. Линейные, евклидовы и унитарные пространства Линейные пространства
- •Доказать, что
- •Линейная зависимость и независимость векторов
- •Базис и размерность линейного пространства
- •Примеры
- •Координаты вектора
- •Линейные оболочки и подпространства
- •Евклидово пространство, ортонормированные системы
- •Примеры
- •Матрица Грама
- •Унитарное пространство
- •Ортогональное разложение векторов
Матрица Грама
Определение. Матрицей Грама для системы векторов называется симметричная матрица вида
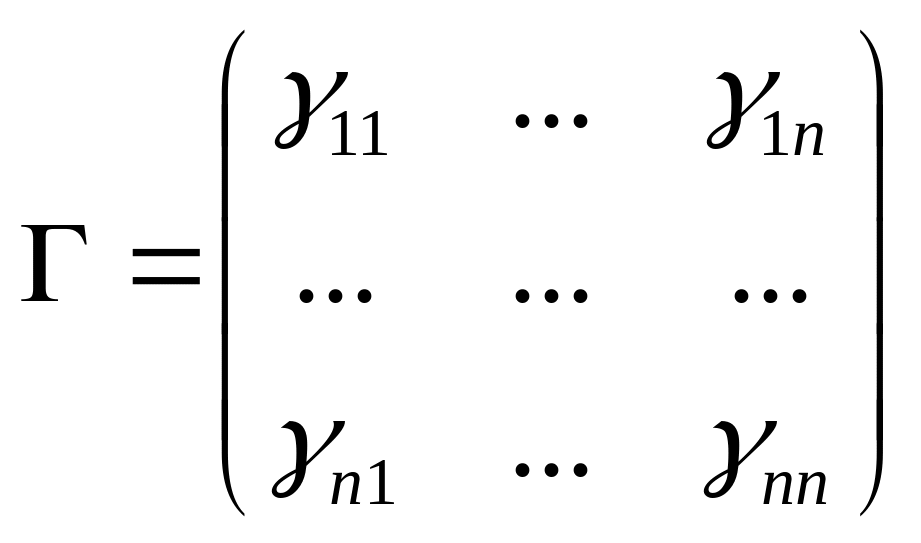 ,
,
где
![]() .
.
67
Утверждение.
Скалярное произведение векторов
![]() и
и
![]() ,
заданных в базисе
,
вычисляется по формуле
,
заданных в базисе
,
вычисляется по формуле
![]() ,
,
где
![]() - матрица Грама для системы векторов
.
- матрица Грама для системы векторов
.
Определение. Подмножество евклидова пространства Еn вида
![]() ,
,
где
![]() -
линейно независимые векторы, называется
k-мерным
параллелепипедом, построенным на
векторах
.
-
линейно независимые векторы, называется
k-мерным
параллелепипедом, построенным на
векторах
.
Утверждение. Объем k-мерного параллелепипеда, построенного на векторах , равен квадратному корню из определителя матрицы Грама для системы векторов .
Задачи
Построить матрицу Грама для системы векторов:
а)
![]() ,
,![]() ;
;
б)
![]() ,
,![]() ,
,![]() ;
;
в)
![]() ,
,![]() .
.
Вычислить скалярное произведение векторов и , заданных своими координатами в базисе , если
а)
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
б)
![]() ,
,![]() ,
,![]() ,
,
.
,
,
.
Вычислить длины векторов ,
 и угол между ними, если даны следующие
разложения по базису
и угол между ними, если даны следующие
разложения по базису
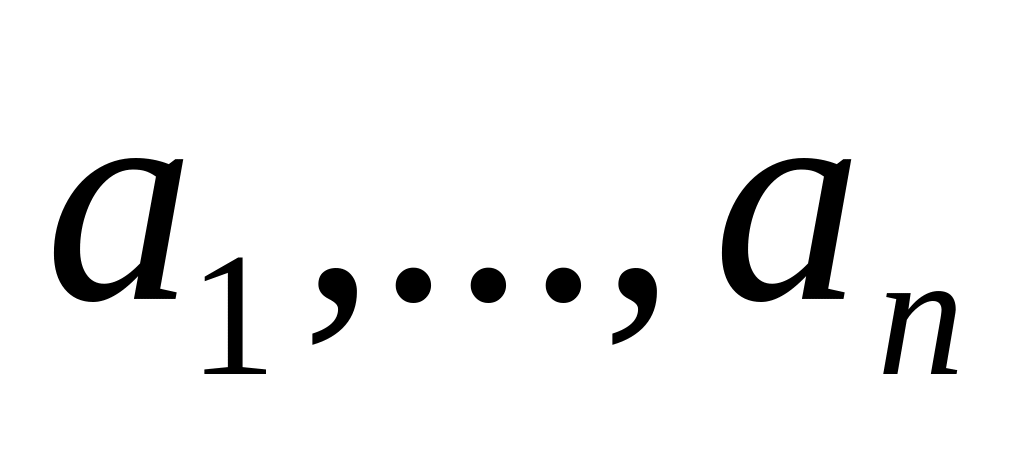 и ортонормированному базису
и ортонормированному базису
 :
:
а)
![]() ,
,![]() ,
,![]() ,
;
,
;
б)
![]() ,
,![]() ,
,
,
,![]() ;
;
68
в)
![]() ,
,![]() ,
,
,
,
,
,
![]() .
.
Найти площадь параллелограмма, построенного на векторах:
а)
,![]() ;
б)
;
б)
![]() ,
,![]() ;
;
в)
![]() ,
.
,
.
Вершины треугольника заданы своими координатами:
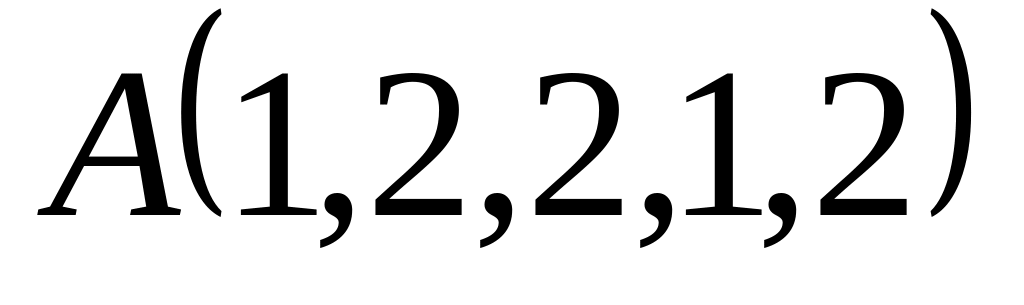 ,
,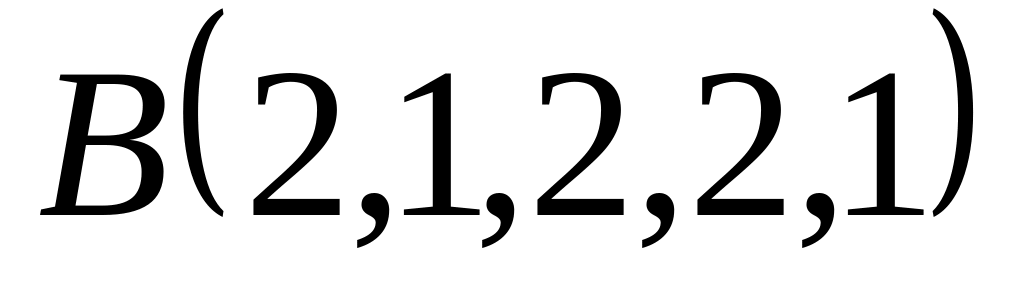 ,
,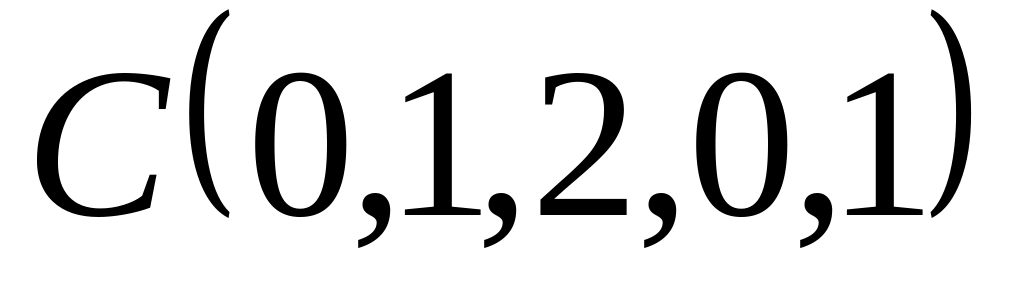 .
Найти
.
Найти
а) длину медианы, проведенной из вершины ;
б) площадь треугольника ;
в) длину высоты, опущенной из вершины .
Найти объем параллелепипеда, построенного на векторах:
а)
![]() ,
,![]() ,
,![]() ;
;
б)
![]() ,
,![]() ,
,![]() .
.
Основание параллелепипеда, построенного на векторах
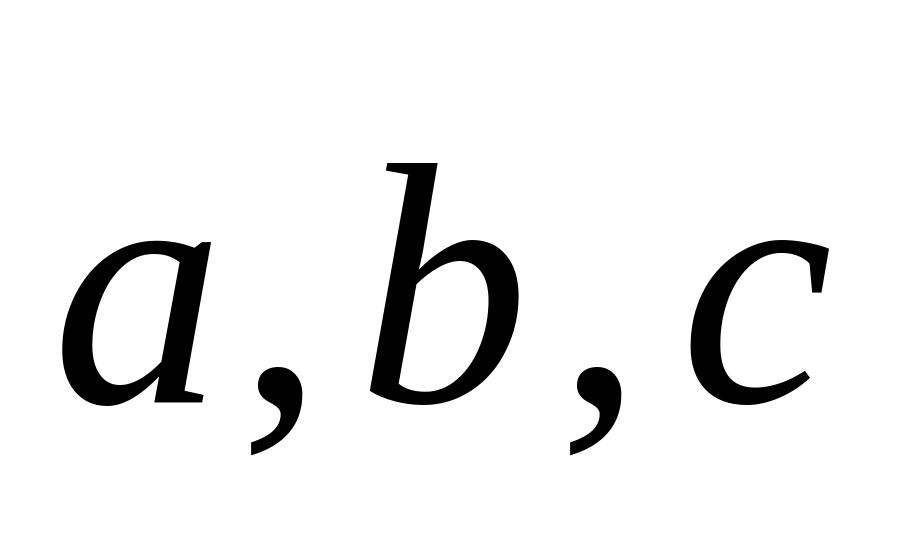 ,
лежит в плоскости векторов
,
лежит в плоскости векторов
 .
Найти высоту параллелепипеда, проведенную
к основанию, если в ортонормированном
базисе
.
Найти высоту параллелепипеда, проведенную
к основанию, если в ортонормированном
базисе
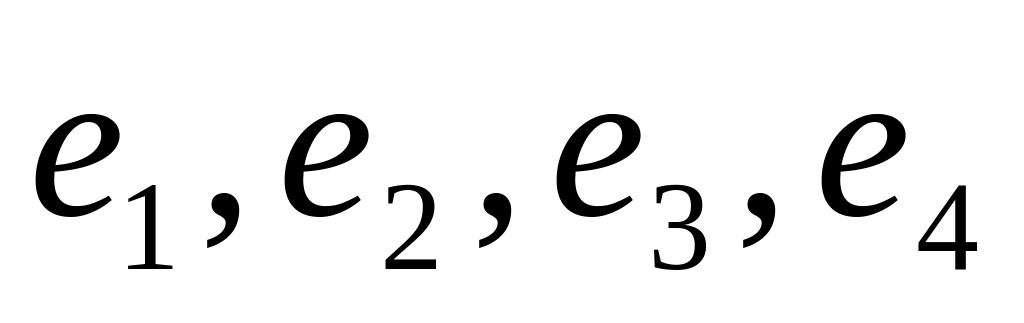 справедливо разложение
справедливо разложение
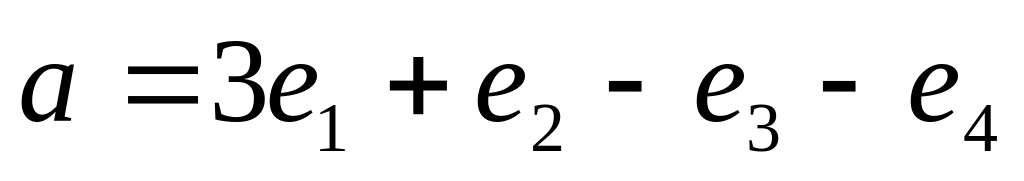 ,
,
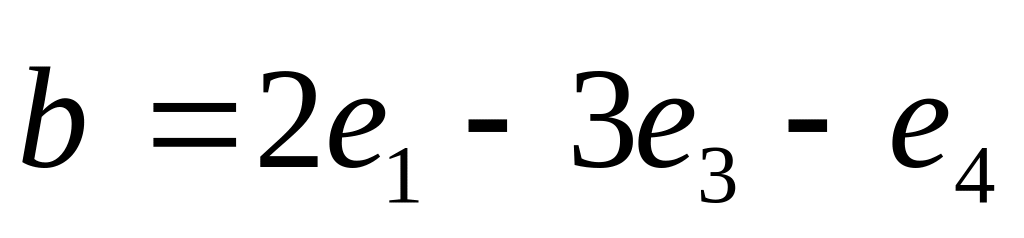 ,
,
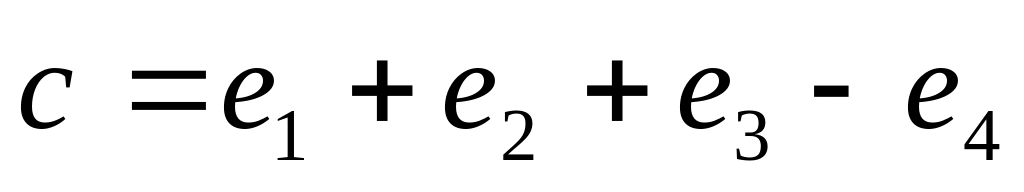 .
.Вершины пирамиды
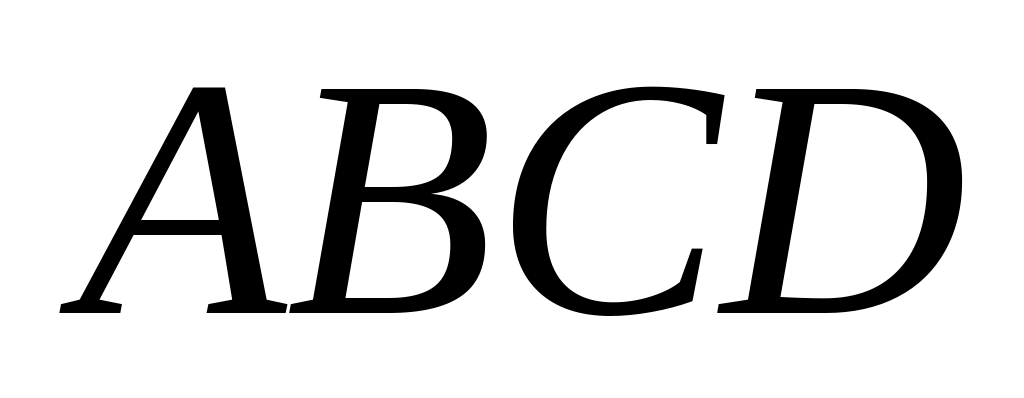 заданы своими координатами:
заданы своими координатами:
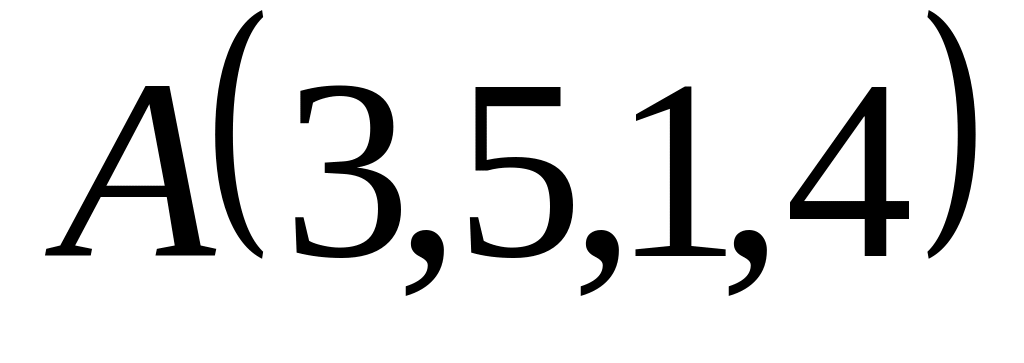 ,
,
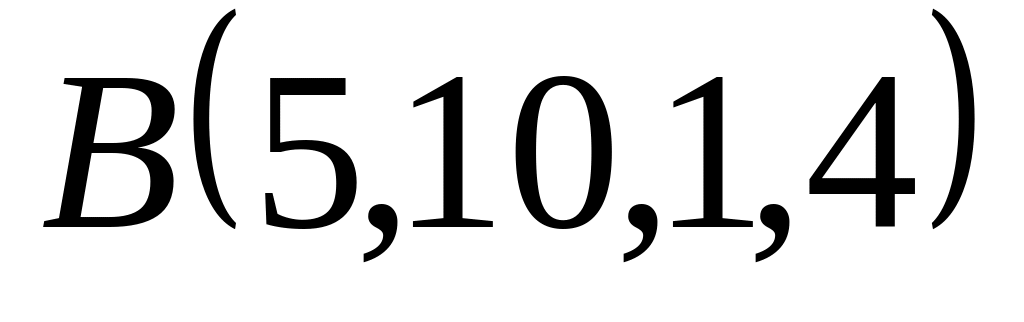 ,
,
 ,
,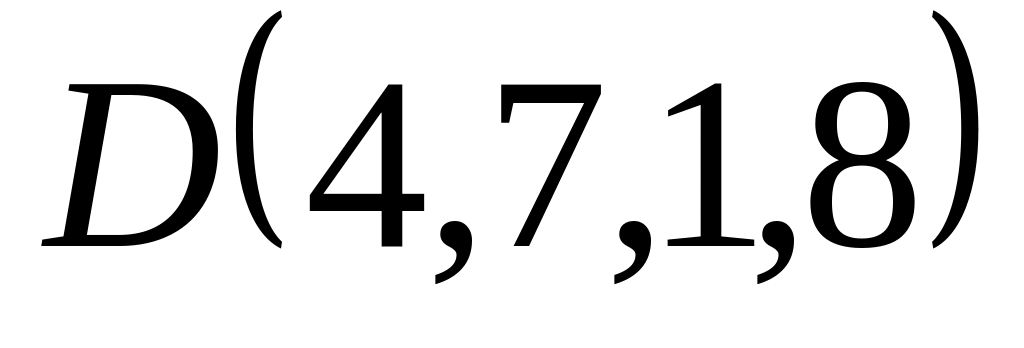 .
Найти объем пирамиды, длину высоты,
опущенной из вершины
.
Найти объем пирамиды, длину высоты,
опущенной из вершины
 на основание
,
и угол наклона бокового ребра
на основание
,
и угол наклона бокового ребра
 к плоскости основания.
к плоскости основания.
В евклидовом пространстве Еn под n-мерным единичным кубом понимается множество вида
![]() ,
,
где векторы образуют ортонормированную систему. Требуется
а) найти число диагоналей n-мерного куба;
б) найти число его диагоналей, ортогональных данной диагонали;
в) найти длину диагонали куба;
69
г) доказать, что
любая диагональ куба образует равные
углы со всеми его ребрами; найти этот
угол
![]() и его предел при
и его предел при
![]() .
.
Унитарное пространство
Определение.
Линейное пространство
называется унитарным пространством,
если каждой паре
![]() поставлено в соответствие комплексное
число, которое называется скалярным
произведением
на
,
обозначается
поставлено в соответствие комплексное
число, которое называется скалярным
произведением
на
,
обозначается
![]() ,
и для любых
,
и для любых
![]() и комплексных
и комплексных
![]() удовлетворяет следующим требованиям:
удовлетворяет следующим требованиям:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ,
причем равенство возможно лишь том
случае, когда
,
причем равенство возможно лишь том
случае, когда
![]() .
.
Утверждение. Комплексное линейное пространство
Un=![]() ,
,
в котором скалярное произведение векторов задано равенством
![]() ,
,
является унитарным пространством.
Примеры
Векторы образуют ортонормированный базис в унитарном пространстве. Найти скалярное произведение
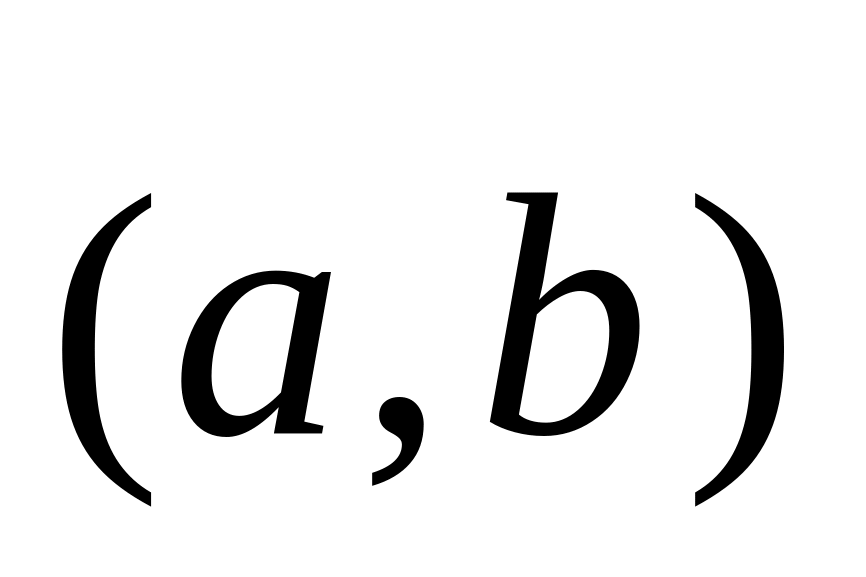 ,
если
,
если
![]() .
.
Решение.
В рассматриваемом случае в соответствии
со свойствами скалярного произведения
в унитарном пространстве можно записать
![]()
В унитарном пространстве со скалярным произведением
70
вида
![]() построить ортонормированный базис по
данному
построить ортонормированный базис по
данному
![]() .
.
Решение. Сначала проведём процедуру ортогонализации. В данном случае она аналогична описанной для евклидова пространства. Положим
![]() .
.
Используя условия ортогональности, получим
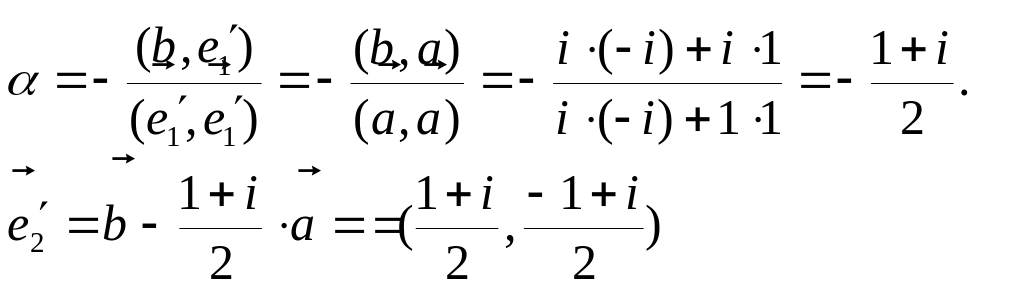 .
.
Теперь
отнормируем векторы
![]() :
:
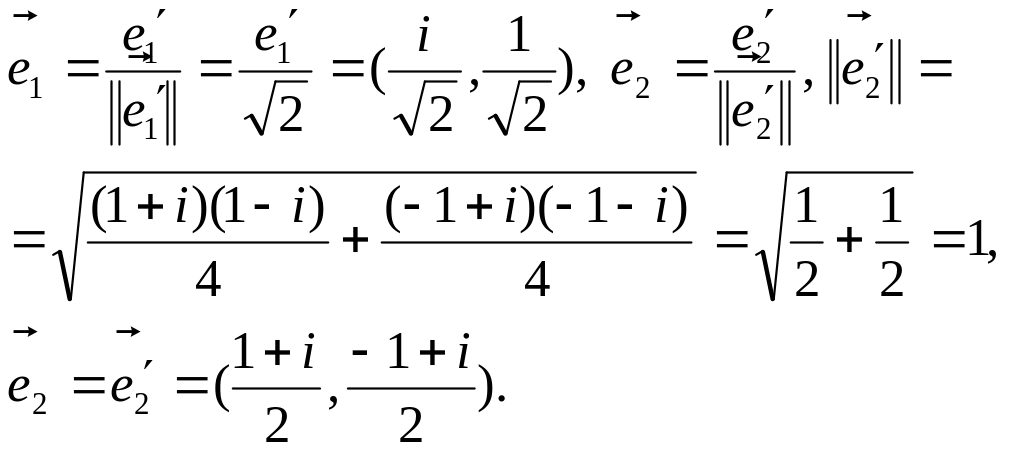
Задачи
В унитарном пространстве Un вычислить скалярное произведение:
а)
![]() на
на
![]() ;
б)
;
б)
![]() на
на
![]() ;
;
в)
![]() на
на
![]() ;
г)
;
г)
![]() на
на
![]() .
.
Ортогональны ли векторы:
а)
![]() и
и
![]() ;
б)
;
б)
![]() и
и
![]() ;
;
в)
![]() и
и
![]() .
.
В унитарном пространстве Un вычислить норму вектора:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
3.71. Построить матрицу Грама системы векторов:
а)
![]() ,
,![]() ,
,![]() ; б)
; б)
![]() ,
,![]() .
.
71
Векторы
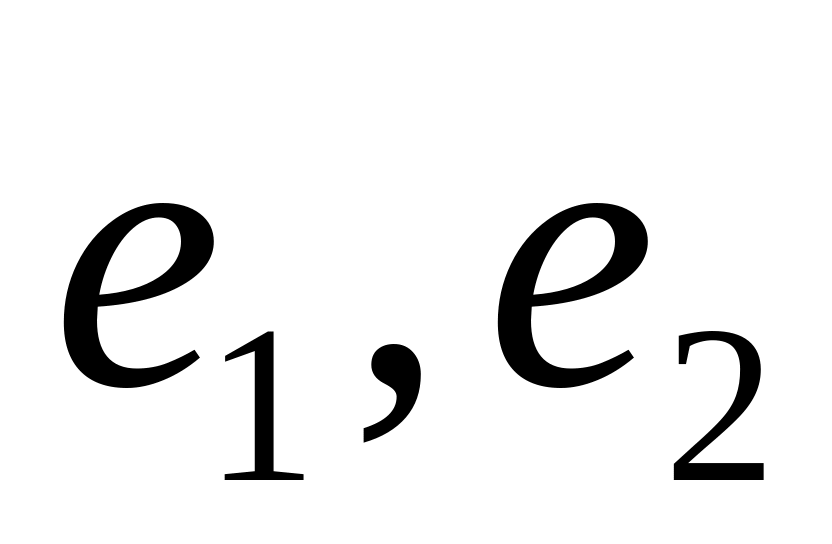 образуют ортонормированный базис
пространства U2.
Найти скалярное произведение
образуют ортонормированный базис
пространства U2.
Найти скалярное произведение
 и
и
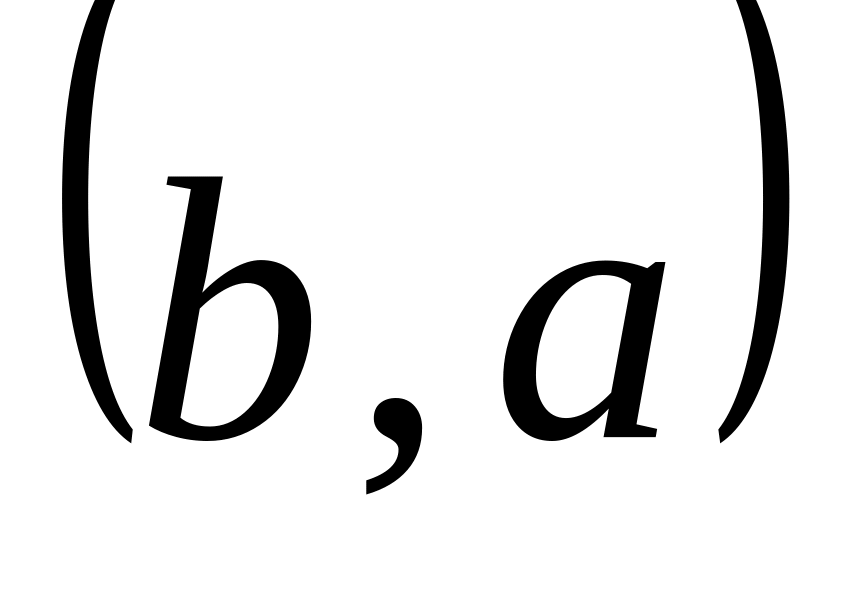 ,
если
,
если
а)
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() .
.
Векторы образуют ортогональный базис пространства U2. Найти и
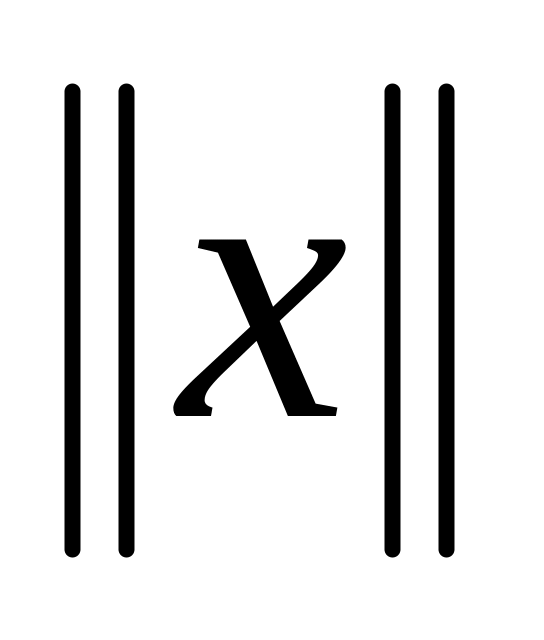 ,
если
,
если
а)
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
б)
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ортонормировать систему векторов:
а)
![]() ,
,![]() ;
б)
;
б)
![]() ,
,![]() .
.
Показать, что линейное пространство
![]()
не
будет являться унитарным, если в нем
скалярное произведение
![]() на
на
![]() задать равенством
задать равенством
![]() .
.
