
- •3. Линейные, евклидовы и унитарные пространства Линейные пространства
- •Доказать, что
- •Линейная зависимость и независимость векторов
- •Базис и размерность линейного пространства
- •Примеры
- •Координаты вектора
- •Линейные оболочки и подпространства
- •Евклидово пространство, ортонормированные системы
- •Примеры
- •Матрица Грама
- •Унитарное пространство
- •Ортогональное разложение векторов
Базис и размерность линейного пространства
Определение.
Базисом линейного пространства
называется линейно
независимая система векторов
![]() из
такая, что любой
вектор из пространства
можно
представить в
виде линейной комбинации векторов
.
из
такая, что любой
вектор из пространства
можно
представить в
виде линейной комбинации векторов
.
Определение.
Размерностью линейного пространства
называется
количество векторов в базисе этого
пространства. Обозначается
![]() .
.
Утверждение. Базисом линейного пространства решений однородной системы является ее фундаментальная система решений.
Утверждение. Rn=n.
Примеры
Образуют ли базис в пространстве R3 векторы
![]() ?
?
Решение. По определению базис составляют линейно независимые векторы. Линейная зависимость (или независимость) определяется исходя из анализа равенства нулю линейной комбинации этих векторов:
![]() .
.
Последнее
векторное уравнение после записи его
по компонентам представляет собой
систему трёх однородных уравнений
относительно
![]() .
Согласно схеме исследования линейной
зависимости векторов (см. пример 1 из
раздела «Линейная зависимость и
независимость векторов») вычислим
определитель матрицы, составленной из
координат векторов
.
Согласно схеме исследования линейной
зависимости векторов (см. пример 1 из
раздела «Линейная зависимость и
независимость векторов») вычислим
определитель матрицы, составленной из
координат векторов

48
Определитель системы равен нулю, следовательно, она имеет нетривиальное решение и это означает, что исходная группа векторов линейно зависима и не образует базис в R3.
Найти размерность и один из базисов линейного пространства решений однородной системы:
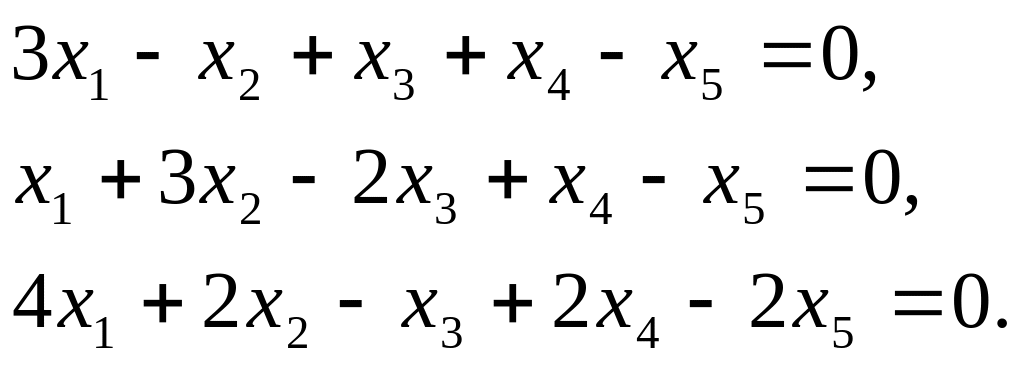
Решение. Представленная система состоит из трёх уравнений и содержит 5 неизвестных. Выпишем матрицу системы и упростим её с помощью элементарных преобразований, сначала поменяв местами строки 1 и 2, а затем вычитая новую первую строку, умноженную на 3 и 4, соответственно из второй и третьей строк :
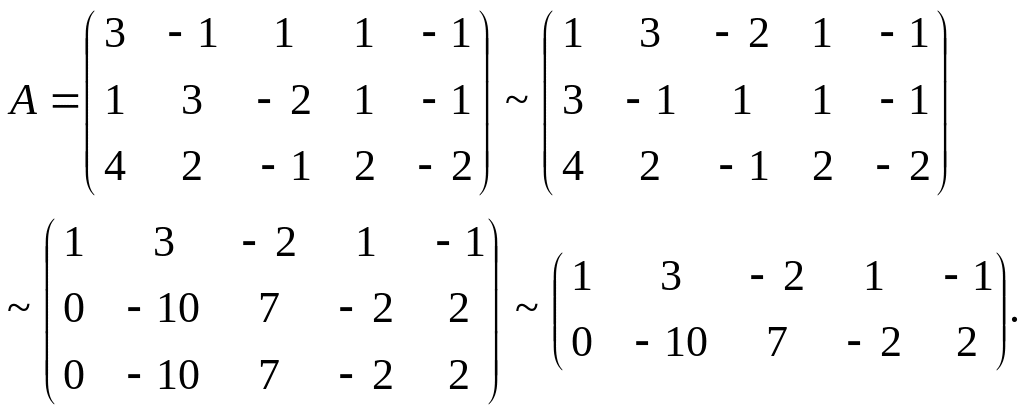
Видно
что ранг матрицы
равен 2. Следовательно, две неизвестные
являются главными, а три - свободными.
Значит ФСР системы содержит 5-2=3 линейно
независимых решения. Выберем в качестве
главных
![]() .
Это можно сделать, т.к. минор 2-го порядка,
составленный из коэффициентов при этих
неизвестных, отличен от нуля. Система,
соответствующая преобразованной
матрице, имеет вид
.
Это можно сделать, т.к. минор 2-го порядка,
составленный из коэффициентов при этих
неизвестных, отличен от нуля. Система,
соответствующая преобразованной
матрице, имеет вид
![]()
Отсюда, выражая главные неизвестные через свободные, получим общее решение
![]()
49
Или иначе:
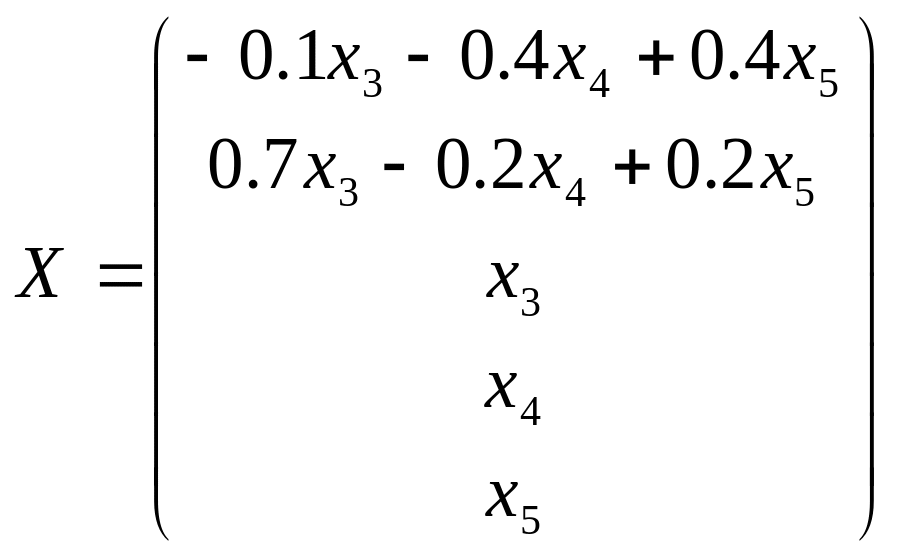 .
.
Фундаментальная совокупность решений, составленная в соответствии с изложенным алгоритмом (см. пример 4 в разделе «Системы линейных алгебраических уравнений»), является базисом линейного пространства решений исходной системы и в данном случае имеет вид
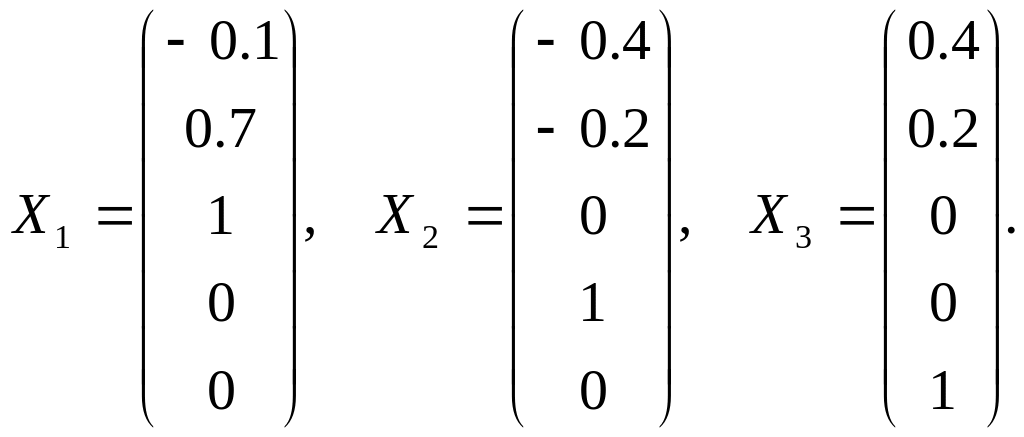
Размерность искомого пространства равна 3.
Задачи
Является ли базисом пространства R3 система векторов:
а)
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() ;
;
в)
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найти размерность и базис пространства решений однородной системы:
а)
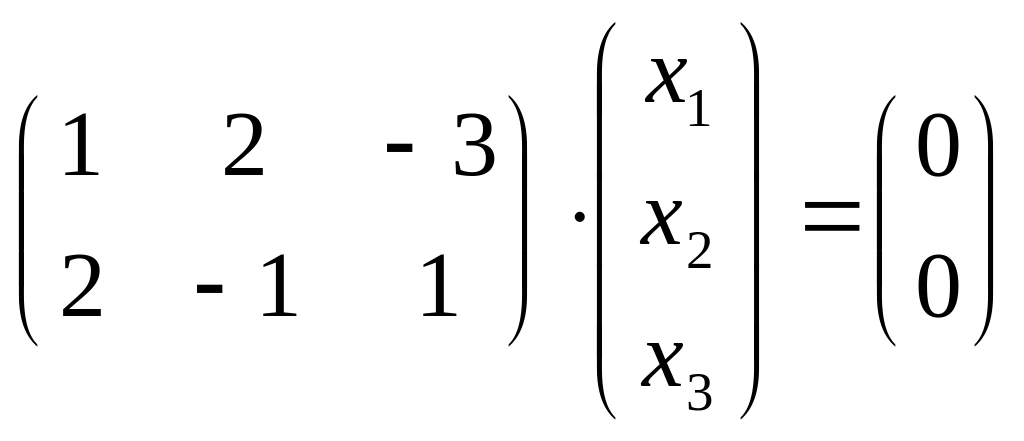 ;
б)
;
б)
![]() ;
;
50
в)
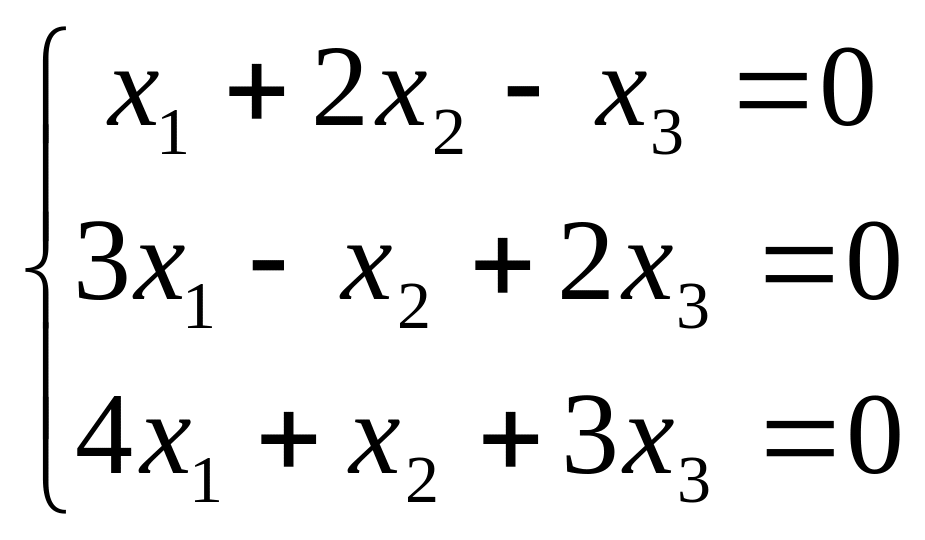 ;
г)
;
г)
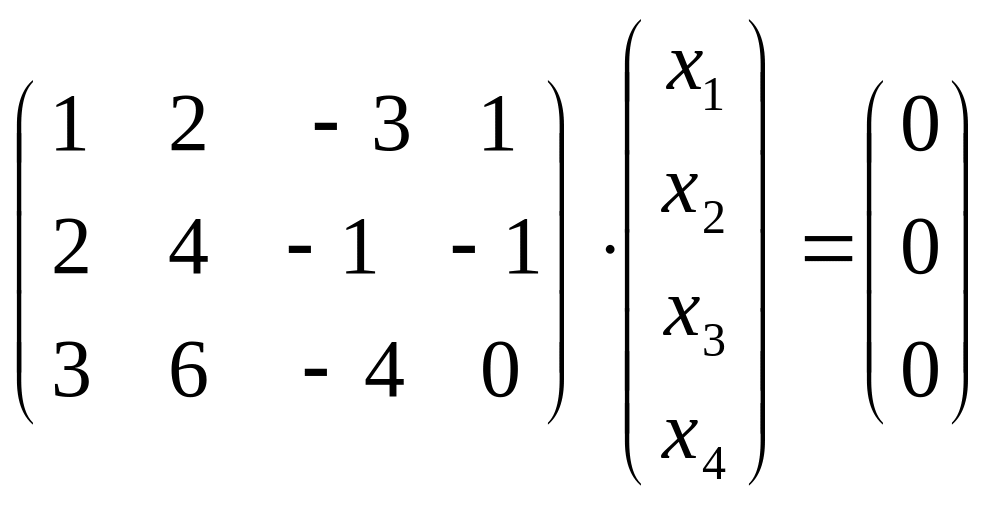 ;
;
д)
![]() .
.
Найти размерность и указать какой-либо базис пространства всех векторов, выходящих из начала координат и:
а) лежащих на прямой
![]() ;
;
б) перпендикулярных
прямой
![]() ;
;
в) лежащих в плоскости
![]() ;
;
г) перпендикулярных
плоскости
![]() .
.
Вектор
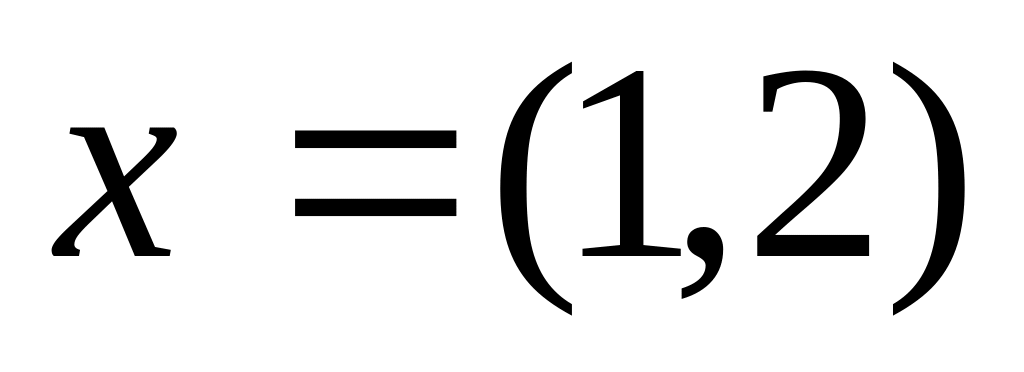 разложить по базису
разложить по базису
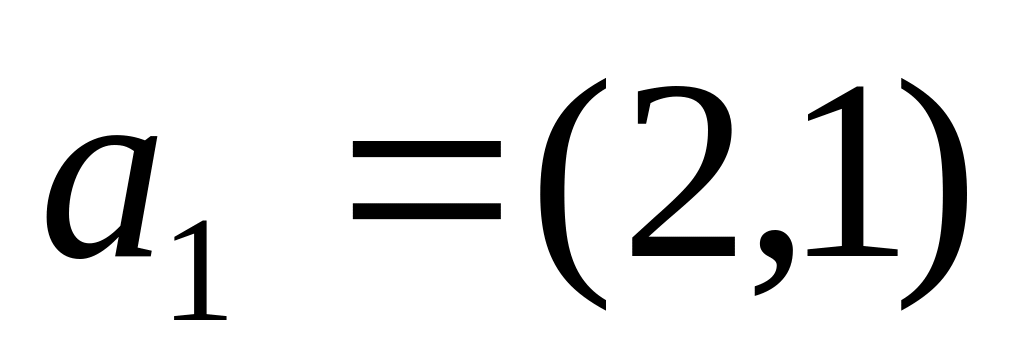 ,
,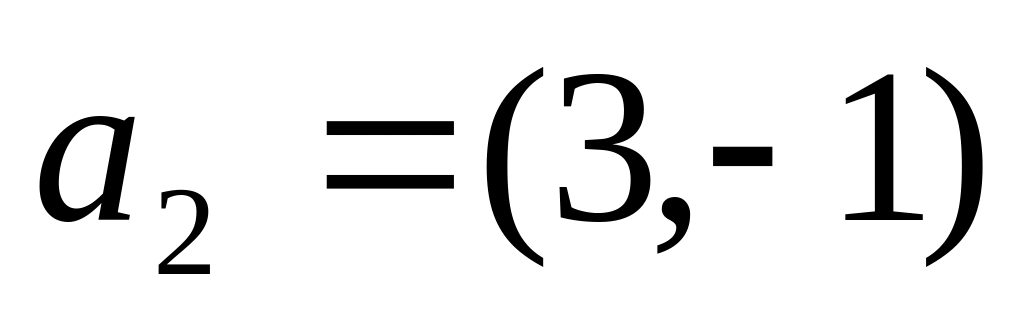 .
.Данный вектор разложить по указанному базису
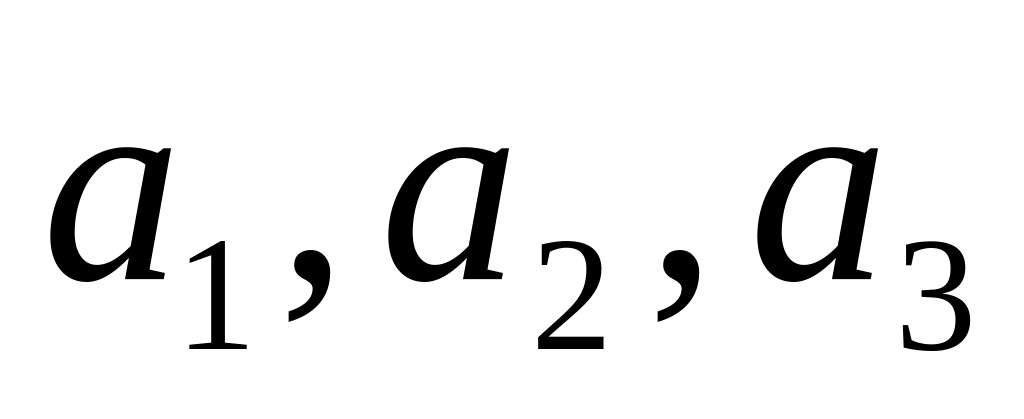 :
:
а)
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
б)
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Дополнить до какого-либо базиса соответствующего пространства Rn систему:
а)
![]() ,
,![]() ;
;
б)
![]() ,
,![]() ,
,![]() ;
;
в)
![]() ,
,![]() .
.
При каких значениях параметра
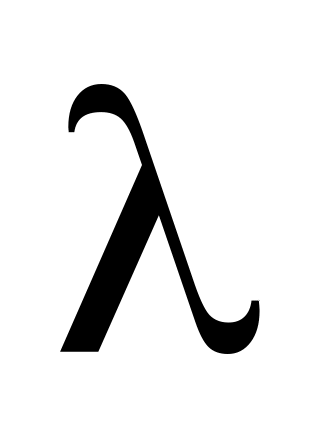 векторы образуют базис пространства
R3:
векторы образуют базис пространства
R3:
а)
![]() ,
,![]() ,
,![]() ;
;
б)
![]() ,
,![]() ,
,![]() ;
;
в)
![]() ,
,![]() ,
,![]() .
.
51
Найти размерность и указать какой-либо базис пространства:
а) многочленов степени не выше n;
б) квадратных матриц порядка n;
в) прямоугольных
матриц размера
![]() ;
;
г) симметричных матриц порядка n;
д) диагональных матриц порядка n.
Доказать, что система
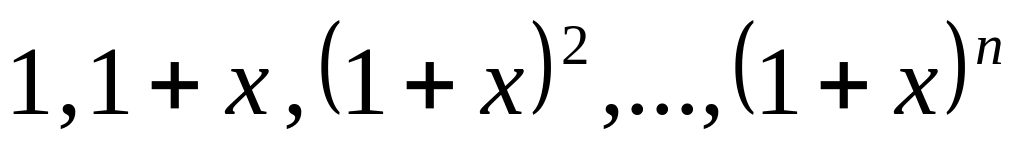 образует базис
образует базис
пространства многочленов степени не выше n.
Найти размерность и указать какой-либо базис пространства положительных чисел, в котором сумма произвольных чисел и вычисляется как
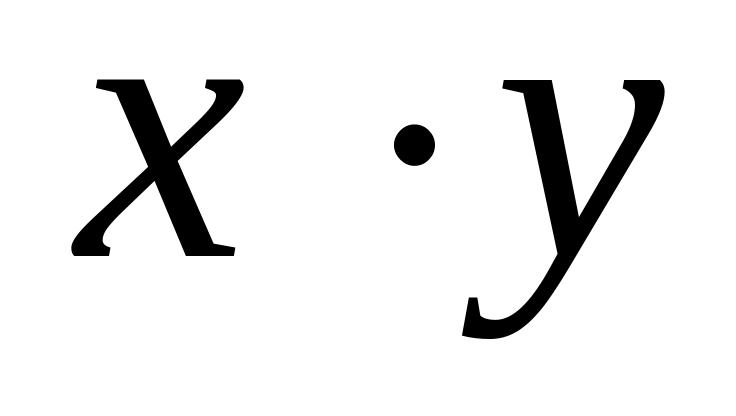 ,
а произведение вещественного числа
на произвольное положительное число
,
а произведение вещественного числа
на произвольное положительное число
 вычисляется как
вычисляется как
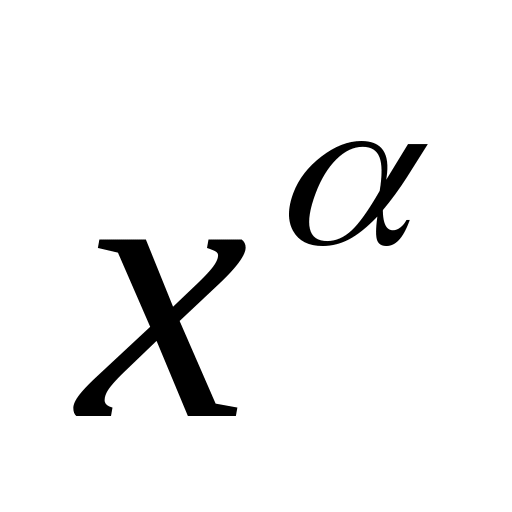 .
.
