
- •3. Линейные, евклидовы и унитарные пространства Линейные пространства
- •Доказать, что
- •Линейная зависимость и независимость векторов
- •Базис и размерность линейного пространства
- •Примеры
- •Координаты вектора
- •Линейные оболочки и подпространства
- •Евклидово пространство, ортонормированные системы
- •Примеры
- •Матрица Грама
- •Унитарное пространство
- •Ортогональное разложение векторов
3. Линейные, евклидовы и унитарные пространства Линейные пространства
Определение.
Множество векторов
![]() называется вещественным линейным
пространством, если в этом множестве
введены операции сложения двух
векторов (т.е. каждой паре
называется вещественным линейным
пространством, если в этом множестве
введены операции сложения двух
векторов (т.е. каждой паре
![]() ,
,![]() поставлен в соответствие определенный
элемент
поставлен в соответствие определенный
элемент
![]() из множества
)
и умножения вектора на вещественное
число (т.е. каждому вектору
из множества
)
и умножения вектора на вещественное
число (т.е. каждому вектору
![]() и произвольному
числу
и произвольному
числу
![]() поставлен в соответствие определенный
элемент
поставлен в соответствие определенный
элемент
![]() из множества
),
и эти две операции удовлетворяют
следующим аксиомам:
из множества
),
и эти две операции удовлетворяют
следующим аксиомам:
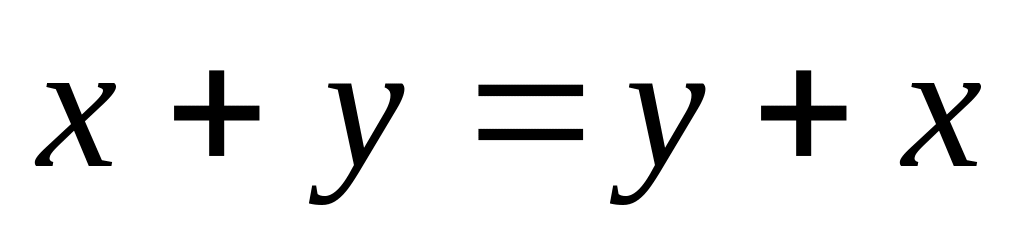 для
для
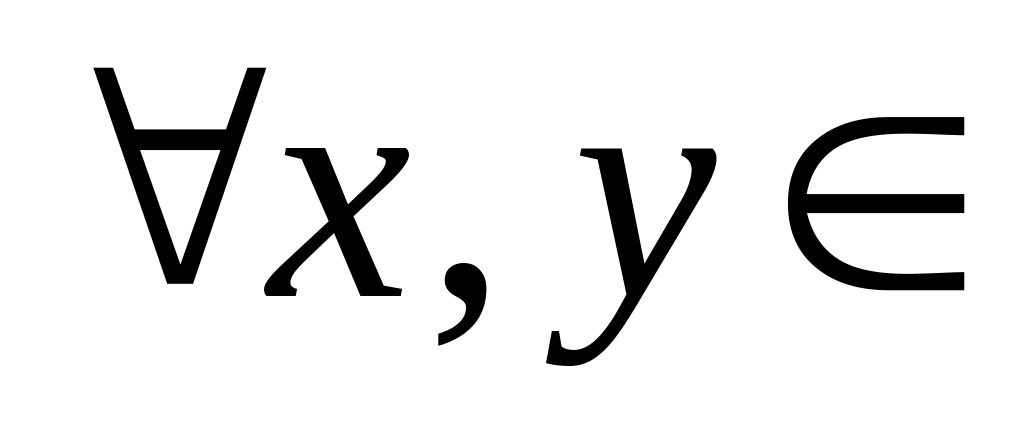 ;
;
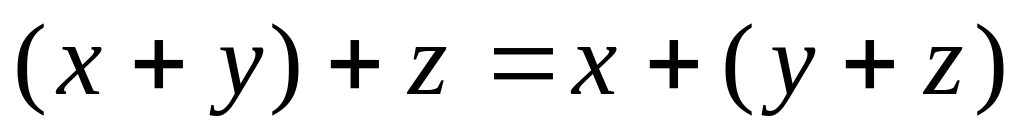 для
для
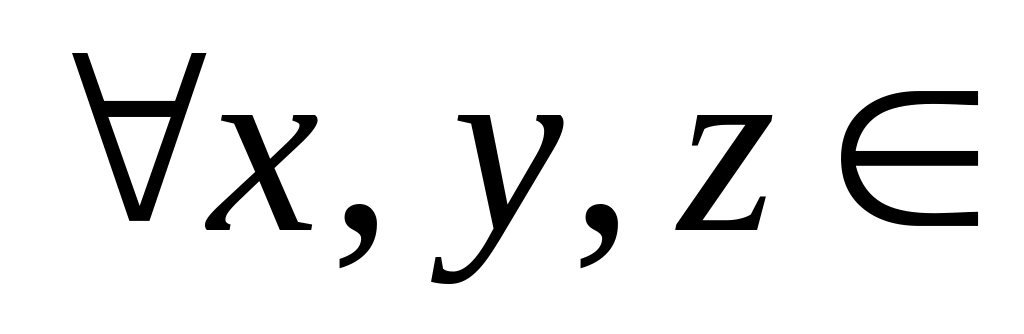 ;
;во множестве существует нулевой вектор
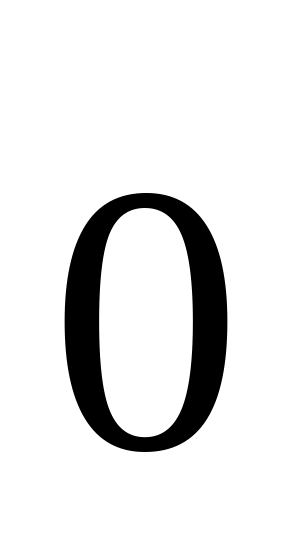 такой, что
такой, что
 для
для
 ;
;для во множестве существует противоположный вектор
 такой, что
такой, что
 ;
;для выполняется
 ;
;для
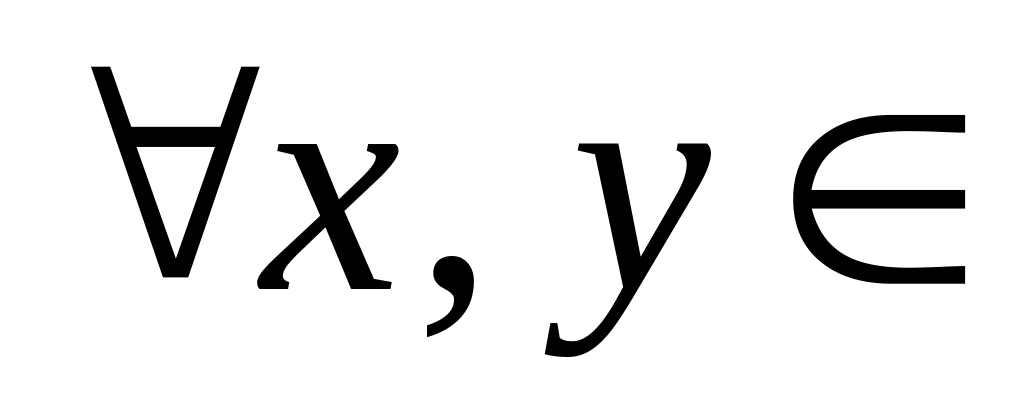 и
и
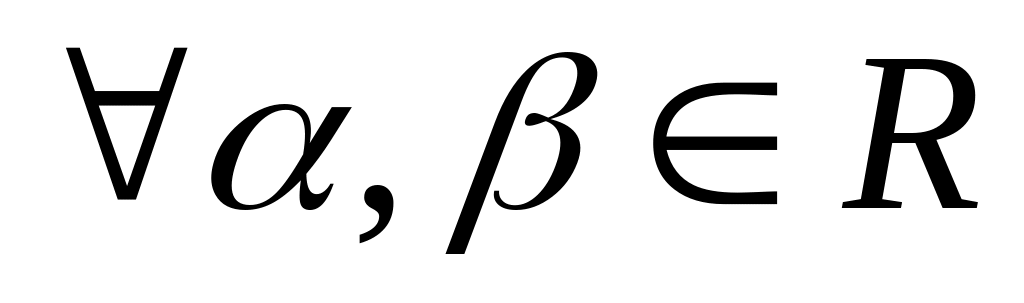 выполняются равенства
выполняются равенства
![]() ;
;
![]() ;
;
![]() .
.
Определение.
Арифметическим пространством Rn
называется
множество векторов
![]() ,
в котором операции сложения векторов
и умножения вектора на число определены
следующим образом: если
,
,
в котором операции сложения векторов
и умножения вектора на число определены
следующим образом: если
,![]() ,
,![]() ,
то
,
то
![]() ,
,![]() .
.
41
Утверждение. Множество всех решений однородной системы образует
линейное пространство.
Определение.
Линейной комбинацией
векторов
![]() называется сумма вида
называется сумма вида
![]() ,
где
,
где
![]() -
произвольные числа.
-
произвольные числа.
Утверждение. Множество всех линейных комбинаций векторов образует линейное пространство.
Задачи
Доказать, что следующее множество является линейным пространством, указать его нулевой элемент, а также какой-либо конкретный элемент этого пространства и противоположный ему элемент:
а) множество решений
однородной системы
![]() ;
;
б) множество решений
однородной системы
![]() ;
;
в) множество всех квадратных матриц n-го порядка;
г) множество всех симметричных матриц n-го порядка;
д) множество всех векторов, лежащих на одной оси;
е) множество всех
линейных комбинаций векторов
![]() R3.
R3.
Доказать, что множество всех решений однородной системы образует линейное пространство.
Доказать, что множество всех линейных комбинаций векторов образует линейное пространство.
Является ли линейным пространством множество
а) всех решений неоднородной совместной системы линейных уравнений;
42
б) всех векторов координатной плоскости, каждый из которых лежит на одной из координатных осей;
в) всех многочленов степени не выше n;
г) всех многочленов n-ой степени;
д) всех сходящихся числовых последовательностей;
е) всех числовых
последовательностей![]() ,
сходящихся к даному числу
,
сходящихся к даному числу
![]() .
.
Доказать, что
а) множество всех
непрерывных функций, заданных на отрезке
![]() ,
где сумма произвольных функций
,
где сумма произвольных функций
![]() и
и
![]() вычисляется как
вычисляется как
![]() ,
а произведение функции на число
вычисляется обычным образом, не является
линейным пространством;
,
а произведение функции на число
вычисляется обычным образом, не является
линейным пространством;
б) множество всех
векторов пространства R3,
где сумма произвольных векторов
![]() и
и
![]() вычисляется как
вычисляется как
![]() ,
а произведение вектора на число
вычисляется обычным образом, не
является линейным пространством;
,
а произведение вектора на число
вычисляется обычным образом, не
является линейным пространством;
в) множество всех
диагональных матриц n-го
порядка, где сумма произвольных матриц
![]() и
и
![]() вычисляется как
вычисляется как
![]() ,
а произведение матрицы на число
вычисляется обычным образом, не является
линейным пространством;
,
а произведение матрицы на число
вычисляется обычным образом, не является
линейным пространством;
г) множество всех
вещественных чисел, в котором сумма
произвольных чисел
![]() и
и
![]() вычисляется как
вычисляется как
![]() ,
а произведение числа на число
вычисляется обычным образом, не является
линейным пространством.
,
а произведение числа на число
вычисляется обычным образом, не является
линейным пространством.
