1. Машина - техническое устройство, выполняющее преобразование энергии, материалов и информации с целью облегчения физического и умственного труда человека, повышения его качества и производительности.
В этом определении под материалами понимаются обрабатываемые предметы, перемещаемые грузы и другие объекты труда. В зависимости от основного назначения (какой вид преобразования преобладает) различают энергетические, технологические, транспортные и информационные машины.
Энергетические машины предназначены для преобразования любого вида энергии в механическую (и наоборот). К ним принадлежат, например, электродвигатели, турбины, двигатели внутреннего сгорания, паровые машины, электрогенераторы.
Машины для преобразования материалов подразделяются на технологические и транспортные. В технологических машинах под материалом подразумевается обрабатываемый предмет, который может быть в твердом, жидком и газообразном виде. Преобразование материала в этих машинах состоит в изменении его размеров, формы, свойств или состояния. Примеры технологических машин: металлообрабатывающие станки, прокатные станы, ткацкие станки, упаковочные машины. В транспортных машинах под материалом понимается перемещаемый предмет. Примеры транспортных машин: автомобили, тепловозы, самолеты, вертолеты, подъемники, краны, транспортеры. В тех случаях, когда транспортная машина предназначена для перемещения людей, под материалом, конечно, понимается кабина лифта, вагон, шасси автомобиля и т. п.
Машины, предназначенные для получения и преобразования информации, называются информационными. Если информация представлена в виде чисел, то информационная машина называется счетной или вычислительной. Примеры счетных машин: арифмометры, механические интеграторы, бухгалтерские машины. Электронная вычислительная машина, строго говоря, не является машиной, так как в ней механические движения служат лишь для выполнения вспомогательных операций.
Итак, основным признаком, отличающим машину от других устройств, является выполнение механических движений (В машинах могут быть и другие виды движения, например тепловые, но они -не служат определяющим признаком, т. е.. их наличие или отсутствие не влияет на определение термина.) — отсюда и происходит термин «машина». Однако из всех устройств, имеющих движущиеся части, только те могут быть названы машинами, в которых механические движения предназначены для преобразования энергии, материалов и информации.
Машина, в которой все преобразования энергии, материалов и информации выполняются без непосредственного участия человека, называется машиной-автоматом. Применение машин-автоматов, однако, предполагает присутствие человека (оператора), наблюдающего за их работой и изменяющего в необходимых случаях программу действия. Совокупность машин-автоматов, соединенных между собой автоматическими транспортными устройствами и предназначенных для выполнения определенного технологического процесса, образует автоматическую линию. Машина, особенно машина-автомат, при правильном ее использовании облегчает труд человека, увеличивает производительность труда и обеспечивает высокое качество выполнения рабочего процесса.
2. Механизм
В учебной литературе используются несколько определений механизма:
Первое: Механизмом называется система твердых тел, предназначенная для передачи и преобразования заданного движения одного или нескольких тел в требуемые движения других твердых тел [4, 12].
Второе: Механизм - кинематическая цепь, в состав которой входит неподвижное звено (стойка) и число степеней, свободы которой равно числу обобщенных координат, характеризующих положение цепи относительно стойки [1, 3, 5, 6].
Третье: Механизмом называется устройство для передачи и преобразования движений и энергий любого рода [13].
Четвертое: Механизм - система твердых тел, подвижно связанных путем соприкосновения и движущихся определенным, требуемым образом относительно одного из них, принятого за неподвижное [14].
Всякий механизм состоит из отдельных тел (деталей), соединенных между собой.
Деталь – это изделие, изготовленное без сборочных операций.
Детали, соединенные между собой неподвижно или с помощью упругих связей, образуют отдельное звено.
Выполнение звеньев из нескольких деталей обеспечивается их соединением. Различают соединения неразъемные (сварные, заклепочные, клеевые) и разъемные (шпоночные, шлицевые, резьбовые).
Звенья в зависимости от вида их материала могут быть твердые и гибкие (упругие).
Два звена, соединенных друг с другом подвижно, образуют кинематическую пару.
Неподвижное звено, состоящее из одной или нескольких деталей, называется стойкой.
Таким образом, каждый механизм имеет стойку и подвижные звенья, среди которых выделяют входные, выходные и промежуточные звенья.
Входным (ведущим) звеньям сообщается движение, преобразуемое механизмом в требуемые движения выходных (ведомых) звеньев с помощью промежуточных звеньев. Обычно в механизме имеется одно входное и выходное звено. Но в некоторых случаях имеют место механизмы с несколькими входными или выходными звеньями, например, дифференциал автомобиля.
Развитие техники осуществляется в направлении совершенствования ранее известных механизмов и путем создания принципиально новых их видов.
Число степеней свободы или подвижность механизма - число независимых обобщенных координат однозначно определяющее положение всех его звеньев на плоскости или в пространстве.
Кинематические цепи и их классификация
Любой механизм представляет собой кинематическую цепь (к.ц.) звеньев, соединенных в кинематические пары (к.п.). К.ц. могут быть простыми и сложными, открытыми и замкнутыми, плоскими и пространственными.
В простой к.ц. каждое из ее звеньев входит в состав одной или двух к.п., а в сложной к.ц. имеются звенья, входящие в состав трех и более к.п.
В открытой к.ц. имеются звенья, входящие в состав одной к.п., а в замкнутой цепи каждое звено входит в состав 2-х и более к.п. (рис.3,а-в).
Если точки всех звеньев двигаются в одной или параллельных плоскостях, то к.ц. называется плоской, в противном случае к.ц. – пространственная (точки звеньев описывают плоские кривые в непараллельных плоскостях или пространственные).
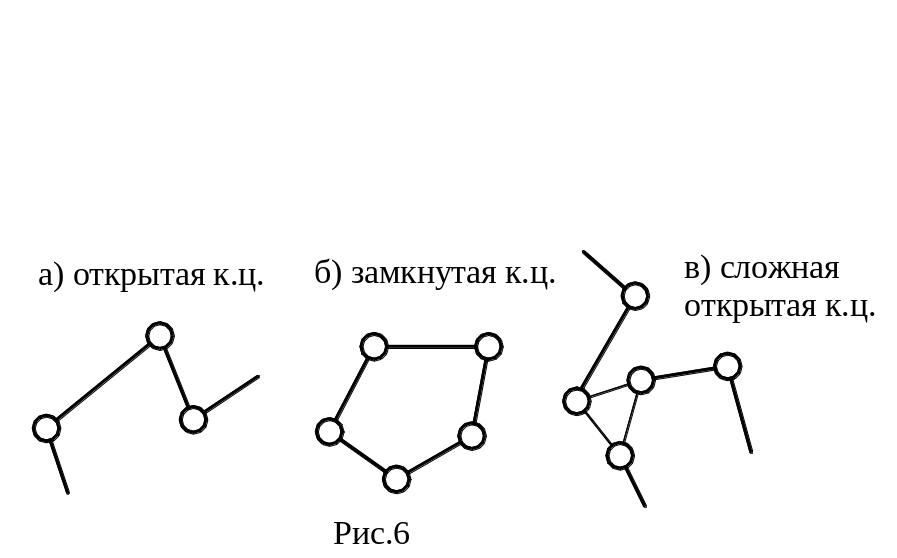
Рис.3
3. Кинематические пары
Кинематические пары (к.п.) классифицируются по разным признакам, например, по характеру соприкосновения звеньев – на низшие, когда контакт происходит по поверхности, и высшие, когда контакт звеньев осуществляется по линии или в точке.
Преимуществом низших к.п. является возможность передачи значительных усилий при малом износе, а достоинством высших к.п. возможность воспроизводить достаточно сложные относительные движения.
Рисунок 1
Низшие к.п. могут быть поступательными, вращательными, плоскими и пространственными, а также классифицироваться по числу условий связи, накладываемых на звенья при соединении их в к.п.
Любое тело в декартовой системе координат (рисунок 1) имеет 6 степеней свободы или подвижности (W=6), часть из которых уничтожается в к.п., при этом класс к.п. определяется числом накладываемых связей (6-S),
где S – число относительных движений звеньев в к.п.
Например, на рисунках приведены к.п. различных классов.
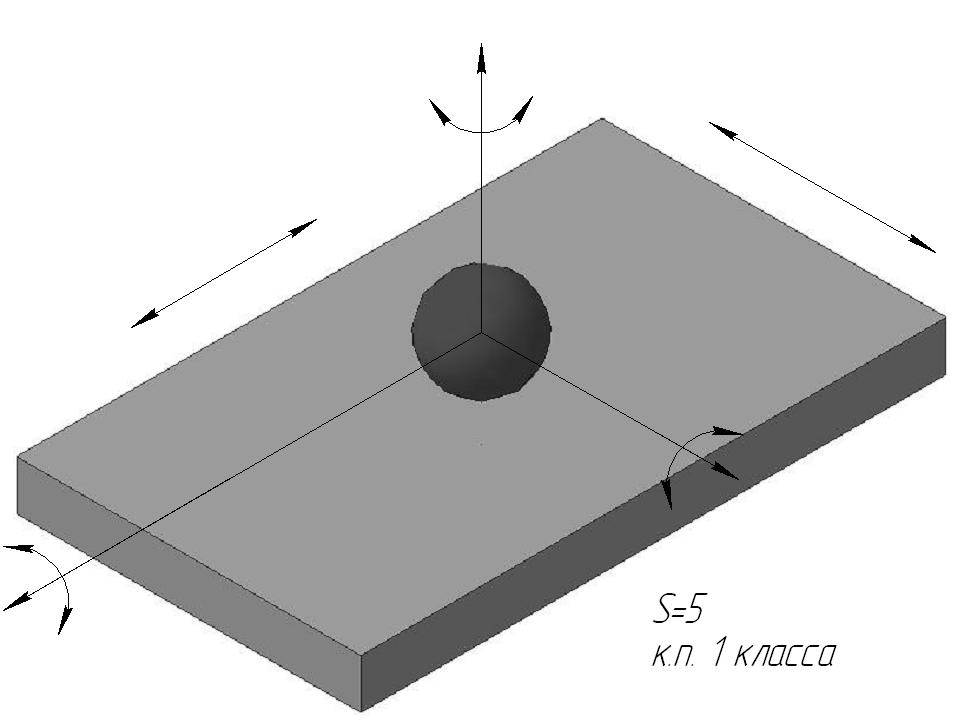
«шар — плоскость» число связей равно 1 (одно ограничение — невозможность относительного перемещения по нормали к плоскости). Следовательно, суммируя число степеней свободы и число связей, получаем 5+1=6. На этом основании пятиподвижную кинематическую пару можно назвать также парой с одной связью или парой первого класса, если считать, что номер класса пары совпадает с числом связей.
Аналогично, четырехподвижная пара «цилиндр — плоскость» имеет 4 степени свободы и 2 связи, т. е. она относится к парам второго класса.
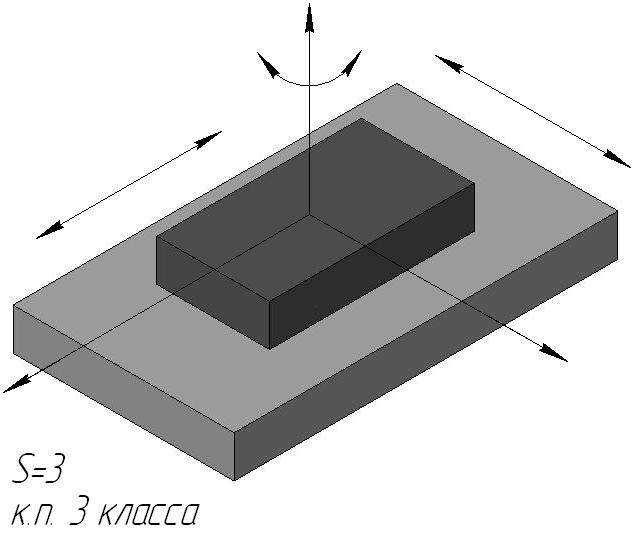
в
Трехподвижные кинематические пары (пары третьего класса) представлены в двух вариантах: плоскостная пара и сферическая пара (шаровой шарнир).
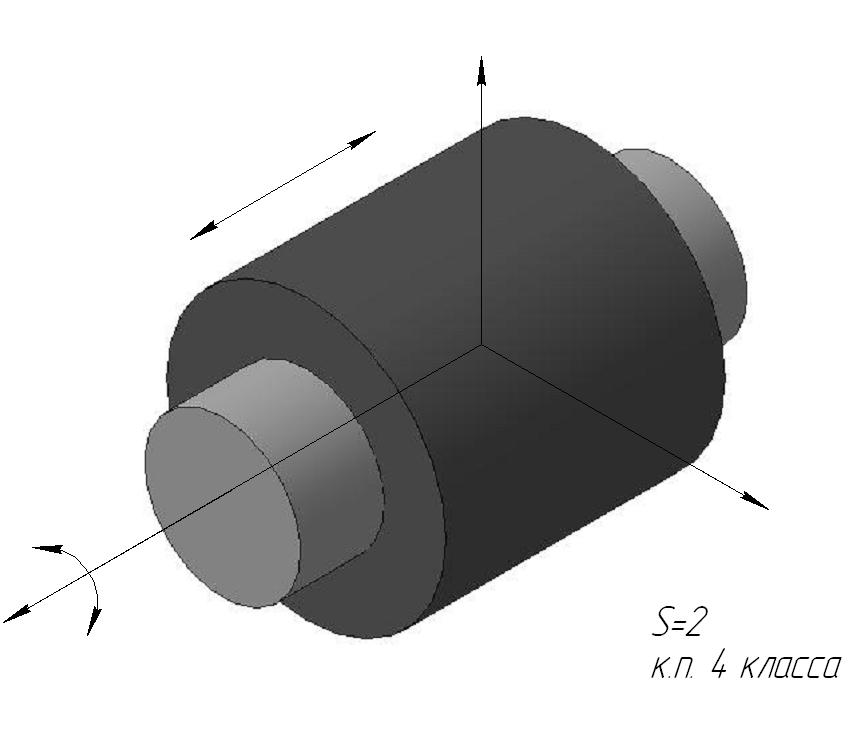
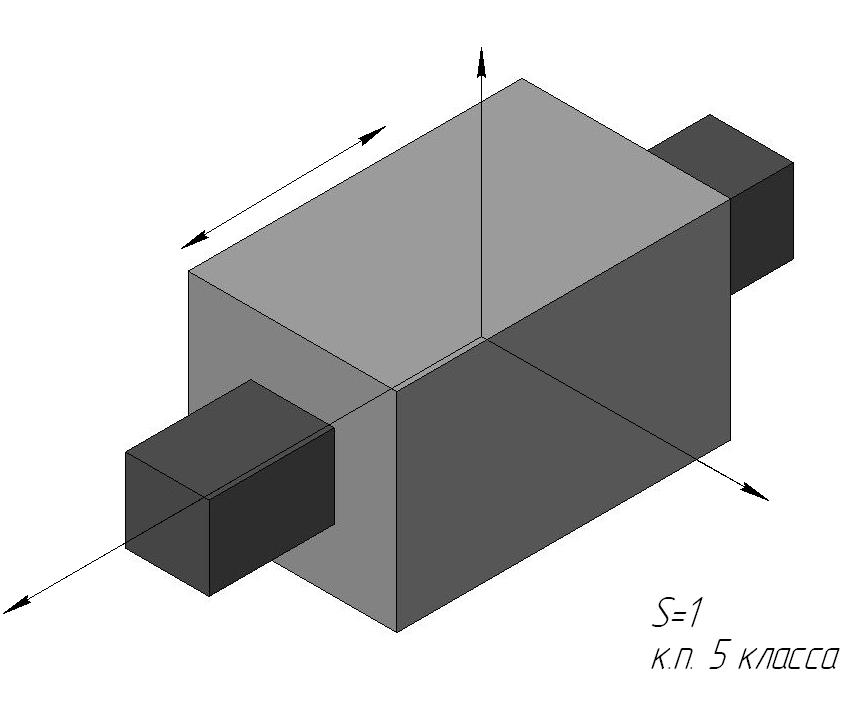
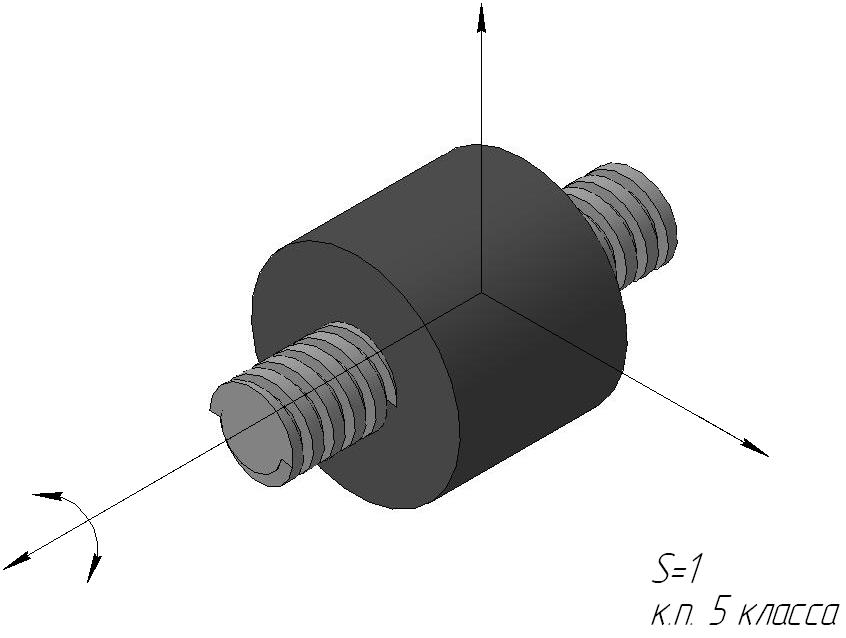
Двухподвижная кинематическая пара (пара четвертого класса) представлена цилиндрической парой. Возможным перемещением здесь соответствует поворот вокруг оси пальца. Наконец, одноподвижные кинематические пары (пары пятого класса) представлены в трех вариантах. В поступательной паре относительное движение ее звеньев прямолинейно-поступательное, во вращательной паре — вращательное и в винтовой паре — винтовое, т. е. движение, при котором перемещения вдоль и вокруг какой-либо оси связаны между собой определенной зависимостью.
4. Кинематическая схема м-ма. Степени свободы.
Число степеней свободы или подвижность механизма - число независимых обобщенных координат однозначно определяющее положение всех его звеньев на плоскости или в пространстве. Если в пространственной к. ц., состоящей из «n» подвижных звеньев, имеются к.п. 1-ого, 2-ого,… 5-ого класса, число которых, соответственно, p1,p2,… p5, то к. ц. имеет число степеней свободы, определяемое формулой А.П. Малышева.
W=6n-5p5-4p4-3p3-2p2-p1 (3.1)
Так как любой механизм имеет одно неподвижное звено (стойку) и «n» подвижных звеньев, то формула (3.1) может использоваться для определения W пространственного механизма, где n – число подвижных звеньев, а W – степень подвижности механизма, показывающая сколько нужно иметь ведущих звеньев (двигателей) для получения определенного движения остальных его звеньев.
Для плоского механизма степень подвижности определяется по формуле Чебышева:
W=3n-2p5-p4, (3.2)
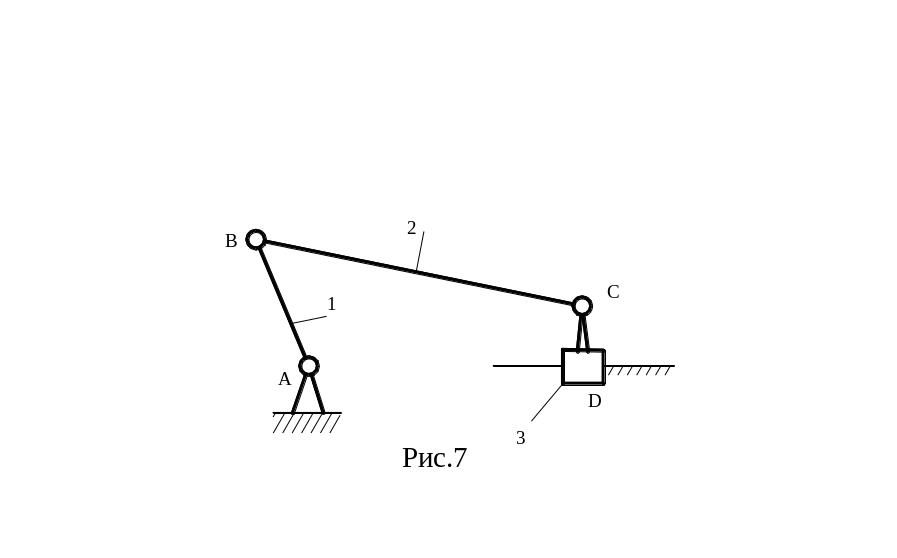
При этом к.п. 5-ого класса существует в виде поступательных, вращательных и винтовых.
Например, кривошипно-ползунный плоский меха-низм (рис.7), в котором n=3; p5=4; p4=0,
имеет W=3·3-2·4-0=1.
При определении W необходимо учитывать возможность наличия так называемых «пассивных» звеньев, т.е. звеньев, устраняемых без формального ущерба для кинематики анализируемого механизма .
а) W=3·4-2·6-0=0 – с пассивным звеном,
б) W=3·3-2·4-0=1 – фактически.
Кроме того, необходимо учитывать возможность наличия избыточных связей, которые не реализуются в реальном механизме, а их число q определяется разностью между числом связей в к.п. действительного и формально возможного механизмов.
На рис. 9, а показан действительный механизм, а на рис. 9, б – формально возможный механизм, имеющий функциональное назначение, аналогичное действительному механизму, но где все связи, в отличие от действительного механизма, реализованы.
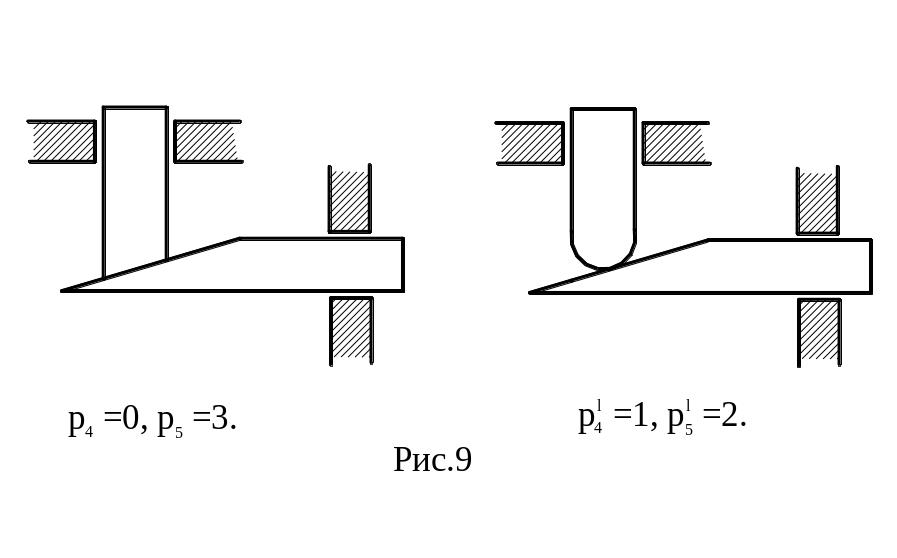
Число избыточных связей q в действительном механизме равно:
q=(2p5+p4)-(2p/5+p/4)=(2·3+0)-(2·2+1)=1,
т.е. степень подвижности действительного механизма равна:
W=3n-2p5-p4+q=3·2-2·3-0+1=1.
В общем случае пространственного механизма:
W=6n-i·pi+q, (i от 1 до 5).
5. Избыточные связи и подвижность.
6. Структурный синтез плоских механизмов. Группы Асура.
Основной принцип образования рычажных механизмов был сформулирован в 1914 году профессором Л. В. Ассуром и заключается в следующем.
Схема любого механизма может быть составлена последовательным присоединением к входным (начальным) звеньям и стойке к.ц. с нулевой степенью подвижности. Такие к. ц. называются структурными группами Ассура. Примеры различных групп Ассура показаны на рис.10.
Начальное звено со стойкой образует простейший механизм 1-ого класса (рис.11).
Путем присоединения к таким механизмам различных групп Ассура можно получить механизм любой сложности.
Группы Ассура классифицируются по числу к.п., которыми они присоединяются к основному механизму. Это число определяет порядок группы. Кроме того, группа Ассура имеет класс, определяемый числом к.п., образующих наиболее сложный замкнутый контур.
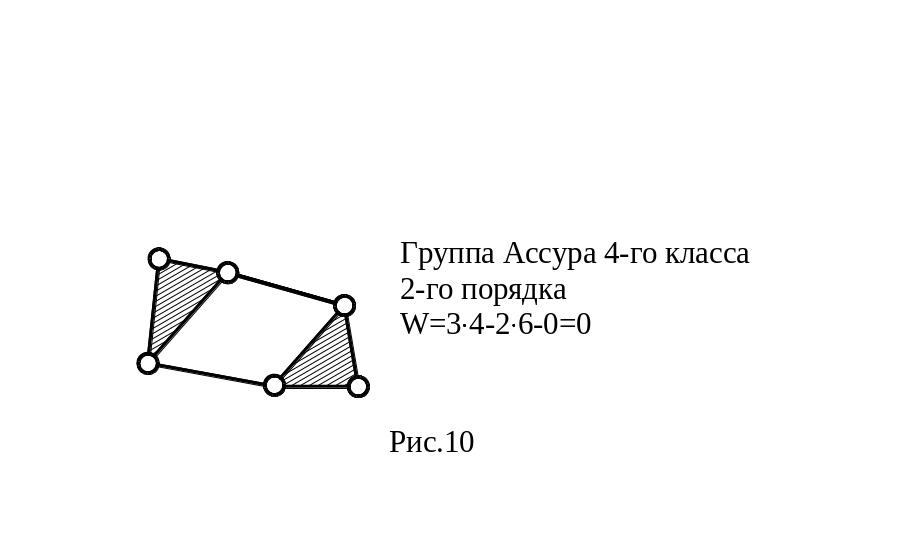
Состав и последовательность присоединения групп Ассура в механизме можно выразить его формулой строения. Механизм в целом классифицируется по группе наивысшего класса. На рис.12 показан пример такой классификации.
7. Классификация механизмов.
Основные виды механизмов.
Среди всего многообразия конструкций механизмов различают: стержневые (рычажные), кулачковые, фрикционные, зубчатые механизмы, механизмы с гибкими звеньями (например, ременные передачи), гидравлические, пневматические и др. виды.
Менее распространенные классификации подразумевают наличие механизмов с низшими или высшими парами в плоском или пространственном исполнении и т.д.
Учитывая возможность условного превращения практически любого механизма с высшими парами в рычажный, в дальнейшем наиболее подробно будем рассматриваеть именно эти механизмы.
Среди рычажных механизмов наиболее распространенны так называемые четырехзвенные, примеры которых представлены на рис.13, а-г.
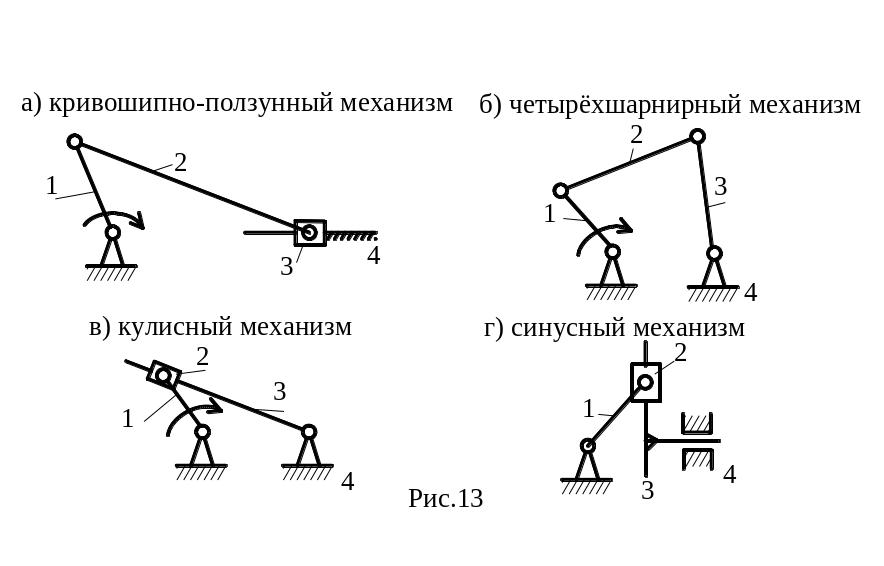
В этих механизмах встречаются однотипные звенья: кривошип – звено, совершающее полнооборотное вращательное движение вокруг неподвижной оси; коромысло – звено, совершающее неполнооборотное вращательное движение вокруг неподвижной оси; ползун – звено, совершающее поступательное движение относительно стойки; камень – звено, совершающее поступательное движение относительно подвижной направляющей, называемой кулисой; шатун – звено, совершающее плоскопараллельное движение.
Гидравлические и пневматические механизмы.
Гидравлическим называется механизм, в котором преобразование движения происходит посредством твердых и жидких тел. На рис.3 показана схема гидравлического механизма с применением условных обозначений по ГОСТ 2781—68 и 2782—68.
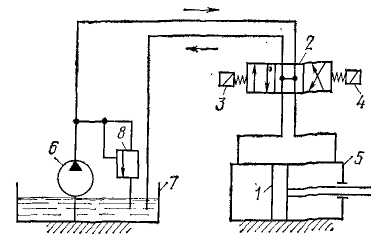
Механизм предназначен для привода в движение поршня 1 и потому называется гидроприводом. Поршень 1 движется направо или налево в зависимости от положения подвижного элемента распределителя 2. Этот элемент поочередно получает движение от электромагнитов 3 и 4. Если оба электромагнита выключены, то подвижный элемент распределителя 2 занимает среднее положение, показанное на схеме. В этом положении перекрыты обе линии, по которым жидкость может поступать в цилиндр 5. При включении электромагнита 3 его сердечник передвигает подвижный элемент распределителя вправо. Чтобы представить себе действие распределителя в новом положении, надо мысленно передвинуть на место исходной (средней) позиции квадрат, расположенный слева, оставляя линии связи на месте. Тогда правая полость цилиндра 5 соединяется с насосом 6, а левая — с баком 7 и поршень под действием давления жидкости перемещается влево. При включении электромагнита 4 подвижный элемент распределителя 2 перемещается влево, а поршень 1 — вправо. В схеме предусмотрен переливной клапан 8 для перелива жидкости в бак при повышении ее давления.
Схема пневматического механизма имеет аналогичный вид, только насос 6 заменяется источником сжатого воздуха, а вместо соединения с баком 7 выполняется соединение с атмосферой.
8. Проектирование кинематических схем плоских рычажных механизмов. Общие принципы и понятия.
Кинематический анализ механизмов включает вопросы изучения звеньев с геометрической точки зрения, т.е. без учета действующих сил. Для этого используются графические, аналитические и экспериментальные методы исследования.
Одним из наглядных методов является графоаналитический, который включает:
а) построение планов положения механизма; б) определение скоростей и ускорений характерных точек или звеньев механизма.
При графических построениях на чертеже изображаются длины звеньев, скорости, ускорения и др. величины в определенном масштабе, характеризуемом масштабным коэффициентом:
=значение параметра/длина отрезка.
Например, вектор pa длиной 10 мм изображает скорость V=20 м/с. Тогда v=20/10=2 м·с-1/мм.
4.1. Построение планов положения механизма
Графическое изображение взаимного расположения звеньев механизма, соответствующее заданному моменту времени, называется планом положений или планом механизма.
Рис. 14
Планы положения строятся в определенном масштабе методом засечек в соответствии с формулой строения механизма, При этом должны быть заданы линейные размеры всех звеньев (рис.14).
После построения нескольких совмещенных планов механизма при необходимости можно определить графически траектории характерных точек звеньев, имеющих сложное движение, например, центра тяжести S шатуна AB (рис.14).
4.2. Определение скоростей и ускорений механизма методом планов
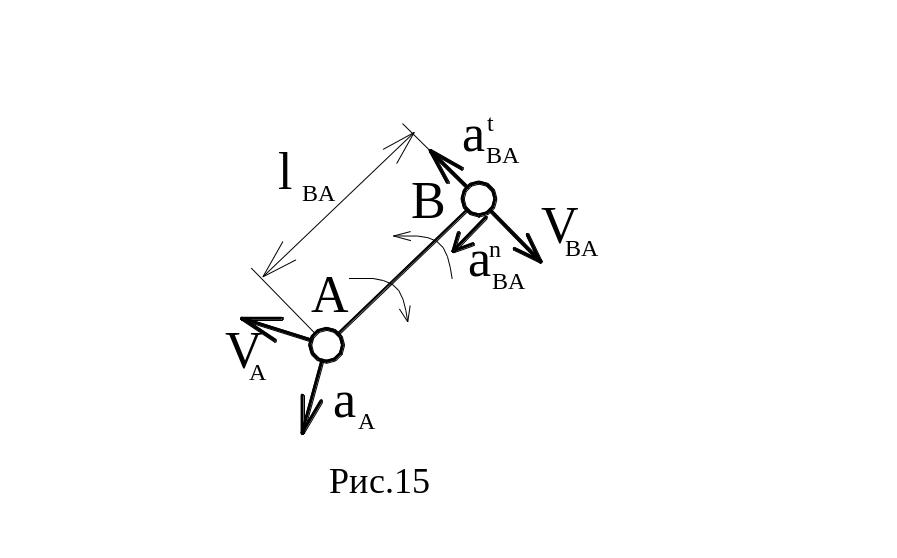
Метод планов является одним из самых наглядных. Определению подлежат линейные скорости и ускорения отдельных точек и угловые скорости и ускорения звеньев. При этом предварительно составляются векторные уравнения для скоростей и ускорений точек звеньев, совершающих сложное движение, например:
а)
звено совершает плоскопараллельное
движение, состоящее из переносного,
т.е. поступательного со скоростью полюса
и относительного вращательного вокруг
полюса (рис.15).
Принимая за полюс т. A, получим:
VB=VA+VBA;
где
VBA=·lAB;
aB=aA+aBA; где aBA=anBA+atBA при
anBA=2·lAB; atBA=·lAB.
Здесь V, a, , - линейные скорости и ускорения соответствующих характерных точек, а также угловые скорость и ускорение звена (индексы соответствуют характеру ускорений и обозначениям точек).
б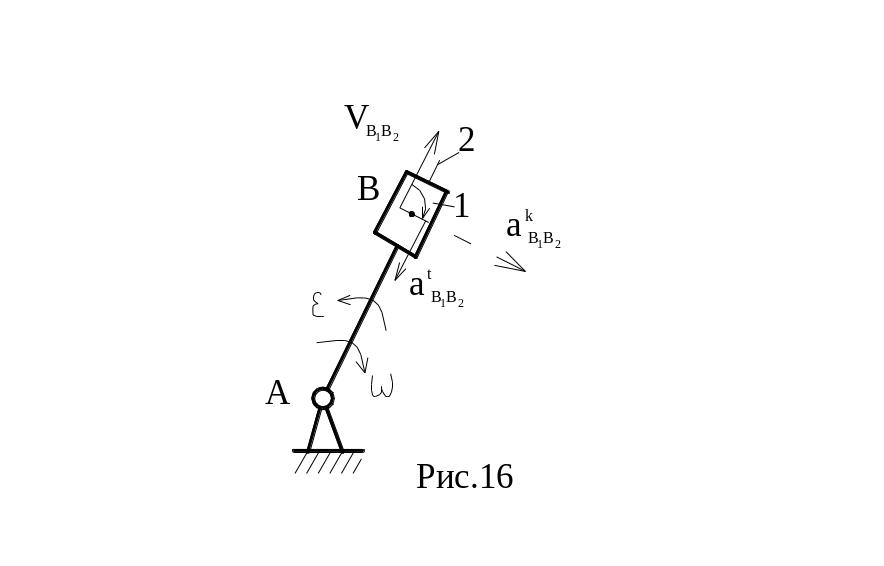
)
звено совершает сложное движение,
состоящее из переносного вращательного
и относительного поступательного,
например, звено 1 (рис.16).
Пусть B1 и B2 – точки, принадлежащие звеньям 1 и 2. Тогда:
VB1=VB2+VB1B2, где VB2=·lAB.
aB1=aB2+atB1B2+akB1B2, где ускорение Кориолиса
akB1B2=2VB1B2· и совпадает с направлением вектора VB1B2, повернутого на 90○ в сторону переносного вращения.
Решение векторных уравнений осуществляется графически путем построения так называемых планов скоростей и ускорений, на которых абсолютные скорости и ускорения откладываются от одной точки, называемой полюсом, в определенном масштабе.
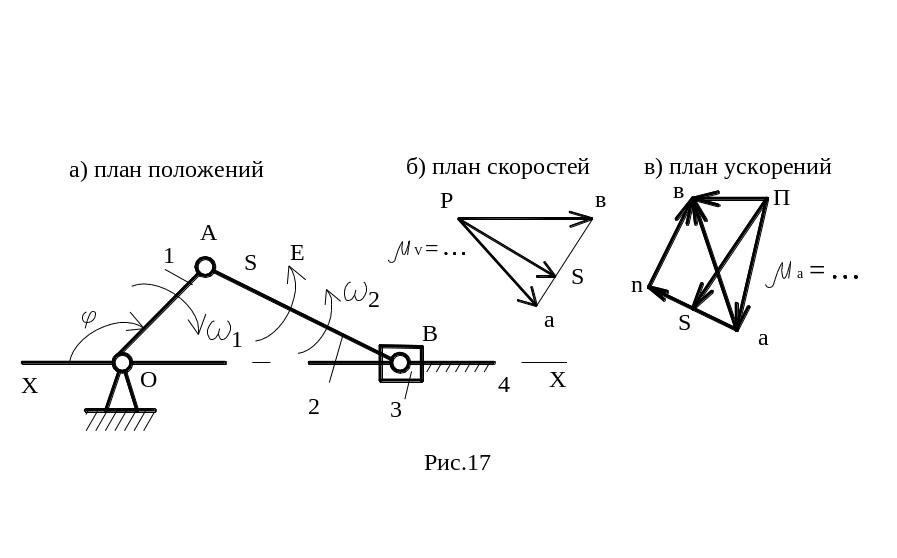
Пример расчета кривошипно-ползунного механизма рассмотрен на рис.17, где план положений (рис.17, а), план скоростей и ускорений (рис.17, б, в).
Векторные уравнения для скоростей записываются в виде:
VB=VA+VBA; VB=VBx+VBBx;
где VA=1·lOA; VBx=0; VBA_|_AB; VBBx||x-x,
т.е. в выбранном масштабе μV: pb||x-x; ab_|_AB
VBA= μV·ab; VB= μV·pb и 2= VBA/ lAB.
Векторные уравнения для ускорений при 1=const записываются в виде:
a B=aA+aBA; aB=aBx+akBBx+atBBx; где aA=anA=12·lOA; aBA=anBA+atBA;
здесь anBA=22·lAB; atBA=ε2·lAB; aBx=0; akBBx=0; atBBx||x-x.
Все ускорения представлены на рис.17 в выбранном масштабе μa в виде соответствующих отрезков, например, aB=μa·πb и т.д.
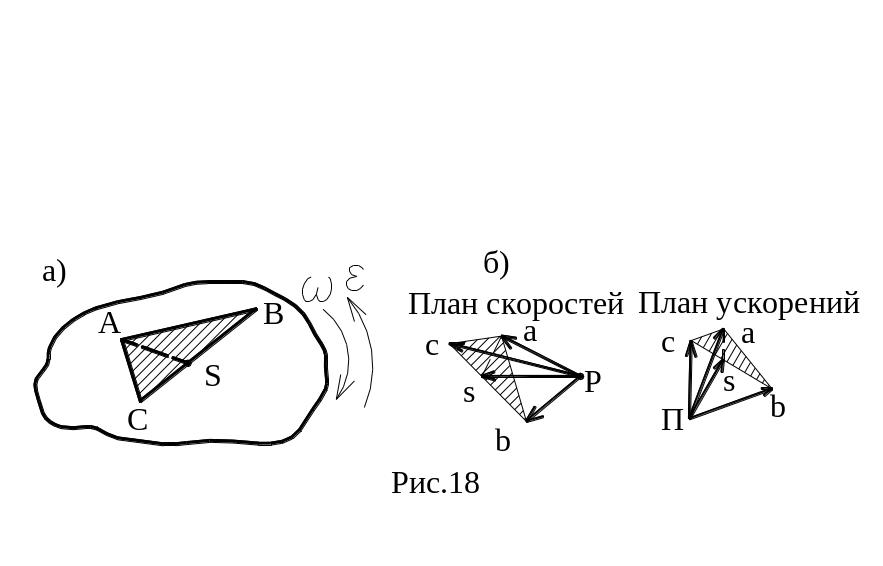
При определении скоростей и ускорений промежуточных точек звеньев, например т. S, можно использовать так называемую теорему подобия, согласно которой точки на плане положений звеньев и соответственные точки на планах скоростей и ускорений образуют подобные фигуры или пропорциональные отрезки. Рассмотрим доказательство данной теоремы. На рис.18 показано звено ABC и планы скоростей и ускорений для точек этого звена:
отрезок ca на плане скоростей соответствует VCA_|_CA;
отрезок ca на плане скоростей соответствует VCA_|_CA;
отрезок ab на плане скоростей соответствует VAB_|_AB;
отрезок bc на плане скоростей соответствует VBC_|_BC;
т.е. треугольник abc подобен треугольнику ABC.
Ускорения относительного (вращательного) движения равны:
;
;
,
т.е. aCA/ lCA =aAB/ lAB =aBC/ lBC или ca/CA=ab/AB=bc/BC,
Следовательно, треугольник abc подобен треугольнику ABC. Аналогичным является построение фигур для любой промежуточной точки, например т. S (рис.18, а, б).