Визначенням границі по Гейне

Нехай функція   визначена у всіх точках проміжку  , за винятком, можливо, деякої точки  . Побудуємо послідовність значень аргументу функції  :

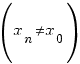,    , (1) таку, щоб всі члени послідовності належали проміжку   і послідовність збігалась до точки  :

. Тоді значення функції 

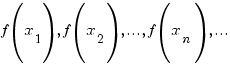. (2) також утворять деяку числову послідовність.

Говорять, що число   є границею функції   при  , що прямує до  , якщо для будь-якої послідовності значень аргументу (1), яка збігається до числа  , послідовність значень функції (2) збігається до числа  , і пишуть

___________________________________________________________________________________

Границя числової послідовності

Границя числової послідовності, число, до якого члени послідовності прямують зі збільшенням індекса в сенсі наступного означення:

Дійсне число a називається границею числової послідовності  , якщо  ^[1]

Позначення:   або 

При цьому також кажуть, що послідовність   збігається до числа a, або має границю a. Послідовність, що збігається до деякої границі називається збіжною, в інших випадках — розбіжною.

Числова́ послідо́вність  — послідовність  дійсних чисел, тобто відображення, яке кожному натуральному числу n ставить у відповідність дійсне число  . Число  називають елементом або членом послідовності.

Числовою послідовністю називається функція, визначена на множині натуральних чисел. Позначається числова послідовність звичайно через , де , – n-й член послідовності.

Наведемо приклади числових послідовностей.

Приклад 1. Нехай числова послідовність задана загальним членом 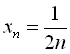. Це означає, що кожному натуральному числу n відповідає певний член послідовності . Надаючи n значення 1, 2, 3, …, дістанемо послідовність : …; … .

Приклад 2. Нехай послідовність задана формулою . Усі члени послідовності з непарними номерами дорівнюють , а з парними номерами дорівнюють 1: … . Дістаємо послідовність 1; 1; … .

Інтервали спадання функції.

Определение убывающей функции.

Функция y=f(x) убывает на интервале X, если для любых   и  выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.

________________________________________________________________________________________

Теорема спадання функції

Возрастание и убывание дифференцируемой функции связано со знаком её производной. Напомним,

что функция   называется возрастающей на интервале  , если для любых двух точек   из неравенства   следует, что  ; убывающей на интервале  , если из неравенства   следует, что  ; невозрастающей на интервале  , если из неравенства   следует, что  , и неубывающей на интервале  , если из неравенства   следует, что  .

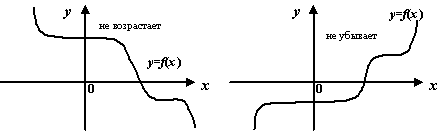
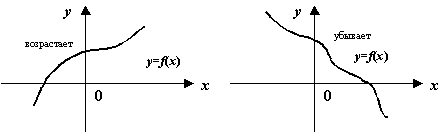
Рис.Графики возрастающей, убывающей, невозрастающей и неубывающей функций

Очевидно, что функция   возрастает тогда и только тогда, когда убывает функция  ; аналогичное утверждение связывает неубывающую функцию с невозрастающей.

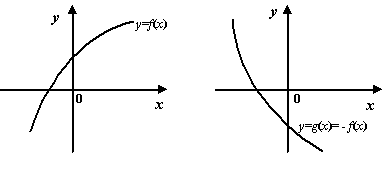
Рис.7.16.Графики функций   и 

Теорема 7.2   Пусть функция   дифференцируема на интервале   и   при всех  . Тогда   возрастает на  . Если же   при всех  , то   не убывает на  .

Аналогично, если   при всех  , то   убывает на  , а если   при всех  , то   не возрастает на  .

Доказательство.     В силу предыдущего замечания, теорему достаточно доказывать только для случаев   и  . Пусть   при всех   и  ,  . Применим к отрезку   формулу конечных приращений:

где  . В правой части   и  , так что  , откуда  , что означает возрастание функции.

Точно так же, если  , то получаем  , откуда  , что означает неубывание функции.