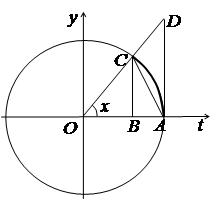Теорема Роля (Ролля)

Если функция   является непрерывной на отрезке [a, b] и дифференцируемой на интервале (a, b), принимает на концах этого интервала одинаковые значения (т.е.  ), то на этом интервале найдётся хотя бы одна точка x=c, в которой производная функции f(x)равна нулю, т.е.   

Теорема про суму границь

Границя суми дорівнює сумі границь,якщо останні існують.

 Доведення. Нехай, наприклад,  ,  . Покажемо, що  . Дійсно

;

  .

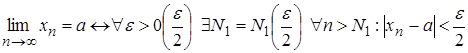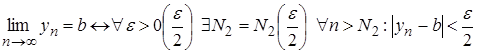 За   оберемо   та оцінимо модуль  , маємо:

Таким чином,

  ________________________________________________________________________________________

Асимптоти графіка функції

Пряма називається асимптотой графіка ф-ї якщо відстань від точки на графіку до прямої прямує до нуля у випадку,коли відстань від цієї точки до початку координат прямує до нескінченності.

Вертикальной асимптотой графика функции  называется вертикальная прямая   , если   или   при каком-либо из условий:   ,   ,   . Заметим, что мы при этом не требуем, чтобы точка   принадлежала области определения функции   , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:  или   , где   .  

 Наклонной асимптотой графика функции   при  называется прямая   , если выполнены два условия: 1) некоторый луч  целиком содержится в   ;

2) расстояние по вертикали между графиком и прямой стремится к 0 при   :   

1) Наклонной асимптотой графика функции   при   называется прямая   , если 1) некоторый луч   целиком содержится в   ; 2) расстояние по вертикали между графиком и прямой стремится к 0 при   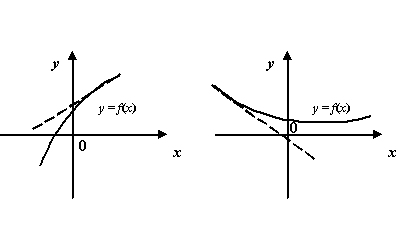:         Рис. 7 . 6 .Графики функций, имеющие наклонные асимптоты при   и при   В случае, если наклонная асимптота расположена горизонтально, то есть при   , она называется горизонтальной асимптотой . Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая   является горизонтальной асимптотой графика  при   или   , если   или   соответственно. 

Эквивалентные бесконечно малые, применение к нахождению пределов.

Функции   и   называют бесконечно малыми при  , если   и 

Функции   и   называют эквивалентными бесконечно малыми при  , если 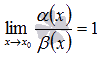 Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.

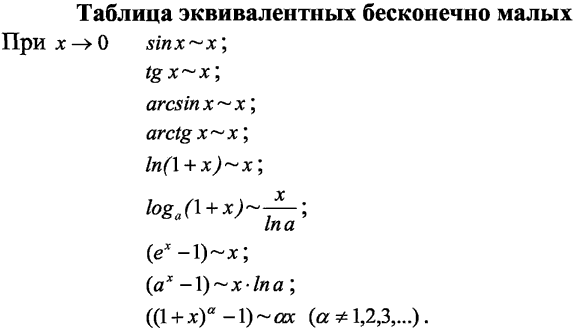Эквивалентность всех величин таблицы можно доказать, основываясь на равенстве 

_______________________________________________________________________________________

Предельный переход в неравенствах

Теорема. Если элементы сходящейся последовательности {x_n}, начиная с некоторого номера, удовлетворяют неравенству x_n ≥ b (x_n ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).

 Доказательство. Пусть все элементы x_n, по крайней мере начиная с некоторого номера, удовлетворяют неравенству x_n ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {x_n}, то для положительного ε = b - a можно указать номер N такой, что при n ≥ N выполняется неравенство |x_n - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < x_n - a < b -a. Используя правое из этих неравенств, получим x_n < b, а это противоречит условию теоремы. Случай x_n ≤ b рассматривается аналогично. Теорема доказана.

Формула Тейлора

        

        

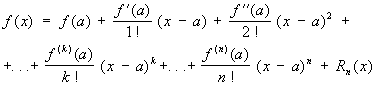
        изображающая функцию f (x), имеющую n-ю производную f ⁽ⁿ⁾(a) в точке х = а, в виде суммы многочлена степени n, расположенного по степеням х—а, и остаточного члена R_n (x), являющегося в окрестности точки а бесконечно малой более высокого порядка, чем (x—a) ⁿ [то есть R_n (x) = an (x)(x—a) ⁿ, где an (x) → 0 при х → а]. Если в интервале между а и х существует (n + 1)-я производная, то R_n (x) можно представить в видах:  

        ,

        где ξ и ξ₁ — какие-то точки указанного интервала

_______________________________________________________________________________________

Теоре́ма Лагра́нжа ( доведення )

Якщо функція   неперервна на проміжку  , диференційована в  , то знайдеться принаймні одна точка   така, що має місце формула.:

Доведення

Розглянемо на проміжку   наступну допоміжну функцію:

Перевіримо, що для функції   виконані всі умови теореми Ролля. І справді,   неперервна на проміжку   (як різниця функції   та лінійної функції) та в усіх внутрішніх точках проміжка   має похідну:

З формули (1) очевидно, що  .

Згідно з теоремою Ролля на проміжку   знайдеться точка   така, що

З рівності (2) витікає формула Лагранжа. Слід відзначити, що не обов'язково вважати  .

Зауваження

У цьому випадку формулу Лагранжа отримано як наслідок з теореми Ролля. Проте, теорема Ролля сама є частковим випадком теореми Лагранжа.

Послідовність. Границі послідовності з доведенням

______________________________________________________________________________________

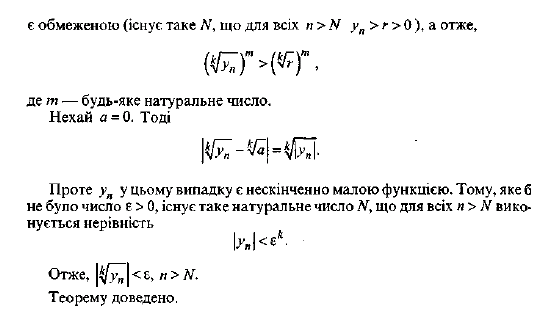Інтегрування частинами

Для невизначеного інтеграла

Функції   и   повні, отже, можливе диференціювання:

Ці функції також неперервні, значить можна взяти інтеграл від обох частин рівності:

Операція інтегрування протилежна диференціюванню:

Після перестановок:

Для визначеного

У цілому аналогічно випадку для невизначеного інтеграла:

______________________________________________________________________________________

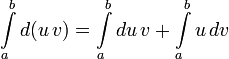
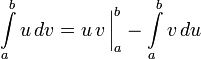
Неперервність функції

Функція   дійсної змінної, яка означена в області  , неперервна в точці   якщо для довільного   знайдеться таке   (яке залежить від  ), що з   випливає   Функція   неперервна в області  , якщо   неперервна в кожній точці цієї області.

Нехай  ,   — гранична точка множини A.

Теорема акатора:якщо функція неперервна на відрізку,то вона буде рівномірно неперервною на цьому відрізку.

Зауваження: якщо функція неперервна на інтервалі,то вона може бути не рівномірно неперервною на цьому інтервалі.

Свойства непрерывных функций. Непрерывность сложной функции

Теорема 1. Пусть функции f(x) и g(x) непрерывны в точке х₀. Тогда функция f(x) не равная g(x), f(x)g(x) и   (если g(x) не равно 0) непрерывны в точке x0.

Доказательство.

Пусть f(x) и g(x) непрерывны в точке x₀. Это значит, что  . Но тогда, по свойствам пределов

Последнее свойство верно, если  . 

Теореми про монотонність функції

Определение 1: Функции   называется возрастающей [убывающей] на множестве  , если для любых значений аргумента   из   выполняется условие    .

Определение 2: Промежутки области определения, на которых функция возрастает или убывает, называются промежутками монотонности функции.

Определение 3: Функция   называется возрастающей [убывающей], если для любых значений аргумента   из   выполняется условие    .

Определение 4: Возрастающие и убывающие функции называются монотонными.

Теорема 1. Если функция   возрастает на множестве  , а функция  убывает на множестве  , то уравнение   имеет на   не более одного корня.

Теорема 2. Если функция   монотонна на множестве  , а функция  постоянна на множестве  , то уравнение   имеет на   не более одного корня.

______________________________________________________________________________________

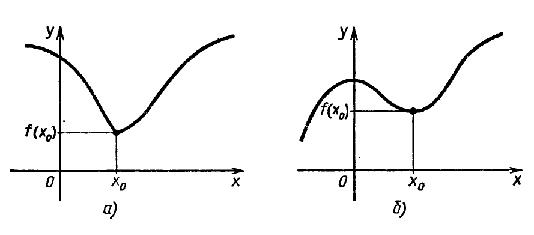
Необхідна умова існування мінімуму функції з доведенням.

Точка x0 называется точкой минимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≥ f(x0.  Это наглядно показано на рисунке 1:   

Умовний екстремум

Нехай   - відкрита множина і на G задані функції  . Позначимо через   таку, що

 - рівняння зв’язку.

Визначення

Нехай на G визначена функція  . Точка   називається точкою умовного екстремуму функції   відносно рівнянь зв'язку, якщо вона є точкою звичайного екстремуму   на множині E ( розглядаються околи   ).

Формулой Маклорена называется формула Тейлора при а = 0:

Перша важлива границя

Розглянемо функцію  . Значення цієї функції при   не існує, але  .

Теорема. Справедлива рівність

 

Границю      називають першою важливою (першою чудовою) границею.

Доведення. Нехай   (x вимірюється в радіанах).

 

Рис. 2.3

Розглянемо рис. 2.3, на якому позначено  ,  ,  ,  . Виходячи з геометричних міркувань матимемо:   ; ;   .

Оскільки  , то, поділивши останню нерівність на  , матимемо:

 або  .

 

Знайдемо  ,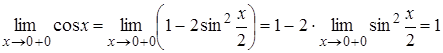

.

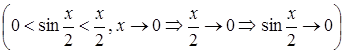Отже,  . У випадку   доведення проводиться аналогічно. Тут маємо:

. Об’єднаємо отримані результати:

 

. Графік функції   має вигляд .

______________________________________________________________________________________

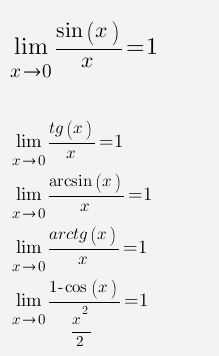Производная показательной и логарифмической функции

Предполагается, что основание a показательной функции больше нуля и не равно единице: a > 0, a ≠ 1. Производная показательной функции y = ax с основанием a определяется формулой где ln a - натуральный логарифм a, т.е. логарифм a по основанию е, приблизительно равному 2,718281828... ( Если a = е, то получаем красивый результат в виде

Производная показательной функции.

• Вывод формулы производной приведем на основе определения:

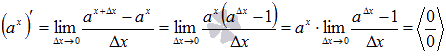
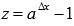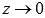• Пришли к неопределенности. Для ее раскрытия введем новую переменную , причем при . Тогда 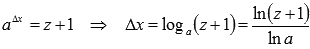. В последнем переходе мы использовали формулу перехода к новому основанию логарифма.

• Выполним подстановку в исходный предел:

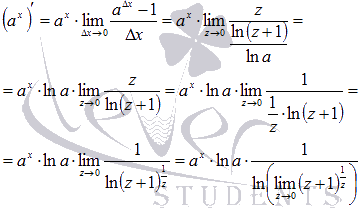
• Если вспомнить второй замечательный предел, то придем к формуле производной показательной функции:

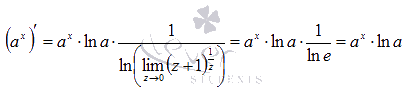
Універсальна тригонометрична підстановка 

Теорема. Інтеграл виду   за допомогою підстановки   перетвориться в інтеграл від раціонального дробу.  Для доказу висловимо   ,   і   через   : 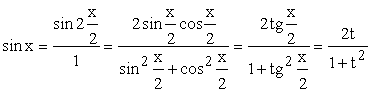  ; 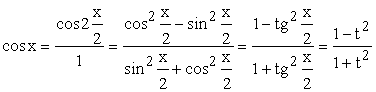  ;   .  У результаті проведених перетворень   ,   і   перетворилися на раціональні дробу від   . Підставляючи їх у вихідний інтеграл, отримуємо: 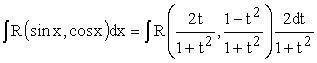  .  У даному виразі раціональні дроби підставлені в раціональну функцію. Так як над ними виконуються лише арифметичні операції, то в результаті виходить також раціональний дріб. Отже, раціональну функцію від тригонометричних функцій можна проінтегрувати, перетворивши її в раціональну дріб.  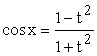Підстановка   ,   ,   ,  називається універсальної тригонометричної підстановкою. ______________________________________________________________________________________