Завдання
Визначити тип вхідного потоку. Провести перевірку статистичної гіпотези про тип вхідного потоку з використанням критерію Пірсона.
Хід роботи
Використовуючи схему моделювання вхідного потоку з Лаб. 1, отримати статистичний ряд інтервалів часу між надходженнями сусідніх вимог (закон розподілу задається викладачем).
Для автоматизації подальших розрахунків створити новий файл в середовищі Matlab (File/New/M-File).
Перехідний процес.
Побудувати варіаційний ряд, тобто відсортувати дані, що знаходяться в робочій області, в порядку зростання (функція Matlab sort(х)).
Сформувати вектор, що буде включати лише ненульові значення інтервалів часу. Наприклад, для відсортованого вектора delta_t у якого перші 3 значення дорівнюють 0, необхідно записати delta_t:= delta_t(4:size(delta_t);1)
Визначити розмір вибірки: n=size(delta_t).
Знайти максимальний та мінімальний елементи вибірки (функції Matlab max(delta_t), min(delta_t)). Розрахувати розмах варіації
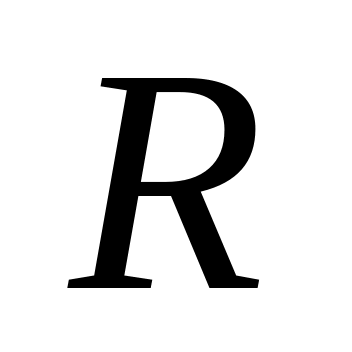.Обчислити величину інтервалу варіаційного ряду
та кількість інтервалів
,
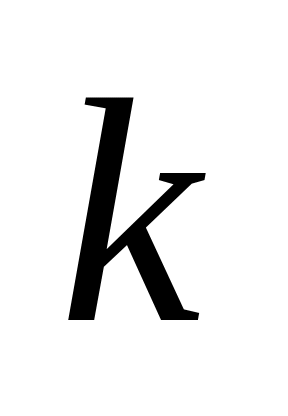яка має бути цілим числом. Для округлення
результату розрахунків можна використати
функцію round(f)).Підрахувати кількість значень, що потрапили в кожен з інтервалів
та обрахувати частоту
.
Дані занести в табл. 3.
Таблиця 3
Інтервал |
|
|
... |
|
... |
|
Кількість спостережень |
|
|
... |
|
... |
|
Частота |
|
|
... |
|
... |
|
Теоретична імовірність |
|
|
... |
|
|
|
Теоретична
кількість спост. |
|
|
… |
|
… |
|
Розрахувати статистичні числові характеристики випадкової величини: математичне очікування mean(х), дисперсію, середньоквадратичне відхилення std(х).
Побудувати полігон, гістограму та статистичну функцію розподілу. Базуючись на отриманих графіках, висунути гіпотезу про теоретичний закон розподілу випадкової величини.
Визначити теоретичну імовірність потрапляння випадкової величини в заданий інтервал
та теоретичну кількість спостережень
.
Дані занести в табл. 3.Побудувати графік теоретичного розподілу, сполучивши його з гістограмою статистичного розподілу.
Обрахувати значення міри розходження
.
Визначити число ступенів свободи
та імовірність розходження.Оформити звіт з лабораторної роботи, який повинен містити програму Matlab для розрахунків з коментарями та результатами виконання, заповнену табл.3, побудовані вручну графіки, розрахунки та висновки що до результатів перевірки гіпотези.
Контрольні питання
Які характеристики лежать в основі класифікації випадкових величин?
Дати визначення поняттям стаціонарність, ординарність та відсутність післядії.
Які характеристики повинен мати потік для того, щоб його можна було віднести до потоків Пуассона?
В чому особливості нестаціонарного потоку Пуассона та неординарного потоку Пуассона.
Пояснити в чому різниця між статистичним рядом та варіаційним рядом.
Опишіть порядок визначення теоретичного закону розподілу випадкової величини.