- •Условно и абсолютно сходящиеся ряды. Перестановочное св-во абсолютно сходящихся рядовъ
- •Неравенство Абеля
- •Признак Вейерштрасса равномерной сходимости функционального ряда.
- •Теорема о почленном интегрировании функциональной последовательности
- •Ядро Дирихле
- •Регулярные функции. Достаточное условие сходимости ряда Фурье в точке.
- •Достаточное условие равномерной сходимости ряда Фурье
- •1.Определение двойного интеграла. Критерий интегрируемости. Интегрируемость непрерывных в ограниченной замкнутой области функций.
- •4. Сведение двойного интеграла к повторному. Общий случай
- •5. Определение тройного интеграла. Формулы замены переменных и повторного интегрирования для тройного интеграла.
4. Сведение двойного интеграла к повторному. Общий случай
Теор:
G ограниченная
замкнутая область. Проекция G
на Ox – [ab]
 Oy и пересекает
[a,b].
l
Oy и пересекает
[a,b].
l G промежуток[yH(x),yb(x)]
G промежуток[yH(x),yb(x)]


 сходится
сходится

Доказательство
R=
F(x,y):={ }
}
 ;
*()=F(x,y)
;
*()=F(x,y)
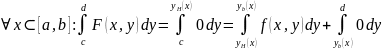
( ;
;

Замечание 1
[c,d]
проекция G на Oy.
Если
 G пересекается с
y=y0
по промежутку [xn(y0),xt(y0)]
и
G пересекается с
y=y0
по промежутку [xn(y0),xt(y0)]
и
 ,
то
,
то

5. Определение тройного интеграла. Формулы замены переменных и повторного интегрирования для тройного интеграла.
Кубируемые
области. Элементарные области: конечное
объединение прямоугольных параллелепипедов
с ребрами, параллельными осям координат
без общих внутренних точек.

 -
верхний объем G
-
верхний объем G
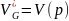 ;
P-элементарно;
;
P-элементарно;

V*G – нижний объем G
V*G=supV(p);
P –элементарно,
P G
G
G кубируемо если = V*G
Определение тройного интеграла
G- кубируемая область. f(x,y,z) в G
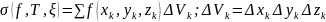

Переход к повторному интегралу
Теор:
 Проекция G на xOy
Gz.
Любая прямая пересекающая Gz
пересекает G по
промежутку [(xy,zH(xy),(xy,zb(xy))].
Если f(x,y,z)
интегрируема в G
и
Проекция G на xOy
Gz.
Любая прямая пересекающая Gz
пересекает G по
промежутку [(xy,zH(xy),(xy,zb(xy))].
Если f(x,y,z)
интегрируема в G
и

[s,t]
проекция G на Oz.


Замена переменных
G кубируема в (x,y,z).
G* в (uvw)
F:{x=x(uvw);y=y(uvw);z=z(uvw)}.
Условия на F: 1)
взаимная однозначность 2) C’(G*)
3)Якобиан 0
0

D* внутри G*, F(D*)=D внутри G
Теор.
Если f(x,y,z)
интегрируема в D,
то

6.Формулы замены в двойном и тройном интеграле. Полярные, цилиндрические и сферические координаты.
Теор. D*, G*, F, D, G квадрируемые области. f(x,y) интегрируема в D.

z

 Стандартные
замены
Стандартные
замены
Цилиндрическая





z

r
y
x


Сферическая


r
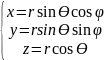 ;
;






y
x

7. Определение криволинейного интеграла первого рода. Свойства
 -естественная
параметризация
-естественная
параметризация
Г-
Г+


 криволинейные интегралы первого рода
от F
по Г и *(
криволинейные интегралы первого рода
от F
по Г и *( ;
*()=
;
*()=
Г-: ,
,


0=s0<s1<…<sn=S
длина

 tj),y(tj),z(tj))(sj-sj-1)
tj),y(tj),z(tj))(sj-sj-1)
8.Криволинейные интегралы второго рода. Свойства
Г гладкая(кусочно гладкая)
a( )=(P(xyz),Q(xyz),R(xyz))
)=(P(xyz),Q(xyz),R(xyz))


Опр.
 ;
;
 :=
(s)ds
:=
(s)ds
Если
 кусочно гладкая, то
кусочно гладкая, то
 ;
;

 -циркуляция
-циркуляция

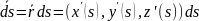

 P:
0=s0<s1<…<sn=S
;
P:
0=s0<s1<…<sn=S
;
 [sj-1,sj]
[sj-1,sj]


выбираем

 ,
так чтобы
,
так чтобы
 (
( )
)





(x(0),y(0),z(0))=()
9.Формула Грина. Случай элементарной области.
d C c
A B
a b
 ,
G односвязна в D.
D(xy), Q(xy),
dP/dy, dQ/dx
непрерывны. dG кусочно
гладкая. Тогда
,
G односвязна в D.
D(xy), Q(xy),
dP/dy, dQ/dx
непрерывны. dG кусочно
гладкая. Тогда



Доказательство при дополнительных ограничениях на G
 а)
G криволинейный
треугольник
а)
G криволинейный
треугольник
AB||Ox,
AC||Oy,
AC-график непрерывной
строго возрастающей функции y= ,x
,x
=-
=0,
т.к. x


 b
на [BC]
b
на [BC]
AC- график непрерывной строго возр. ф-ии


10.Формула Грина. Общий случай
G односвязная
Можно разбить на конечное число областей, для которых доказана формула Грина.
P,Q, dP/dy,
dQ/dx



 =
=
G-первоначал, G+ с разрезами
=
Следствие
Площадь G=
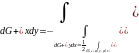
11. Условия независимости криволинейного интеграла второго рода от пути интегрирования
12 Условия независимости криволинейного интеграла второго рода от пути интегрирования для односвязной области
Пусть в области D заданы непрерывные функции P(x,y) и Q(x,y) и M0M – гладкая дуга, лежащая в области D.
Рассмотрим
вопрос о независимости интеграла
 от формы пути интегрирования. Место
имеет следующая теорема:
от формы пути интегрирования. Место
имеет следующая теорема:
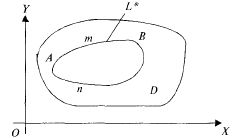
Теор . Пусть функции P,Q,P’Y,Q’X определены и непрерывны в односвязной ограниченной замкнутой области D в плоскости Oxy. Тогда следующие четыре условия равносильны между собой:
 ,
где L-
замкнутый контур в области D;
,
где L-
замкнутый контур в области D;
Интеграл не зависит от формы пути интегрирования, а зависит лишь от положения точек M0 и M.
Pdx+Qdy=dU- полный дифференциал некоторой функции U(x,y)
dQ/dx=dP/dy в каждой точке области D
1=>2


2=>3
Пусть
A(x0,y0),
 является функцией от x,y,
т.е.
является функцией от x,y,
т.е.
u(x,y)
= .
Чтобы
показать дифференцируемость u(x,y)
т.е. du=Pdx+Qdy,
достаточно доказать для
.
Чтобы
показать дифференцируемость u(x,y)
т.е. du=Pdx+Qdy,
достаточно доказать для
 По определению частной производной:
По определению частной производной:
 ,
где т.С(
,
где т.С( можно взять прямолинейным y=const.
Тогда
можно взять прямолинейным y=const.
Тогда

И по теореме о среднем для определенного интеграла получаем

Аналогично доказывается равенство du/dy
3=>4
Из условия 3 следует, что по теореме о
равенстве частных производных высших
порядков, отличающихся порядком
дифференцирования,

4=>1
Пусть
гладкая замкнутая кривая L*D
ограничивает
область

Тогда по формуле Грина

13.Касательная плоскость и нормаль к явно заданной поверхности. Достаточное условие существования невертикальной касательной плоскости
Если поверхность задана явно: z = f(x; у), то в точке X0(x0; y0; z0) она обладает касательной плоскостью
![]()
и нормалью
![]()
14. Понятие гладкой поверхности
Задание поверхности уравнением z=f(x,y)) (1) or x=f(y,z) (2) or y=f(x,z) (3)называется явным
Задание поверхности уравнением z=f(x,y,z) называется неявным
 -параметрическое
задание
-параметрическое
задание
Опр.
Пусть поверхность Ф задана явно, либо неявно, либо параметрически. Будем называть поверхность Ф гладкой, если для любой ее точки существует такая окрестность, которая вырезает часть поверхности Ф, допускающую явное представление любого вида(1,2,3), где f- непрерывно дифференцируемая функция
Если поверхность Ф задана явно уравнением (1) и функция f(x, y) непрерывно
дифференцируема в области G, то поверхность, очевидно, является гладкой.
Пусть поверхность Ф задана неявно уравнением (1) и пусть функция F(x, y, z) непрерывно дифференцируема. Точка М0(x0, y0, z0) поверхности Ф называется неособой, если в этой точке Fx2 + Fy2 + Fz2 ≠ 0. В противном случае точка называется особой. Если поверхность не содержит особых точек, то она является гладкой.
15. Касательная плоскость и нормаль к поверхности, заданной параметрически
Пусть поверхность Ф задана параметрически уравнениями (x = ϕ(u, v), y = ψ(u, v), z = χ(u, v), (u, v) ∈ g,), или, что то же самое,
уравнением (r = ϕ(u, v) i + ψ(u, v) j + χ(u, v) k, (u, v) ∈ g,). Точка M0(ϕ(u, v), ψ(u, v), χ(u, v)) называется неособой точкой поверхности Ф, если в этой точке векторы
ru = i ϕu(u, v) + j ψu(u, v) + k χu(u, v),
rv = i ϕv(u, v) + j ψv(u, v) + k χv(u, v), неколлинеарны (линейно независимы). В противном случае точка M0 называется особой. Простая поверхность, не имеющая особых точек, является гладкой.
Уравнение касательной плоскости к поверхности Ф в неособой внутренней точке M(ϕ(u,v), ψ(u, v), χ(u, v)) имеет вид A(x − x0) + B(y − y0) + B(М0)(z − z0) = 0.
где x0 = ϕ(u, v), y0 = ψ(u, v), z0 = χ(u, v),

Вектор N = [ru · rv] = i A + j B + k. С есть вектор нормали к поверхности Ф в точке M.
Векторы ru и rv, отложенные от точки M, лежат в касательной плоскости (рис).

16. Определение площади поверхностей, заданных в явном виде и параметрически

17