Розв’язання

Дано:

1. Природне світло, падаючи на грань ніколя, внаслідок подвійного променезаломлення розщеплюється на два рівноправні за інтенсивністю промені: звичайний (о) і незвичайний (е). Площина коливань для незвичайного променя лежить у площині рисунка (площина головного перерізу). Площина коливань для звичайного променя перпендикулярна до площини рисунка. Звичайний промінь (о) внаслідок повного внутрішнього відбивання від межі АB відбивається на затемнену поверхню призми і гаситься нею. Незвичайний промінь (е) проходить , крізь призму, зменшуючи свою інтенсивність на 5% внаслідок поглинання в товщі призми. Тому

,

де – інтенсивність природного променя, – інтенсивність променя, який пройшов через перший ніколь N₁ (поляризатор). Тоді

.

2. Плоскополяризований промінь інтенсивністю падає на другий ніколь N₂ (аналізатор) і також розщеплюється на звичайний і незвичайний. Звичайний промінь повністю поглинається призмою, а інтенсивність незвичайного променя , котрий виходить із ніколя N₂, визначається законом Малюса (без урахування поглинання світла в N₂)

,

де  – кут між площинами коливань у променях з інтенсивностями та .

Враховуючи втрати інтенсивності внаслідок поглинання в N₂, одержимо

.

Тоді

.

Підставляючи числові значення, одержимо:

;

.

Відповідь: ; .

Приклад 6. Трубка довжиною з водним розчином цукру розміщена між паралельними ніколями. Для одержання повного затемнення поля зору аналізатора довелось повернути його на кут 60°. Дослід проводиться з жовтим світлом, для якого питома постійна обертання . Визначити концентрацію цукру в розчині.

Розв’язання

Дано:

Спочатку пропускні напрямки поляризатора і аналізатора співпадали і поле зору аналізатора було максимально світлим. Розчин цукру повернув площину поляризації на кут  і поле зору стало темнішим. Для повного затемнення довелось аналізатор повернути ще на кут . Це згідно закону Малюса може бути при умові

.

Отже, кут повороту площини поляризації розчином

.

З другого боку,

.

Звідси

.

Підставляючи числові значення, в СІ одержимо:

.

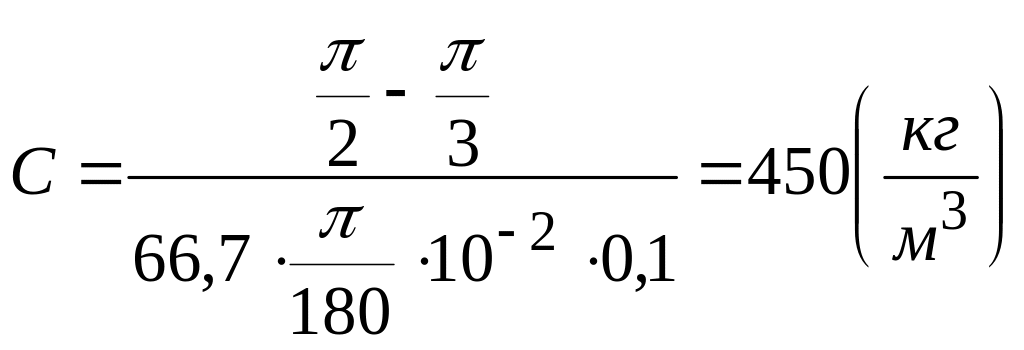Відповідь: 450кг/м³.

Приклад 7. Температура вольфрамової спіралі в 25-ватній електричній лампочці дорівнює 3000К. Відношення її енергетичної світності до енергетичної світності абсолютно чорного тіла рівна 0,3, Визначити площу випромінювальної поверхні спіралі. Вважати, що вся споживана потужність йде на випромінювання.

Розв’язання

Дано:

За визначенням енергетичної світності

. (1)

За законом Стефана-Больцмана

. (2)

Розділивши (1) на (2), з урахуванням даних задачі, отримаємо

.

Звідси випливає

. (3)

Підставимо числові дані у (3) і знайдемо шукану площу:

.

Відповідь: 1,810^-5 м².

Приклад 8. Кулька радіусом 1см з металу, робота виходу в котрого 2еВ, опромінюється світлом з довжиною хвилі . Визначити заряд кульки, якщо всі електрони віддаляються від її поверхні не більше ніж на 2см.