1.4 Сравнительная оценка результатов расчетов токов в ветвях различными методами

Результаты расчетов токов в ветвях заданной схемы представлены в таблице 1.

Таблица 1 – Результаты расчетов токов в ветвях цепи различными методами

Методы вычислений токов в ветвях цепи, А	Метод узловых и контурных уравнений	Метод контурных токов	Метод наложения
			частные токи (Е1=0)	частные токи (Е2=0)	сумма частных токов
I1	0,3931	0,3931	-0,0864	0,4796	0,3932
I2	0,0608	0,0608	0,2337	-0,1729	0,0608
I3	0,4539	0,4539	0,1472	0,3067	0,4539
I4	-0,3079	-0,3079	0,0306	-0,3385	-0,3079
I5	0,0852	0,0852	-0,0558	0,141	0,0852
I6	0,146	0,146	0,1779	-0,0319	0,146

Анализ полученных результатов показывает полное совпадение значений токов в ветвях при расчете их различными методами (согласно пунктов 1.1, 1.2 и 1.3).

1.5 Расчет баланса мощностей для заданной электрической цепи

Источники ЭДС Е₁ и Е₂ вырабатывают электрическую энергию, так как направление ЭДС и тока в ветвях с источниками совпадают. Баланс мощностей для заданной цепи рассчитаем с помощью следующего выражения

Е₁∙I₁ + Е₂∙I₂ = I₁²∙(R₁+r₀₁) + I₂²∙(R₂+r₀₂) + I₃²∙R₃ + I₄²∙R₄ + I₅²∙R₅ + I₆²∙R₆.

Подставляем в полученное выражение числовые значения и вычисляем

40∙0,3931+20∙0,0608 = (0,3931)²∙(45+1)+(0,0608)²∙(53+1) + (0,4539)²∙32 +

+ (─ 0,3079)²∙24 + (0,0852)²∙61 + (0,146)²∙15.

16,94 Вт = 16,94 Вт.

Из полученного равенства очевидно, что баланс мощностей выполняется.

1.6 Построение потенциальной диаграммы

Для построения потенциальной диаграммы выбирается замкнутый контур, включающий не менее двух источников ЭДС. Таким образом, возьмем контур БВИКАБ в соответствии с рисунком 6.

Рисунок 6 – Схема электрической цепи к расчету потенциалов в точках контура, содержащего две ЭДС

Зададимся направлением обхода контура против часовой стрелки. Заземлим одну из точек контура, пусть это будет точка Б. Потенциал этой точки равен нулю: φ_Б = 0 В.

Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки Б.

φ_В = φ_Б + I₅∙R₅ = 0 + 0,0852∙61 = 5,2 В,

φ_И = φ_В + Е₂ ─ I₂∙ r₀₂ = 5,2 + 20 ─ 0,0608∙1 = 25,14 В,

φ_К = φ_И ─ I₂∙R₂ = 25,14 ─ 0,0608∙53 = 21,92 В,

φ_А = φ_К ─ Е₂ + I₁∙ r₀₁ = 21,92 ─ 40 + 0,3931∙1 = ─ 17,69 В,

φ_Б = φ_А + I₁∙R₁ = ─ 17,69 + 0,3931∙45 = 0 В – проверочная точка.

Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, по оси ординат – потенциалы точек с учетом их знака в соответствии с рисунком 7.

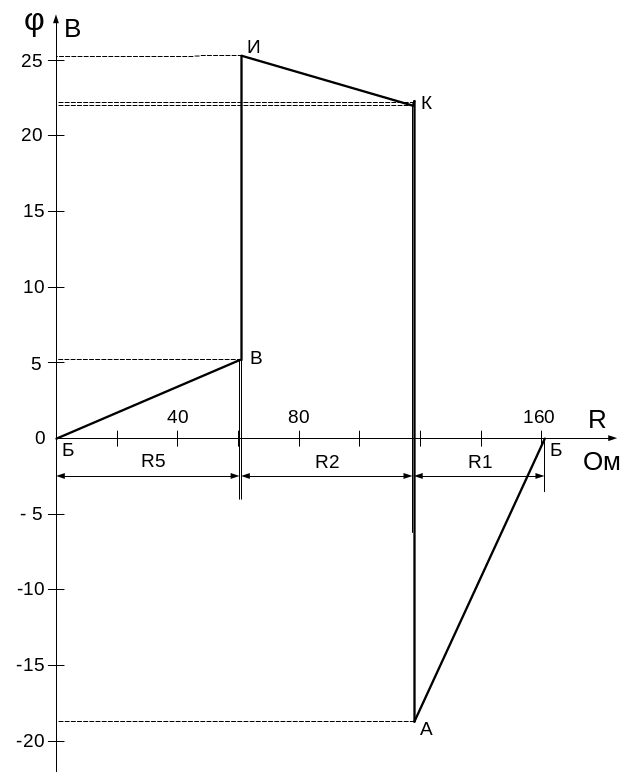
Рисунок 7 – Потенциальная диаграмма замкнутого контура