1.2 Расчет токов в ветвях схемы методом контурных токов

Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе до (n─1).

Для составления уравнений выделяем в схеме три независимых контура (I, II, III). Для каждого указанного контура произвольно зададимся расчетной величиной – контурным током Iк1, Iк2, Iк3 и его направлением в соответствии с рисунком 3. На этом же рисунке произвольно укажем направление тока в каждой ветви.

Рисунок 3 – Схема электрической цепи к расчету методом контурных

токов

При составлении уравнений по второму закону Кирхгофа, в левой части равенства будем записывать алгебраическую сумму ЭДС источников, входящих в выделенный контур, а в правой части равенства будем алгебраически суммировать напряжения на сопротивлениях, входящих в этот контур, а также учитывать падение напряжений на сопротивлениях смежной ветви, создаваемых контурным током соседнего контура.

С учетом выше изложенного, система уравнений будет иметь следующий вид

Е₁ = I_К1∙(R₁ + r_{0 1}+ R₃ + R₄) ─ I_К2∙(R₁ + r₀₁) ─ I_К3∙R₄

Е₂ ─Е₁ = ─ I_К1∙(R₁ + r₀₁) + I_К2∙(R₁ + r₀₁ + R₂ + r₀₂ + R₅) ─ I_К3∙R₅

0 = ─ I_К1∙R₄ ─ I_К2∙R₅ + I_К3∙(R₄ + R₅ + R₆)

Подставляем в полученные уравнения числовые значения ЭДС и сопротивлений. Полученную систему уравнений решим с помощью определителей.

40 = 102∙I_К1 ─ 46∙I_К2 ─ 24∙I_К3,

─20 = ─ 46∙I_К1 + 161∙I_К2 ─ 61∙I_К3,

0 = ─ 24∙I_К1 ─ 61∙I_К2 + 100∙I_К3

Сначала вычисляем главный определитель системы Δ, затем частные определители Δ1, Δ2, Δ3.

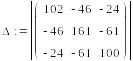_{= 823634,}

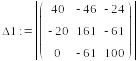
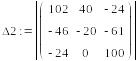_{= 373880,}

_{= 50080,}

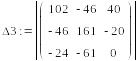_{= 120280}

Затем вычисляем контурные токи

Iк₁ = Δ₁ / Δ = 373880 / 823634 = 0,4539,

Iк₂ = Δ₂ / Δ = 50080 / 823634 = 0,0608,

Iк₃ = Δ₃ / Δ = 120280 / 823634 = 0,146

Далее определяем токи в ветвях I₁, I₂, I₃, I₄, I₅, I₆, используя полученные расчетные значения контурных токов Iк₁, Iк₂ и Iк₃. При этом если ветвь контура не входит в другие контуры, то действительный ток в ней равен расчетному контурному току. В ветвях, принадлежащих двум смежным контурам, действительный ток определяется как алгебраическая сумма контурных токов смежных контуров с учетом их направления.

I₁ = I_К1 - I_К2 = 0,4539 - 0,0608 = 0,3931,

I₂ = I_К2 = 0,0608,

I₃ = I_К1 = 0,4539,

I₄ = I_К3 - I_К1 = 0,146 - 0,4539 = - 0,3079,

I₅ = I_К3 - I_К2 = 0,146 - 0,0608 = 0,0852,

I₆ = I_К3 = 0,146

1.3 Расчет токов во всех ветвях схемы методом наложения

По методу наложения ток в любой ветви рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.

1.3.1 Определим частные токи во всех ветвях, приравняв нулю ЭДС Е₁ в соответствии с рисунком 4.

Рисунок 4 – Схема электрической цепи к расчету методом наложения при ЭДС Е₁ = 0

Тогда система уравнений, составленных на основании первого и второго законов Кирхгофа, будет иметь вид

0 = I₁ + I₂ ─ I₃,

0 = I₁ + I₄ ─ I₅,

0 = I₂ + I₅ ─ I₆,

Е₂ = ─ I₁∙(R₁ + r₀₁) + I₂∙(R₂ + r₀₂) ─ I₅∙R₅,

0 = I₁∙(R₁ + r₀₁) + I₃∙R₃ ─ I₄∙R₄,

0 = I₄∙R₄ + I₅∙R₅ + I₆∙R₆

Подставляем в полученные уравнения числовые значения ЭДС и сопротивлений.

0 = I₁ + I₂ ─ I₃,

0 = I₁ + I₄ ─ I₅,

0 = I₂ + I₅ ─ I₆,

20 = ─ I₁∙46 + I₂∙54 ─ I₅∙61,

0 = I₁∙46 + I₃∙32 ─ I₄∙24,

0 = I₄∙24 + I₅∙61 + I₆∙15

Полученную систему уравнений решаем с использованием определителей.

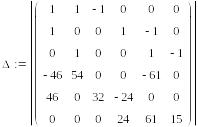= 823634,

= ─ 71200,

= 192480,

= 121280,

= 25240,

= ─ 45960,

= 146520

Затем вычисляем частные токи в ветвях

I'₁ = Δ1 / Δ = ─ 71200 / 823634 = ─ 0,0864,

I'₂ = Δ2 / Δ = 192480 / 823634 = 0,2337,

I'₃ = Δ3 / Δ = 121280 / 823634 = 0,1472,

I'₄ = Δ4 / Δ = 25240 / 823634 = 0,0306,

I'₅ = Δ5 / Δ = ─ 45960 / 823634 = ─ 0,0558,

I'₆ = Δ6 / Δ = 146520 / 823634 = 0,1779

1.3.2 Определим частные токи во всех ветвях, при ЭДС Е₂ = 0 в соответствии с рисунком 5).

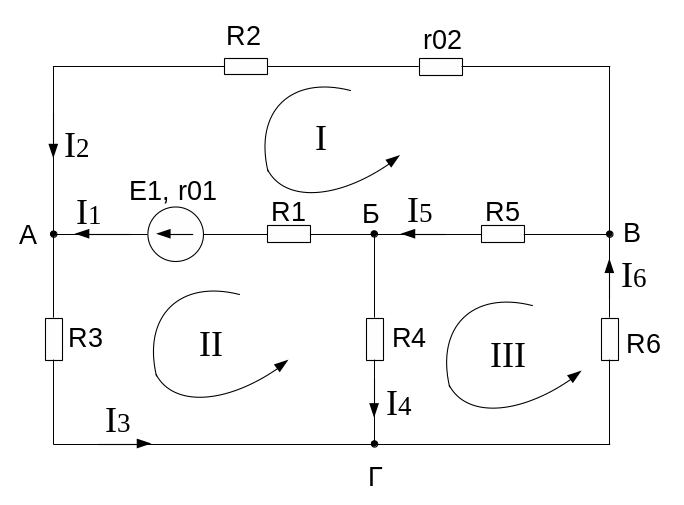
Рисунок 5 – Схема электрической цепи к расчету методом наложения при ЭДС Е₂ = 0

Тогда система уравнений, составленных на основании первого и второго законов Кирхгофа, будет иметь вид

0 = I₁ + I₂ ─ I₃,

0 = I₁ + I₄ ─ I₅,

0 = I₂ + I₅ ─ I₆;,

─Е1 = ─ I₁∙(R1+r01) + I₂∙(R2+r02) ─ I₅∙R5,

Е1 = I₁∙(R1+r01) + I₃∙R3 ─ I₄∙R4,

0 = I₄∙R4 + I₅∙R5 + I₆∙R6

Подставляем в полученные уравнения числовые значения ЭДС и сопротивлений.

0 = I₁ + I₂ ─ I₃,

0 = I₁ + I₄ ─ I₅,

0 = I₂ + I₅ ─ I₆,

─40 = ─ I₁∙46 + I₂∙54 ─ I₅∙61,

40 = I₁∙46 + I₃∙32 ─ I₄∙24,

0 = I₄∙24 + I₅∙61 + I₆∙15

Полученную систему уравнений решаем с использованием определителей .

= 823634,

= 391000,

= ─ 142400,

= 252600,

= ─ 278840,

= 116160,

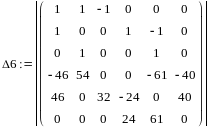= ─ 26240

Затем вычисляем частные токи в ветвях I", А

I"₁ = Δ1 / Δ = 395000 / 823634 = 0,4796,

I"₂ = Δ2 / Δ = ─ 142400 / 823634 = ─ 0,1729,

I"₃ = Δ3 / Δ = 252600 / 823634 = 0,3067,

I"₄ = Δ4 / Δ = ─ 278840 / 823634 = ─ 0,3385,

I"₅ = Δ5 / Δ = 116160 / 823634 = 0,141,

I"₆ = Δ6 / Δ = ─ 26240 / 823634 = ─ 0,0319

Определяем токи ветвей исходной цепи в соответствии с рисунком 2, выполняя алгебраическое сложение частных токов с учетом их знаков.

I₁ = I'₁ + I"₁ = ─ 0,0864 + 0,4796 = 0,3932,

I₂ = I'₂ + I"₂ = 0,2337 ─ 0,1729 = 0,0608,

I₃ = I'₃ + I"₃ = 0,1472 + 0,3067 = 0,4539,

I₄ = I'₄ + I"₄ = 0,0306 ─ 0,3385 = ─ 0,3079,

I₅ = I'₅ + I"₅ = ─ 0,0558 + 0,141 = 0,0852,

I₆ = I'₆ + I"₆ = 0,1779 ─ 0,0319 = 0,146