
- •Методические рекомендации
- •Содержание
- •1 Методики расчета линейных электрических цепей постоянно тока
- •1.1 Расчет токов в ветвях схемы методом узловых и контурных уравнений
- •1.2 Расчет токов в ветвях схемы методом контурных токов
- •1.3 Расчет токов во всех ветвях схемы методом наложения
- •1.4 Сравнительная оценка результатов расчетов токов в ветвях различными методами
- •1.5 Расчет баланса мощностей для заданной электрической цепи
- •1.6 Построение потенциальной диаграммы
- •2 Расчет однофазных линейных электрических цепей переменного тока
- •2.1 Расчет емкостей конденсаторов и индуктивностей катушек
- •2.2 Расчет сопротивлений
- •2.3 Расчет токов в ветвях цепи
- •2.4 Расчет напряжений на элементах заданной электрической цепи
- •2.5 Расчет показания вольтметра
- •2.6 Расчет полной мощности цепи
- •2.7 Расчет активной и реактивной мощностей приемников
- •2.8 Расчет коэффициента активной мощности цепи Cos φ
- •2.8 Уравнения мгновенных значений токов в узле а
- •2.9 Построение векторных диаграмм токов и напряжений
- •3 Расчет трехфазных линейных электрических цепей переменного тока
- •3.1 Схема соединения сопротивлений звездой
- •3.1.1 Расчет фазных сопротивлений
- •3.1.2 Расчет фазовых токов
- •3.1.3 Расчет мощностей
- •3.1.4 Расчет напряжений на элементах трехфазной цепи
- •3.1.5 Уравнения мгновенных значений фазовых токов
- •3.1.6 Построение векторных диаграмм для токов и напряжений
- •3.2 Схема соединения сопротивлений треугольником
- •3.2.1 Расчет фазных сопротивлений
- •3.2.2 Расчет фазовых и линейных токов
- •Приложение а
- •Приложение в
- •Приложение д
- •Приложение ж
- •Образец оформления титульного листа к курсовому проекту
1 Методики расчета линейных электрических цепей постоянно тока
Методики расчета линейных электрических цепей постоянно тока рассмотрим на примере расчета электрической цепи, в соответствии с рисунком 1.
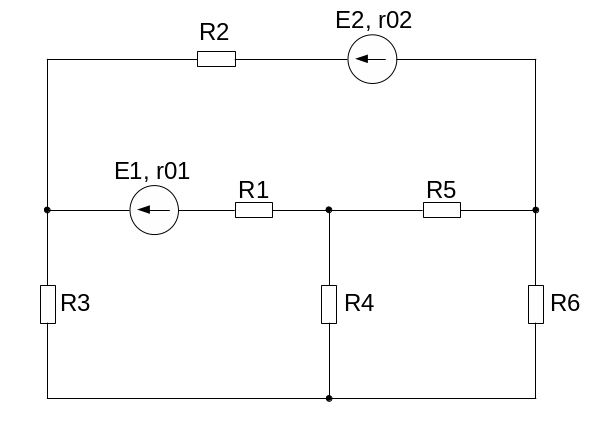
Рисунок 1 – Схема электрической цепи постоянно тока
Изображенная на рисунке 1 электрическая цепь имеет следующие параметры: Е1 = 40 В, Е2 = 20 В, R1 = 45 Ом, R2 = 53 Ом, R3 = 32 Ом, R4 = 24 Ом, R5 = 61 Ом, R6 = 15 Ом, r01 = 1 Ом, r02 = 1 Ом.
Требуется определить:
- токи во всех ветвях схемы на основании законов Кирхгофа;
- токи во всех ветвях схемы, используя метод контурных токов;
- токи во всех ветвях схемы, используя метод наложения;
- составить баланс мощностей для заданной схемы;
- построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
Исходные данные к задаче 1 приведены в приложении А, Б.
1.1 Расчет токов в ветвях схемы методом узловых и контурных уравнений
Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой электрической цепи.
При расчете данным методом произвольно задаем направление токов в ветвях: I1, I2, I3, I4, I5, I6 (в соответствии с рисунком 2).
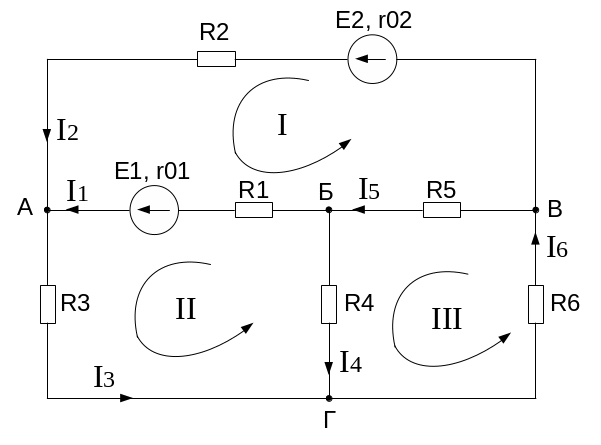
Рисунок 2 – Схема электрической цепи к расчету методом узловых и контурных уравнений
Далее составляем систему уравнений. В системе должно быть столько уравнений, сколько в рассчитываемой цепи ветвей (неизвестных токов).
В заданной цепи шесть ветвей. Значит, в системе должно быть шесть уравнений. Сначала составляем уравнения для трех узлов по первому закону Кирхгофа. Для цепи с n узлами можно составить (n ─ 1) независимых уравнений. В нашей цепи четыре узла (А, Б, В, Г), значит, число уравнений (n─1)=(4─1)=3. Составляем три уравнения для любых трех узлов, например, для узлов А, Б и В.
Для узла А: 0 = I1 + I2 ─ I3.
Для узла Б: 0 = I1 + I4 ─ I5.
Для узла В: 0 = I2 + I5 ─ I6.
Три недостающих уравнения составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие.
Задаемся обходом каждого контура против часовой стрелки и составляем уравнения по второму закону Кирхгофа.
Для контура I:
Е2 ─ Е1 = ─ I1∙(R1 + r01) + I2∙(R2 + r02) ─ I5∙R5.
Для контура II:
Е1 = I1∙(R1+r01) + I3∙R3 ─ I4∙R4.
Для контура III:
0 = I4∙R4 + I5∙R5 + I6∙R6.
ЭДС в контуре берется со знаком «+», если направление ЭДС совпадает с направлением обхода контура, если не совпадает, то ставится знак «─».
Падение напряжения на сопротивлении контура берется со знаком «+», если направление тока в нем совпадает с направлением обхода контура, если не совпадает, то ставится знак «─».
Мы получили систему уравнений из шести уравнений с шестью неизвестными токами I1, I2, I3, I4, I5, I6.
 0 = I1
+ I2
─ I3,
0 = I1
+ I2
─ I3,
0 = I1 + I4 ─ I5,
0 = I2 + I5 ─ I6,
Е2 ─Е1 = ─ I1∙(R1+r01) + I2∙(R2+r02) ─ I5∙R5,
Е1 = I1∙(R1+r01) + I3∙R3 ─ I4∙R4,
0 = I4∙R4 + I5∙R5 + I6∙R6
Подставляем в полученные уравнения числовые значения ЭДС и сопротивлений
0 = I1 + I2 ─ I3,
0 = I1 + I4 ─ I5,
0 = I2 + I5 ─ I6,
─20 = ─ I1∙46 + I2∙54 ─ I5∙61,
40 = I1∙46 + I3∙32 ─ I4∙24,
0 = I4∙24 + I5∙61 + I6∙15
Полученную систему уравнений решаем с использованием определителей Крамера.
Сначала вычисляем главный определитель системы Δ, затем частные определители Δ1, Δ2, Δ3, Δ4, Δ5, Δ6.
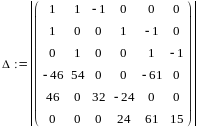 =
823634,
=
823634,
 =
323800,
=
323800,
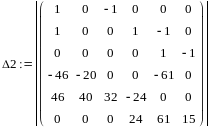 =
50080,
=
50080,
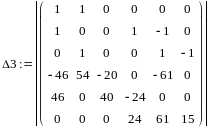 =
373880,
=
373880,
 = ─ 253600,
= ─ 253600,
 =
70200,
=
70200,
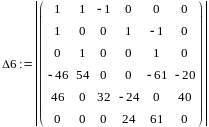 =
120280
=
120280
Затем вычисляем токи в ветвях
I1 = Δ1 / Δ = 323800 / 823634 = 0,3931 А,
I2 = Δ2 / Δ = 50080 / 823634 = 0,0608 А,
I3 = Δ3 / Δ = 373880 / 823634 = 0,4539 А,
I4 = Δ4 / Δ = ─ 253600 / 823634 = ─ 0,3079 А,
I5 = Δ5 / Δ = 70200 / 823634 = 0,0852 А,
I6 = Δ6 / Δ = 120280 / 823634 = 0,146 А
