Пассивные компоненты и их модели Резистор

Вольтамперная характеристика реального резистора на постоянном токе не отличается от идеальной. При создании высокочастотной модели необходимо учитывать особенности изготовления. За счет наличия индуктивности выводов и резистивного слоя сопротивление резисторов на высокой частоте становится комплексным, приобретает индуктивный характер:

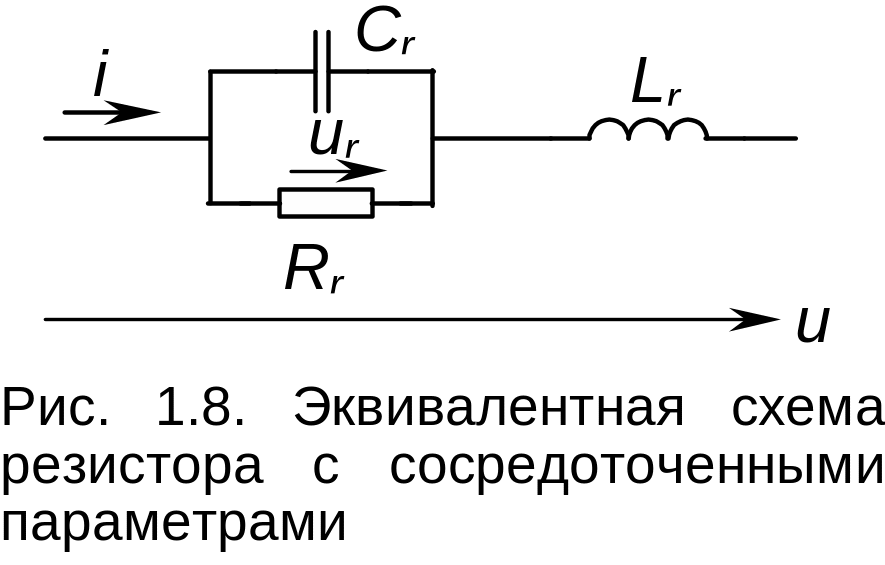
С повышением частоты проявляются также емкостные свойства резистора – в основном емкость между его выводами. Таким образом эквивалентная схема с сосредоточенными параметрами имеет вид (рис. 1.8):

В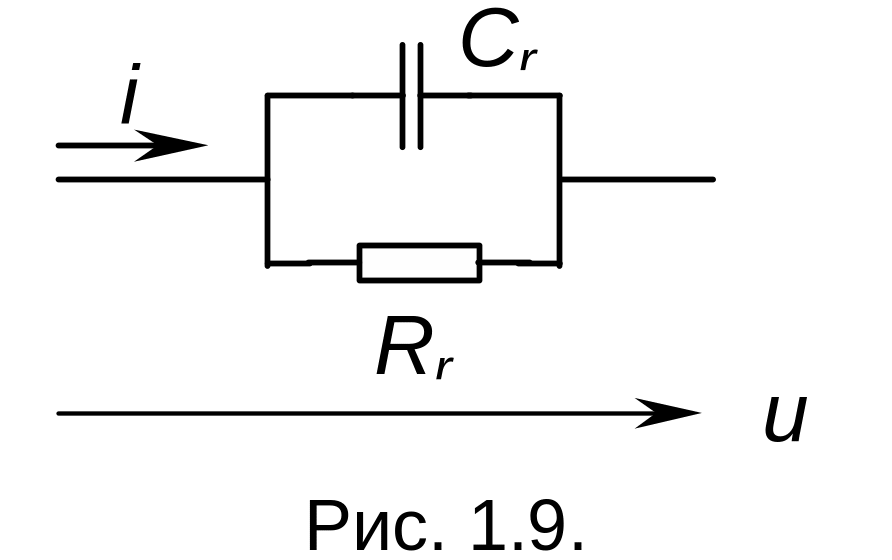 принципе, параметры резистора долины быть распределенными, однако их учет значительно усложняет анализ и применяется лишь при работе на СВЧ и при расчете элементов в гибридном исполнении. Приведенную эквивалентную схему можно описать системой 2-х дифференциальных уравнений:

Здесь С_r, L_r – величины паразитных параметров, u_r – напряжение на активной составляющей резистора. В зависимости от соотношения параметров эквивалентная схема резистора может быть упрощена. Для высокоомных резисторов, у которых , т.е. активное сопротивление значительно больше волнового, можно пренебречь его индуктивной составляющей. При этом модель принимает вид (рис. 1.9):

Полное сопротивление синусоидальному сигналу можно найти из расчета:

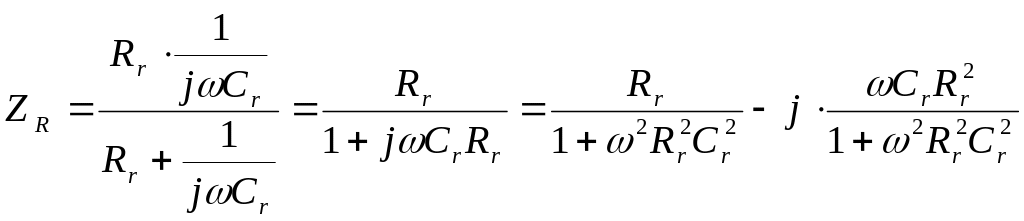
Здесь первое слагаемое — активная составляющая полного сопротивления, второе — реактивная составляющая. При 0, Z_rR_r, при  . Для низкоомных резисторов , можно пренебречь емкостной составляющей комплексного сопротивления. При этом схема имеет вид (рис. 1.10):

У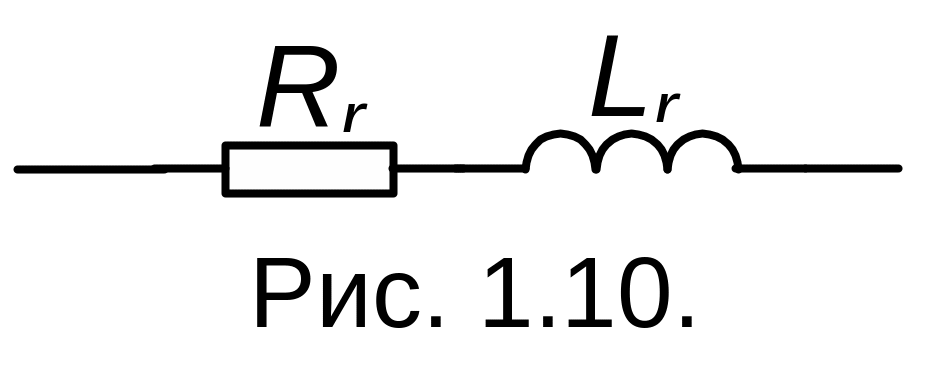 казанную особенность необходимо учитывать при проектировании схем, особенно СВЧ.

Электрические конденсаторы

В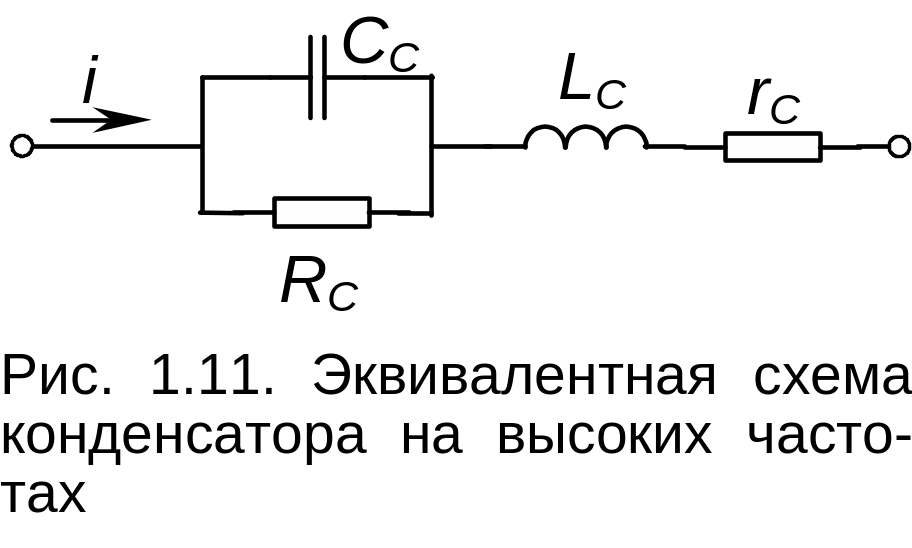 электронике конденсаторы выполняют в виде токопроводящих обкладок, разделенных диэлектриком. Величина емкости зависит от площади обкладок S и  диэлектрика. Различают конденсаторы с газообразным, жидким, твердым, окcидным диэлектриком. На высоких частотах необходимо учитывать потери в диэлектрике, токи утечки, индуктивное сопротивление обкладок и выводов. Эквивалентная схема конденсатора на высоких частотах имеет вид (рис. 1.11):

Полное сопротивление конденсатора зависит от частоты и определяется по формуле:

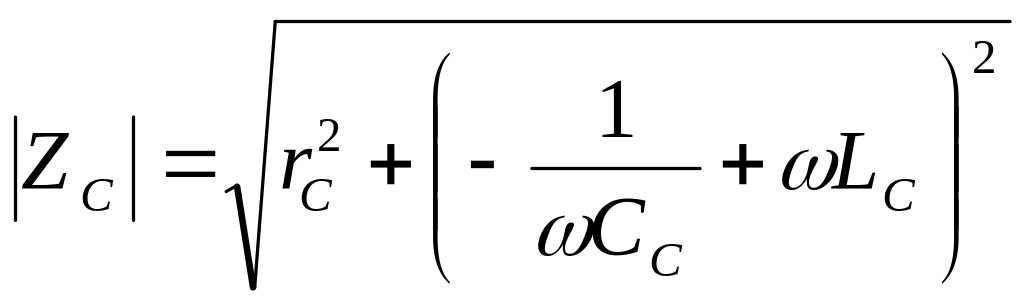
З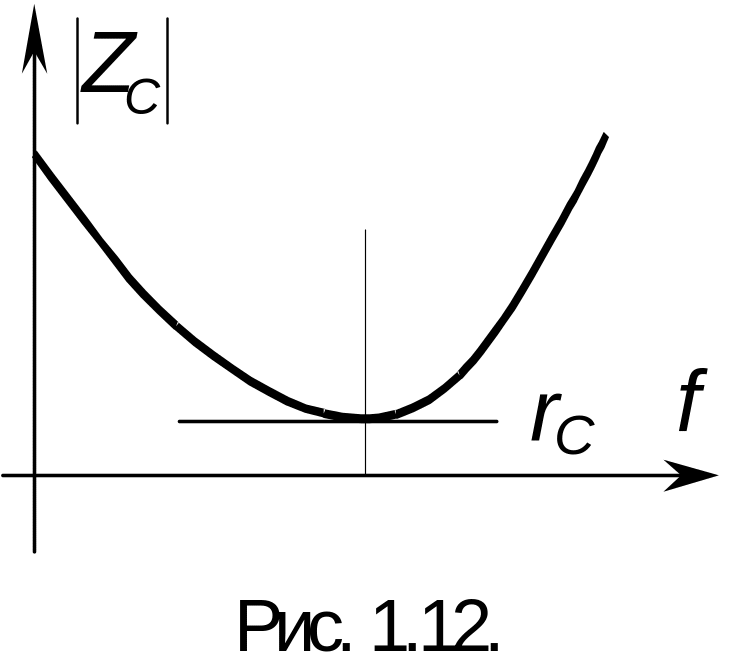 десь сделано допущение о том, что R_C>>r_C, что справедливо на высоких частотах практически всегда. Сопротивление утечки R_C учитывается, как правило, лишь в прецизионных схемах и при расчете медленных процессов. Зависимость Z_C(f) в соответствии с приведенным соотношением имеет вид (рис. 1.12):

Таким образом, после резонансной частоты сопротивление конденсатора приобретает индуктивный характер. Следует отметить, что для электролитических конденсаторов величина емкости непостоянна, а также зависит от частоты работы, что объясняется процессами поляризации диэлектрика. Можно предложить аппроксимацию зависимости С_С(f) в виде:

,

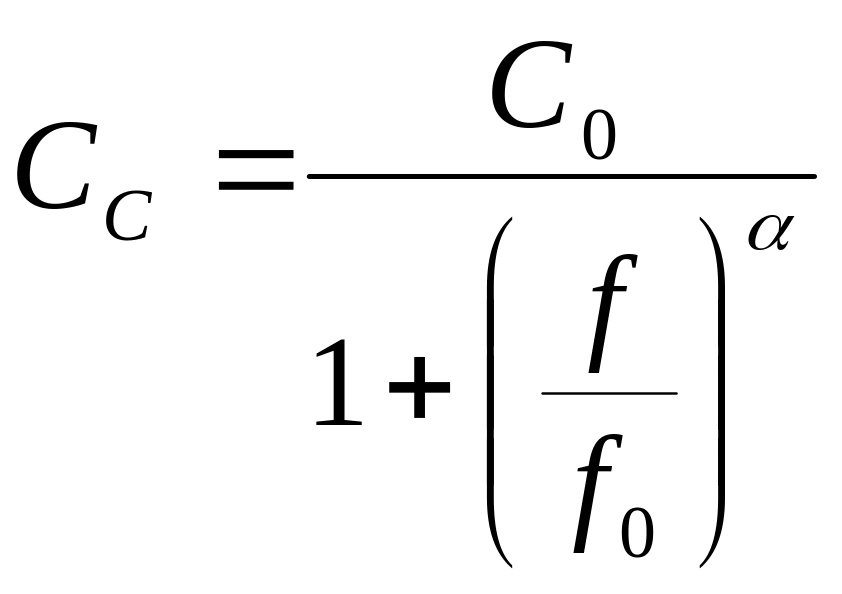где C₀ – номинальная емкость конденсатора, f₀ – частота, на которой емкость падает вдвое,  - некоторый коэффициент, учитывающий скорость спада емкости.