Интеграл Дюамеля

Импульсная функция и импульсная характеристика системы очень удобны для расчета реакции системы. Однако более наглядным является представление воздействия с помощью ступенчатой функции 1(t) (рис. 3.15).

И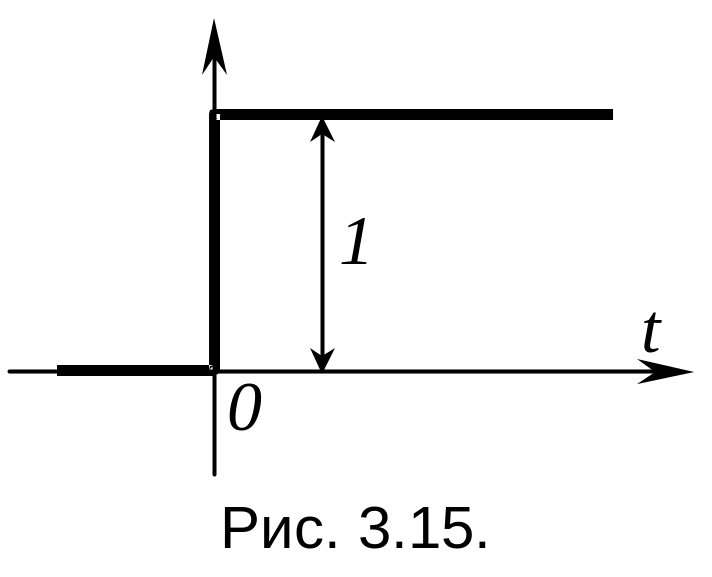 зображением 1(t) является, очевидно 1/p (можно найти из прямого преобразования Лапласа). Для нахождения реакции f₂(t) будем рассматривать в операторном виде выражение:

Что такое ? Что является ее оригиналом во временной области?

Если , то . Тогда . Таким образом реакция системы на единичный скачок (переходная характеристика) h(t) имеет изображение по Лапласу H(p)/p, т.е.:

Операции деления изображения на p соответствует интегрирование оригинала, а оригиналом H(p) является импульсная характеристика g(t). Таким образом получаем:

Как, зная переходную характеристику, рассчитать переходный процесс при произвольном входном воздействии? Очевидно, реакция f₂(t) будет соответствовать свертке оригиналов f₁(t) и h(t), продифференцированной по времени за счет умножения на p (по теореме о дифференцировании оригинала):

По правилу дифференцирования интеграла с переменным верхним пределом:

.

Т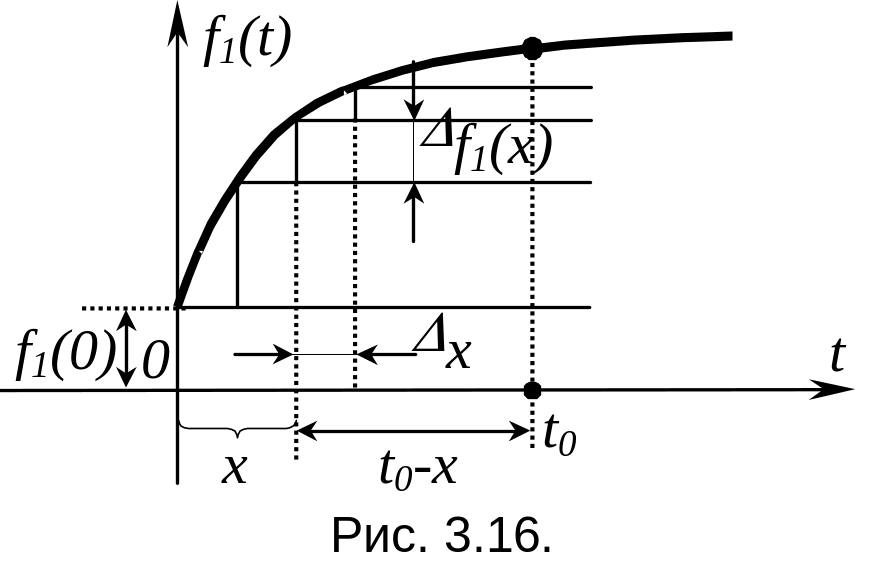 от же результат может быть получен несколько другим путем (из геометрического смысла интеграла Дюамеля). Сложное воздействие может быть представлено как некоторое ступенчатое воздействие, приложенное в нулевой момент времени, и ряд следующих друг за другом малых воздействий (см. рис. 3.16). Для линейных цепей справедлив принцип наложения. Если рассматривать реакцию схемы на воздействие в некоторый момент времени t₀, то эта реакция есть результат наложения реакции на первый импульс и суммы реакций на ряд бесконечно малых воздействий df₁(x)=f₁^'(x)dx. Тогда, интегрируя реакции за период времени от 0 до t₀, получим аналогичное выражение.

Т.к. момент времени, в который определяется реакция (t₀) не имеет существенного значения, то его заменяют на t.

Указанные соотношения называются интегралом Дюамеля.

Частотный метод анализа переходных процессов

Если f(t) — периодическая функция с периодом Т, удовлетворяющая условию Дирихле (т.е. может быть представлена в виде конечного числа интервалов, на которых функция монотонна и непрерывна, а между интервалами имеет разрывы 1-го рода), то она может быть представлена в виде суммы тригонометрического ряда (ряда Фурье):

, где ,

или

,

где ; ;

;

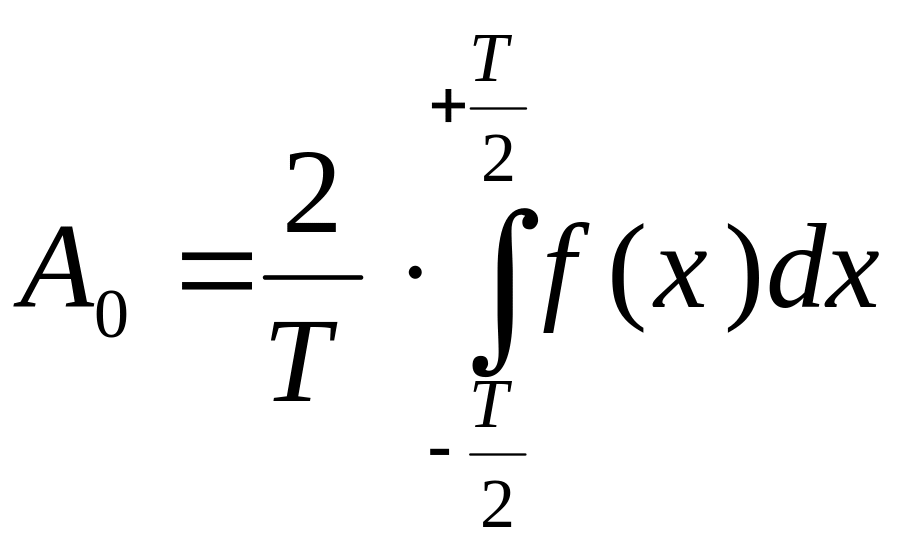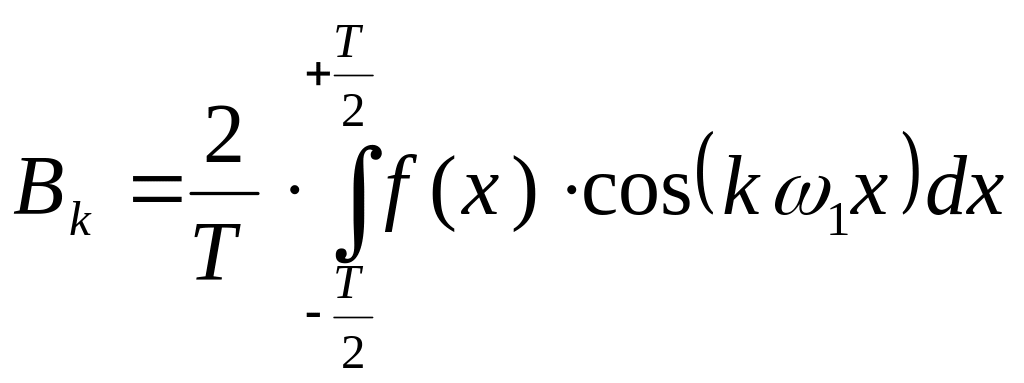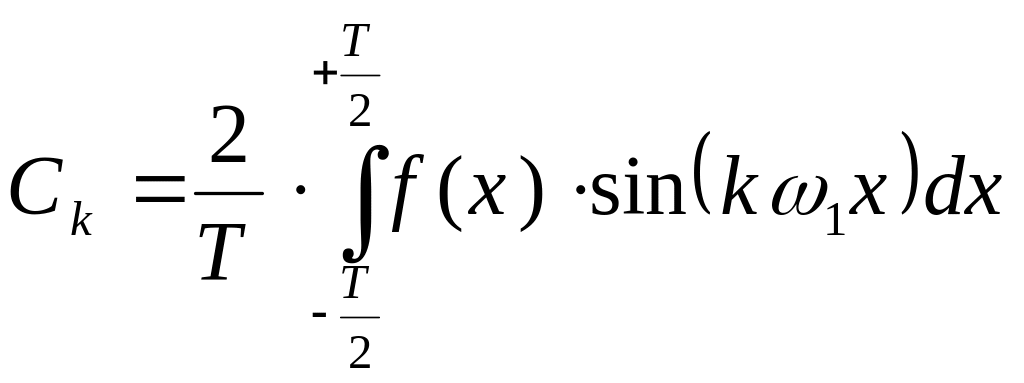
И спользуя известные равенства (формулы Эйлера) можно получить:

– ряд Фурье в комплексной форме,

где комплексные коэффициенты 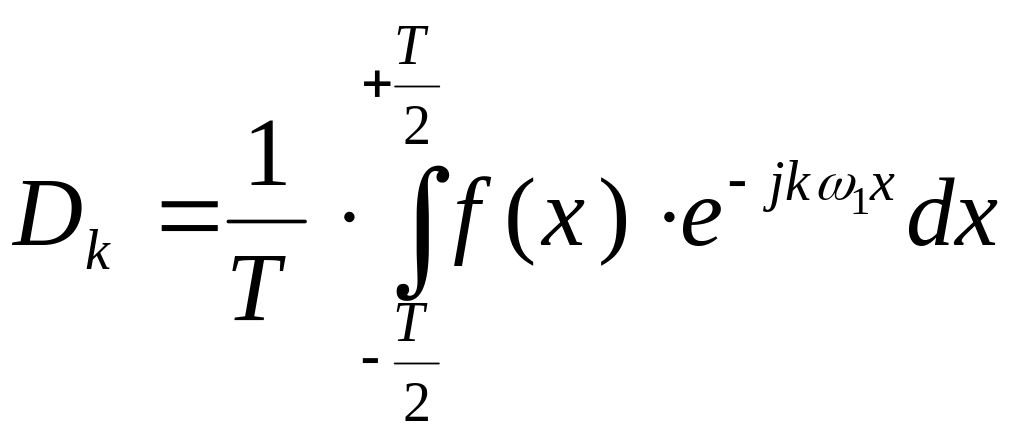, k=0, 1, 2, 3 ...

Р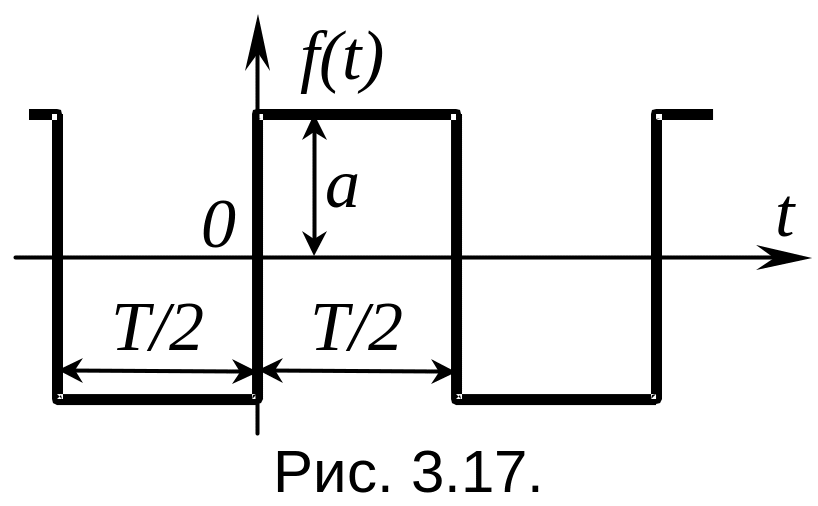 ассмотрим пример:

=

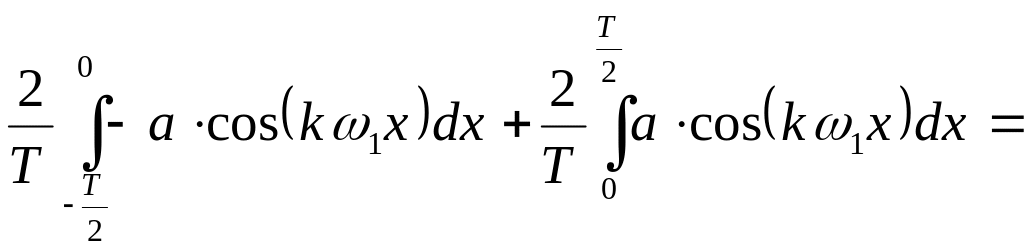
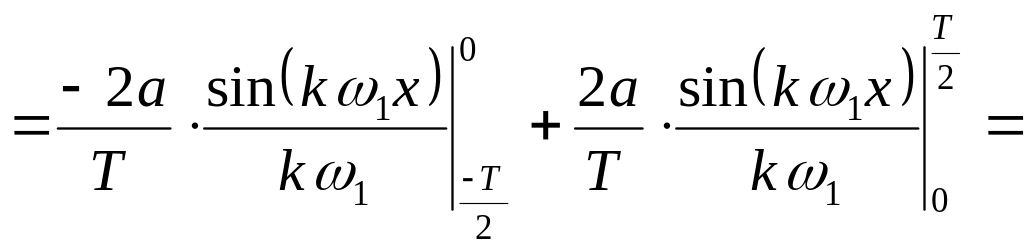
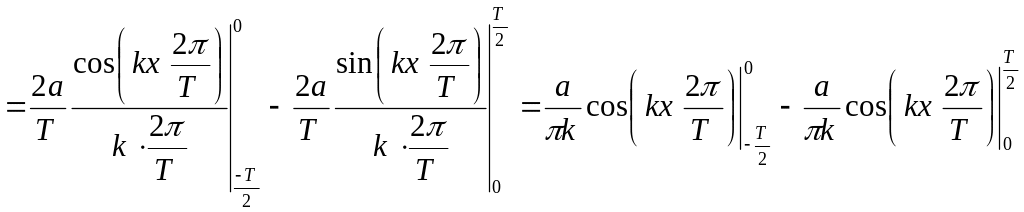
Пусть k - четное, т.е. k = 2m.

,

k – нечетное, т.е. k = 2m+1.

Таким образом,

, где k=1, 3, 5, …или

,

Итак, спектр амплитуд и фаз двуполярного меандра представлен на рис. 3.18.

Если f(x) — чётная, то разложение в ряд Фурье содержит только косинусные составляющие, если — нечетная, то синусные.

Пусть сигнал сдвинут во времени (запаздывает) на t₀.

Е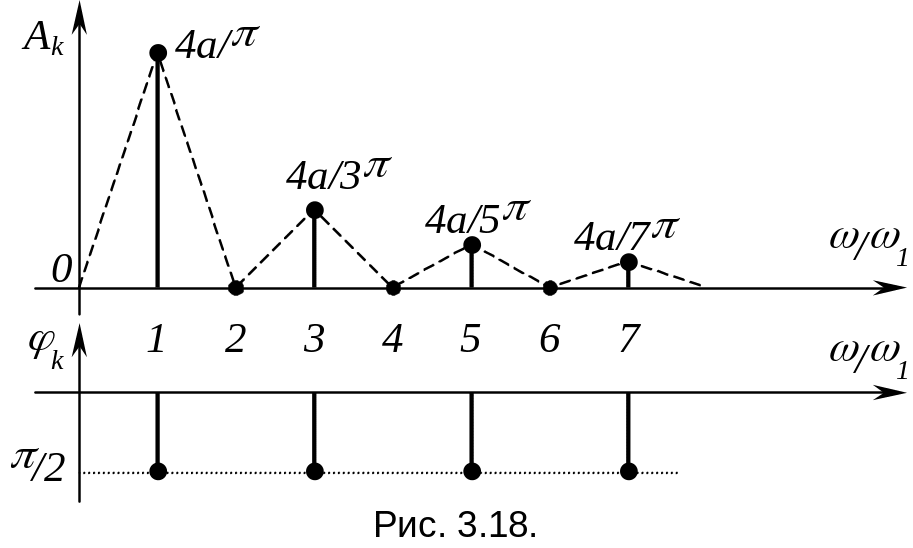 сли сигнал сдвинут, то необходимо лишь сдвинуть начальные фазы гармоник на угол k₁t_o.

Таким образом периодический сигнал можно описать амплитудами (А₀, A₁, A₂ ...) и фазами (₀, ₁, ₂ ...) гармоник, т.е. совокупностью частотных параметров. Закон распределения амплитуд и фаз называют спектром амплитуд и фаз.

Для периодической функции получаем дискретный (линейчатый) спектр амплитуд и фаз (см. рис. 3.18).

Ч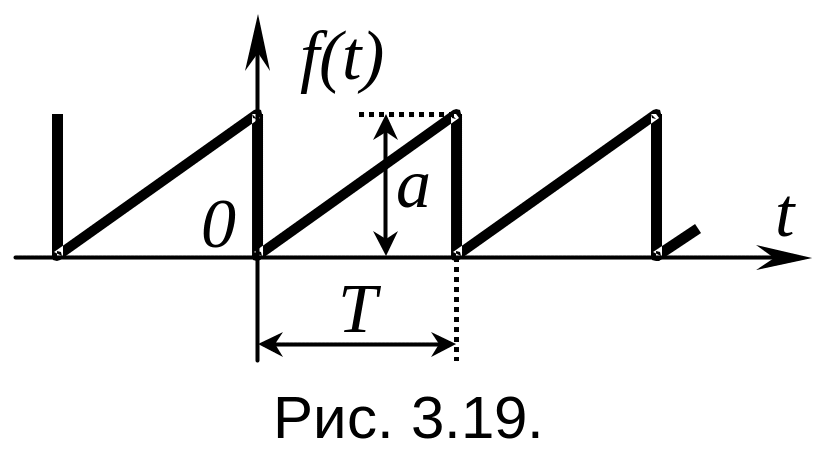 асто используемым в электронных устройствах сигналом является пилообразное напряжение (рис. 3.19). Его разложение в ряд Фурье:

Очень часто возникает вопрос об энергии, выделяемой негармоническим периодическим сигналом в активном сопротивлении. Предположим, что R=1, и к нему приложено напряжение u(t) = f(t). Мгновенная мощность:

Мощность средняя за период:

Т.к. интегрирование ведется в пределах периода и частоты всех гармоник кратны частоте сигнала (на периоде исходного сигнала укладывается целое число периодов гармоник), то несложно получить, что

Таким образом каждая гармоника выделяет в активном сопротивлении энергию, пропорциональную квадрату её амплитуды. Данное соотношение носит название равенства Парсеваля.

Так как энергия сигнала конечна, то несложно показать, что независимо от формы сигнала, если ряд Фурье существует, то амплитуда гармоники падает с ростом номера гармоники.