35.Опыт Эйнштейна и де Гааза. Спин. Полный момент импульса электрона.

Экспериментальное определение гиромагнитного отношения проведено в опытах Эйнштейна и де Гааза* (1915), которые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничении во внешнем магнитном поле (по обмотке соленоида пропускался переменный ток с частотой, равной частоте крутильных колебаний стержня). При исследовании вынужденных крутильных колебаний стержня определялось гиромагнитное отношение, которое ока­залось равным –(e/m). Таким образом, знак носителей, обусловливающих молекуляр­ные токи, совпадал со знаком заряда электрона, а гиромагнитное отношение оказалось в два раза большим, чем введенная ранее величина g (см. (131.4)). Для объяснения этого результата, имевшего большое значение для дальнейшего развития физики, было предположено, а впоследствии доказано, что кроме орбитальных моментов (см. (131.1) и (131.2)) электрон обладает собственным механическим моментом импульса L_es, называ­емым спином. Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. В настоящее время установлено, что спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона L_es, соответствует собственный (сотовый) магнитный момент р_ms, пропорци­ональный L_es и направленный в противоположную сторону:

(131.5)

*В. И. де Гааз (1878—1960) — нидерландский физик.

Величина g_s называется гиромагнитным отношением спиновых моментов.

Проекция собственного магнитного момента на направление вектора В может принимать только одно из следующих двух значений:

где ħ=h/(2) (h—постоянная Планка), _b—магнетон Бора, являющийся единицей магнитного момента электрона.

36. Сложение моментов. Результирующий момент многоэлектронной системы.

КВАНТОВОЕ СЛОЖЕНИЕ МОМЕНТОВ

- сложение моментов (орбитальных, спиновых, полных) независимых частиц (или систем - атомов, молекул и т. д.) по законам квантовой механики. Применяется также назв. векторное сложение моментов. В случае двух частиц задача состоит в определении спектра возможных собств. значений оператора квадрата суммарного момента   и его проекции   на фиксированную ось и соответствующих собств. ф-ций  - операторы моментов частиц 1,2). Спектр имеет вид  где квантовое число суммарного момента j может принимать значения j=j₁+j₂, j₁+j₂-1, ..., | j₁-j₂ |, а его проекции т=j, j -1, . . ., -j (j₁, m₁ и j₂, т₂ - квантовые числа моментов частиц 1 и 2 и их проекций). При этом каждое из возможных значений j встречается только один раз, что легко подтверждается подсчётом общего числа квантовых состояний (j, m): 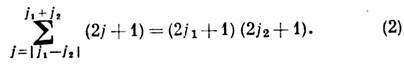На матeм. языке рассматриваемая задача соответствует разложению прямого (тензорного) произведения двух неприводимых представлений   группы вращений трёхмерного пространства SO(3) на неприводимые компоненты, что символически записывается в виде  (ряд Клебша - Гордана). Все значения j либо целые (когда j₁ и j₂ одновременно целые или полуцелые), либо полуцелые (когда один из складываемых моментов целый, а другой - полуцелый). В частности, для отд. электрона в атоме j всегда полуцелое: j=l+s, где квантовое число орбитального момента l=0, 1, 2, . . ., а спинового: s=1/2.Сложение произвольного числа N моментов

J=j₁+j₂+...+j_N(4)

может быть выполнено последоват. применением операции (1). В частности, наиб. значение J=j₁+j₂+...+j_N имеет кратность, равную единице (т. е. встречается в разложении прямого произведения   только один раз). В теории атомов применяются след. схемы сложения моментов: 1) связь Расселла - Саундерса (LS-связъ),в к-рой сначала складываются орбитальные и спиновые моменты отд. электронов: а затем L и S складываются в полный момент атома J; 2) jj -связь, в к-рой орбитальный и спиновый моменты i -го электрона складываются в полный момент электрона j_i=l_i+s_i, после чего полный момент атома J определяется по ф-ле (4). Условием применимости LS- связиявляется малость релятивистских взаимодействий по сравнению с эл.-статическим (кулоновским), поэтому она хорошо работает в лёгких атомах. По мере увеличения атомного номера Z роль релятивистских эффектов возрастает и происходит переход от LS -связи к jj- связи(однако в чистом виде последний тип связи фактически не встречается даже в самых тяжёлых атомах).Следует подчеркнуть, что только J и J_z -строго сохраняющиеся величины (соответствующие операторы коммутируют с гамильтонианом), в то время как l_i, L и S в схеме LS- связи, j_i в схеме jj -связи сохраняются лишь приближённо. <Для построения волновой ф-ции y_jm, отвечающей собств. значениям (1), из волновых ф-ций отд. частиц y_j1m1 и y_j2m2 используются Клебша - Гордана коэффициенты (или Вигнера 3j -символы). При сложении большего числа моментов применяются Вигнера6j-символы (или связанные с ними Рака коэффициенты )или 3nj -символы (при n/2).

Каждый электрон в атоме обладает орбитальным моментом импульса  и собственным моментом  Механические моменты связаны с соответствующими магнитными моментами, вследствие чего между всеми  имеется взаимодействие.

Моменты  складываются в результирующий момент атома  При этом возможны два случая.

1. Моменты  взаимодействуют между собой сильнее, чем с  которые в свою очередь сильнее связаны друг с другом, чем с  Вследствие этого все  складываются в результирующую  моменты  складываются в  а затем уже  дают суммарный момент атома  Такой вид связи встречается чаще всего и называется связью Рёссель — Саундерса или вязью.

2. Каждая пара  взаимодействует между собой сильнее, чем с другими  вследствие чего образуются результирующие для каждого электрона в отдельности, которые затем уже объединяются в  атома. Такой вид связи, называемый  вязью, наблюдается у тяжелых атомов.

Сложение моментов осуществляется по квантовым законам (см. § 24). Рассмотрим подробнее сложение моментов в случае связи Рёссель — Саундерса.

Орбитальные квантовые числа U всегда бывают целыми. Соответственно квантовое число L суммарного орбитального момента также бывает целым (либо нулем).

Квантовое число S результирующего спинового момента атома  может быть целым или полуцелым в зависимости от того, каким является число электронов в атоме — четным или нечетным. При четном числе электронов N квантовое число S принимает все целые значения от  «параллельны» друг другу) до нуля (все  попарно компенсируют друг друга). Так, например, при  может иметь значения 2, 1, 0. При нечетном N квантовое число S принимает все полуцелые значения от  «параллельны» друг другу) до  кроме одного, попарно компенсируют друг друга). Например, при  возможными значениями S будут: 

При данных  квантовое число J результирующего, момента  может иметь одно из следующих значений:

Следовательно,  будет целым, если S — целое (т. е. при четном числе электронов в атоме), и полуцелым, если S — полуцелое (т. е. при нечетном числе электронов).

Так, например,

1) в случае  возможные значения J равны 3, 2, 1;

2) в случае  возможные значения  равны 

Энергия атома зависит от взаимной ориентации моментов  (т. е. от квантового числа L), от взаимной ориентации моментов  (от квантового числа S) и от взаимной ориентации  квантового числа l). Условно терм атома записывается следующим образом:

где под L подразумевается одна из букв S, Р, D, F и т. д. в зависимости от значения числа L. Например, термы

относятся к состояниям с одинаковыми  одинаковыми  но различными J, равными 0, 1, 2.

Символ (32.1) содержит в себе сведения о значениях трех квантовых чисел L, S и . В случае, когда , стоящее слева вверху число  дает мультиплетность терма, т. е. количество подуровней, отличающихся значением числа J (см. (32.2)). В случае, когда  фактическая мультиплетность равна  Однако символ терма все равно пишут в виде (32.1), иначе он не содержал бы сведений о значении квантового числа 

Обозначениями типа (32.1) мы уже пользовались в § 29 применительно к атомам щелочных металлов. Однако для этих элементов характерно то, что S атома, совпадая с s валентного электрона, равно  Теперь же мы познакомились с символическими обозначениями термов для любых случаев.