40 Послідовність Фібоначчі

Послідо́вність Фібона́ччі, чи́сла Фібона́ччі — числова послідовність   задана рекурентним співвідношенням другого порядку

і т.д. Ця послідовність виникає у найрізноманітніших математичних ситуаціях - комбінаторних, числових, геометричних.

В природі числа Фібоначчі часто трапляються в різних спіральних формах. Так, черешки листя примикають до стебла по спіралі, що проходить між двома сусідніми листками: 1/3 повного оберту в ліщини, 2/5 - у дуба, 3/8 - у тополі і груші, 5/13 - у верби; лусочки на ялиновій шишці, насіння соняшника розташовані спіралями, причому кількості спіралей кожного напрямку також, як правило, числа Фібоначчі.

Числа Фібоначчі щільно пов'язані з золотим перетином 

Ідея полягає в наступному.

F_n = F_(n-1) + F_(n-2)

F_(n+1) = F_n + F_(n-1) = 2*F_(n-1) + F_(n-2)

Покладемо F₀ = 0, при цьому співвідношення при n = 2 залишиться істинним. Таким чином утворюється послідовність

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ..

41 За свідченням Месселя, античні зодчі в якості джерела гармонії архітектурних будівель незмінно використовували геометричні проекції п'яти так званих «Платонових тіл», що відображають відповідно до їхніх представлень загальну гармонію світу. Це вписані в сферу правильні багатогранники з числом граней 4, 6, 8, 12, 20.

Е. Мессель, зокрема, особливо виділяє пропорції, засновані на вписаному в коло правильному десятіугольніке. Ставлення радіусу кола до сторони багатокутника виражається ірраціональним числом (√ 5 +1) / 2 = 1,61 8 і дає пропорцію так званого «золотого перетину».

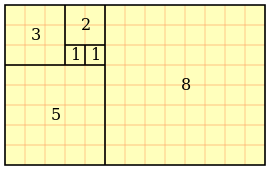
42 Динамічні прямокутники Хембіджа

Це послідовна система прямокутників, перший з яких є квадратом, а кожен наступний будується на стороні вихідного квадрата, рівною 7, і на діагоналі попереднього прямокутника. Виходить серія прямокутників, відношення сторін яких виражає ряд. У цій серії Хембідж розрізняє два види прямокутників-статичні і динамічні. У статичних прямокутників відносини сторін виражаються цілими числами, у динамічних - ірраціональними. Динамічні прямокутники, на думку Д. Хембіджа, виражають ідею зростання, руху і розвитку. З їх числа він насамперед виділяє три, у яких довгі сторони рівні Але особливе значення надає прямокутнику який безпосередньо пов'язаний з «золотим прямокутником» Хембідж проводить ретельне геометричне дослідження, виявляючи різноманітні прояви золотого перетину в системі прямокутника Досліджуючи геометрічекіе властивості цього прямокутника, він показує можливість його застосування для аналізу пропорцій об'єктів класичної архітектури і мистецтва

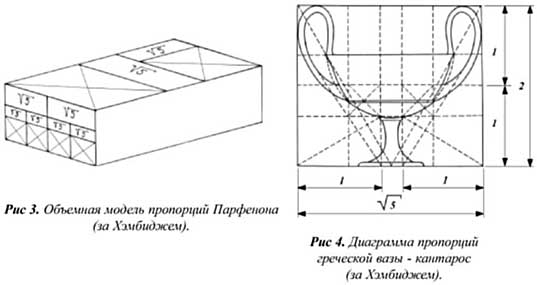
43.На основі подібності фігур за а.Тіршем.

 древних классических сооружениях и постройках средних веков пропорции, характерные для приведенных выше геометрических фигур, применялись как для назначения основных размеров сооружений в осях, главным образом в плане и иногда в разрезе (рис. 2), так и для назначения расстояний и просветов между элементами в основном на фасадах и в архитектурных деталях (рис. 1). В наше время построение пропорций в строительном проектировании основывается на работе А. Тирша «Справочник архитектора», где впервые приведены примеры практического применения теории пропорций, основанной на принципах подобия.