Теорія ймовірностей та математична статистика.

1. Емпіричні та теоретичні частоти.

2. Перевірка правдивості нульової гіпотези нормального закону розподілу.

3. Глибина моря вимірюється приладом, систематична помилка якого дорівнює нулю, а випадкові помилки розподілені нормально з середнім відхиленням 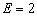м. Скільки потрібно зробити належних вимірювань, щоб визначити глибину з помилкою не більше 15 м при надійній ймовірності 90%.

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №26.

Теорія ймовірностей та математична статистика.

1. Критерій узгодженості Смирнова.

2. Модель експерименту. Однофакторний аналіз. Таблиця результатів спостереження.

3. Досвід показує, що опір на розрив дротів, вироблених деяким підприємством, можна розглядати як випадкову величину , нормально розподілену з середнім квадратичним відхиленням, яке дорівнює 15 кг/с. Вибірка об’єму 9 призводить до середнього опору 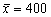кг/с. Нехай - середнє значення опору на розрив.

а) Перевірити при рівні значимості гіпотезу відповідно до альтернативної гіпотези .

б) Визначити об’єм вибірки так, щоб критерій мав потужність 0,99.

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №27.

Теорія ймовірностей та математична статистика.

1. Загальна дисперсія, міжгрупова та внутрішньо групова дисперсія. Незалежні оцінки дисперсії.

2. Загальний метод перевірки впливу фактора на ознаку способом порівняння дисперсій.

3. За даними 16 незалежних рівно точних вимірювань деякої фізичної величини знайдено середнє арифметичне результатів вимірювань 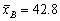і виправлене середнє квадратичне відхилення 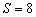. Знайти справжнє значення вимірюваної величини 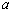з надійністю .

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №28.

Теорія ймовірностей та математична статистика.

1. Поняття про двофакторний дисперсійний аналіз.

2. Функціональна, статистична і кореляційна залежності. Рівняння парної регресії.

3. Досвід показує, що міцніть автопокришки можна вважати випадковою величиною (30000 км/800 км ). Вносяться зміни в технологічний процес. Вибірка з 100 покришок має 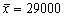км. На основі цієї вибірки при рівні значимості чи можна зробити висновок, що новий метод призводить до погіршення міцності покришок?

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №29.