Теорія ймовірностей та математична статистика.

1. Емпіричні початкові і центральні моменти, асиметрія й ексцес.

2. Точкові та інтервальні статистичні оцінки. Виправлена дисперсія.

3. Припустимо, що час роботи електрогенератора має щільність розподілу:

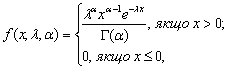
і термін роботи семи електрогенераторів дорівнює 100; 110; 175; 150; 185; 150; 185; 200; 220 г. Користуючись методом найбільшої правдоподібності, оцінити параметри і .

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №22.

Теорія ймовірностей та математична статистика.

1. Точність і надійність оцінки, визначення довірчого інтервалу.

2. Побудова довірчих інтервалів для 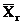за відомого σ_г і за невідомого.

3. Протягом 502 днів фіксувалась кількість автоматичних відхилень електродвигунів внаслідок перевантаження.

	0	1	2	3	4	5	6
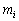
	120	148	133	66	28	4	1

У таблиці подано кількість днів, протягом яких спостерігалось відхилень. Перевірити, користуючись критерієм (Пірсона), гіпотезу про згоду даних спостережень з законом розподілу Пуассона, прийнявши рівень значимості .

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №23.

Теорія ймовірностей та математична статистика.

1. Побудова інтервалів для D_г . σ_г.

2. Визначення статистичної гіпотези. Нульова й альтернативна, проста й складна. Помилки першого і другого роду. Статистичний критерій, спостережене значення критерію.

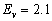3. Визначення швидкості снаряду було проведено на 5 випробуваннях, у результаті яких обчислено оцінку: м/с. Знайти 95%-й надійний інтервал, якщо відомо, що розсіювання швидкості підпорядковано нормальному закону з середнім відхиленням м/с.

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №24.

Теорія ймовірностей та математична статистика.

1. Критична область, область прийняття нульової гіпотези, критична точка. Загальна методика побудови правобічної, лівобічної та двобічної критичних областей.

2. Перевірка правдивості статистичних гіпотез: про рівність двох генеральних середніх, двох дисперсій, ознаки яких мають нормальні закони розподілу, про значення вибіркового коефіцієнта кореляції.

3. Термін служби деякого типу електроламп потужністю 100Вт можна розглядати як випадкову величину 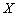з нормальним розподілом 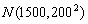. Вибірка з 25 таких ламп забезпечує середню тривалість горіння 1380 г.

а) При рівні значимості перевірити гіпотезу відповідно до альтернативної гіпотези .

б) Яка потужність критерію для .

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №25.