Теорія ймовірностей та математична статистика.

1. Експоненціальний закон та його використання у теорії надійності, теорії черг.

2. Рівномірний закон. Розподіл Х² , Х.

3. Партія виробів приймається, якщо ймовірність того, виріб виявиться бракованим, не перевищує 0,03. Серед випадково відібраних 400 виробів виявилось 18 бракованих. Чи можна партію прийняти?

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №17.

Теорія ймовірностей та математична статистика.

1. Розподіл Стьюдента, Фішера.

2. Нерівність Чебишева та її значення.

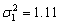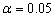3. Задача. Для порівняння точності двох приладів було виміряно деяку величину. За вимірюванням для першого приладу знайдено виправлену вибіркову дисперсію , за вимірюванням для другого приладу - . При рівні значимості перевірити, чи можна вважати точність приладів однаковою, чи другий прилад забезпечує більшу точність вимірювання.

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №18.

Теорія ймовірностей та математична статистика.

1. Теорема Чебишева, Бернуллі.

2. Центральна гранична теорема теорії ймовірностей (теорема Ляпунова).

3. Нехай - вибірка з генеральної сукупності, в якій ознака, що досліджується, є випадковою величиною з щільністю розподілу:

Користуючись методом найбільшої правдоподібності, оцінити параметри і .

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №19.

Теорія ймовірностей та математична статистика.

1. Визначення випадкового процесу та класифікація випадкових процесів. Закон розподілу й основні характеристики.

2. Пуассонівський потік та його властивості.

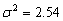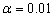3. Для певного класу приладів допустиме розсіяння показів . Для перевірки точності одного приладу виконано вимірювань деякої величини і отримано виправлену вибіркову дисперсію . При рівні значимості перевірити, чи можна вважати, що цей прилад відповідає вимогам стандарту?

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №20.

Теорія ймовірностей та математична статистика.

1. Генеральна та вибіркова сукупності. Статистичні розподіли вибірок. Полігон та гістограма.

2. Числові характеристики: вибіркова середня, дисперсія вибірки, середньоквадратичне відхилення, мода й медіана.

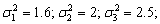
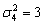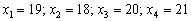3. Визначення діаметра втулки виконано чотирма способами, точність яких характеризується дисперсіями мм . Результати вимірювань: мм. Визначити наближене значення діаметра втулки і оцінити його точність.

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №21.