Теорія ймовірностей та математична статистика.

1. Умовні закони розподілу та їх числові характеристики. Визначення кореляційної залежності.

2. Система n випадкових величин, числові характеристики системи.

3. Задача. Ймовірність настання деякої події в кожному з незалежних випробувань рівна . Знайти ймовірність того, що кількість настання події задовольняє нерівність.

Варіанти 1–11: .

Варіанти 12–21: .

Варіанти 22–30: .

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №12.

Теорія ймовірностей та математична статистика.

1. Визначення функції випадкових величин. Функція дискретного випадкового аргументу та її числові характеристики.

2. Функції неперервного випадкового аргументу та її числові характеристики.

3. Задача. У першій урні білих і чорних кульок, в другій білих та чорних. З першої в другу переклали куль, потім з другої вийняли одну кулю. Знайти ймовірність того, що вийнята з другої урни куля – біла.

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №13.

Теорія ймовірностей та математична статистика.

1. Визначення функції розподілу ймовірностей та її густини для функцій двох випадкових елементів.

2. Визначення цілочислової випадкової величини. Ймовірна твірна функція та її властивості.

3. За допомогою радіодалекоміра проведено 9 незалежних вимірювань до цілі. Оцінити точність визначення відстані до цілі з надійністю , якщо точність вимірювання характеризується серединною помилкою 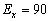м.

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №14.

Теорія ймовірностей та математична статистика.

1. Біноміальний, пуассонівський, геометричний та рівномірний закон розподілу.

2. Гіпергеометричний закон.

3. Цифри 0, 1, 2,..., 9 серед 800 перших десяткових знаків числа 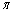з’явились відповідно 74, 92, 83, 79, 80, 73, 77, 75, 76, 91 раз. Перевірити за допомогою критерію гіпотезу про згоду цих даних з законом рівномірного розподілу при рівні значимості .

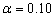Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №15.

Теорія ймовірностей та математична статистика.

1. Нормальний закон розподілу та його значення в теорії ймовірностей.

2. Логарифмічний нормальний закон. Гамма-розподіл.

3. За результатами 20 вимірювань визначено 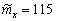м і м. Оцінити точність визначення дисперсії з надійністю 0,96.

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №16.