Теорія ймовірностей та математична статистика.

Події та їх класифікація. Операції над подіями. Поняття елементарної та складної випадкової події. Простір випадкових подій.
Класичне та статистичне визначення ймовірності, їх властивості.
Задача: кидають два гральні кубики. Знайти ймовірність того, що: а) сума очок не перевищує ; б) добуток очок не перевищує ; в) добуток очок ділиться на .

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №2.

Геометрична ймовірність.
Поняття залежності й незалежності випадкових подій. Умовна ймовірність та її властивості. Теорема про множення ймовірностей.
Задача. Є вироби чотирьох сортів, при цьому кількість виробів 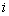-го сорту дорівнює 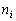, . Для контролю навмання беруть 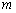виробів. Знайти ймовірність того, що серед них 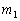першого сорту, і 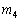другого, третього і четвертого відповідно .

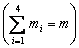Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №3.

Сумісні та несумісні події. Теорема додавання ймовірностей.
Повна група подій. Формула повної ймовірності.
Задача. Серед лотерейних білетів виграшних. Навмання взяли білетів. Знайти ймовірність того, що серед них 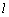виграшних.

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №4.

Формула Байєса.
Визначення повторних незалежних спроб. Формула Бернуллі.
Задача. У двох партіях 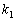і доброякісних виробів відповідно. Навмання вибирають по одному виробу з кожної партії. Яка ймовірність виявити серед них: а) хоча б один бракований; б) два браковані; в) один бракований і один якісний виріб?

Викладач к. психол.н. Жогно Ю.П.

Зав. каф. СДЗ та МП д.м.н. Аймедов К.В.

Білет №5.

Формула Байєса.
Визначення повторних незалежних спроб. Формула Бернуллі.
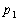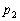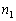Задача. Ймовірність того, що ціль вражена при одному пострілі першим стрільцем , другим – . Перший зробив , другий – 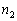пострілів. Знайти ймовірність, що ціль не вражена.