4.2 Логические функции

Английский математик Джордж Буль в середине 19-го столетия создал раздел алгебры, касающийся символической обработки логических отношений. Этот раздел алгебры, называе­мый Булевой алгеброй, оперирует величинами, которые могут иметь только два со­стояния: истина или ложь.

4.2.1 Инверсия или операция NOT (НЕ).

Инверсия обозначается символом надчеркивания. Таким образом, выражение означает, что переменная f является обратной величиной переменной А. То есть, если А = 0, то f = 1, и наоборот, если А = 1, то f = 0. На рисунке 4.2а эта зависимость представлена в виде таблицы истинности (truth table).

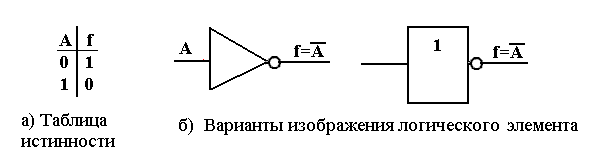
Рисунок 4.2 – Операция NOT

Общепринятое изоб­ражение элемента НЕ приведено на рисунке 4.2б. Кружок на изображении логи­ческих схем всегда означает инверсию и очень часто используется в сочетании с другими логическими элементами (см. например, рисунок 4.3в).

4.2.2 Операция AND.

Операция AND (И) реализует функцию «все или ничего». Результат операции будет истинным только в том случае, если оба входа истинны. На рисунке 4.3 име­ются две входные переменные. Опера­цию AND иногда называют операцией логического умножения, поскольку (по аналогии с обычным умножением) результат этой операции между любым битом и 0 всегда будет равен 0.

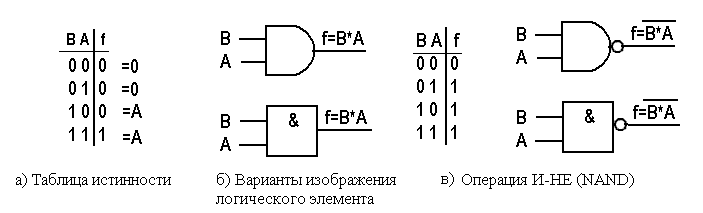
Рисунок 4.3 - Операция AND

4.2.3 Операция OR

Операция OR (ИЛИ) может использоваться, в тех случаях, когда нужно обнаружить ситуацию, что на всех входах нули, см. рисунок 4.4.

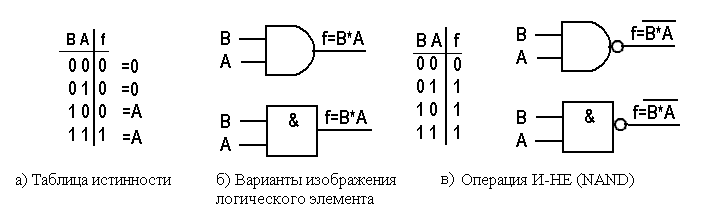
Рисунок 4.4 - Операция OR

Если предположить, что вход В является управляющим входом, а вход А — входом данных, то из рисунка 4.4а видно, что данные проходят через вентиль при В = 0 и задерживаются (на выходе постоянно 1) при В = 1.

4.2.4 Операция Exclusive OR – XOR ( Исключительно ИЛИ).

Функция XOR (Исключающее ИЛИ) истинна, ес­ли истинен только один из входов. Поэтому на символе изображено «=1», см. рисунок 4.5б. В отличие от обычной операции ИЛИ, при 1 на обоих входах на выходе будет 0.

Аналогично, из таблицы истинности операции Исключающее ИЛИ-НЕ (XNOR), показанной на рисунке 4.5в, видно, что выход такого элемента истинен при одинаковых сигналах на обоих входах. Таким образом, вентиль Исключающее ИЛИ-НЕ можно рассматривать в качестве однобитного компаратора.

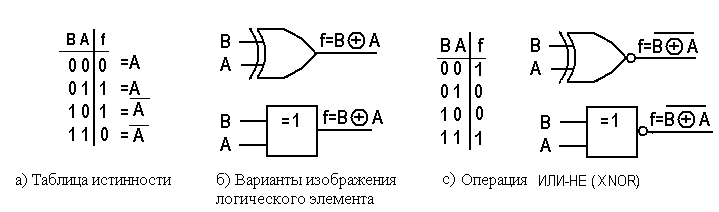
Рисунок 4.5 - Операция XOR

Исключающее ИЛИ и Исключающее ИЛИ-НЕ часто применяются для определения переполнения в знако­вом бите. Эта ситуация возникает, если знаковые биты (sign) обоих операндов одинаковы (S_B =S_A), а знаковый бит S_C результата отличается от них. Схема такого детектора, см. рисунок 4.6, описывается логи­ческой функцией:V=(S_BS_A)( S_BS_C).

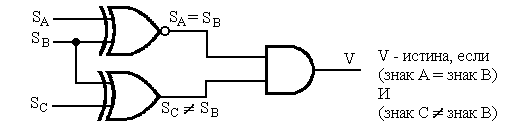
Рисунок 4.6 – Обнаружение переполнения в знаковом бите

5 Маскирование. Стек

Цель лекции: изучение маскирования, стека и его назначение.

Краткое содержание лекции. Использование логических функций для контроля и изменения значений регистров (маскирование). Счетчик команд и стек. Их работа при вызове подпрограмм.

5.1 Маскирование

При маскировании выполняется побитные логические операции разрядов исходного числа или проверки равенства чисел:

• логическая операция AND исходного числа и числа-маски очищает разряд числа в исходном числе, если в соответствующем разряде числа-маски записан 0, и не изменяет его, если в разряде маски записана единица;

• логическая операция OR исходного числа и числа-маски устанавливает в разряд исходного числа 1, если в таком же разряде маски будет записана 1, и не изменяет его, если в этом разряде маски записан 0;

• логическая операция XOR («исключающее ИЛИ») исходного числа и числа-маски инвертирует содержимое бита исходного числа, если в соответствующем разряде числа маски записана 1. И не изменяет его, если в этом разряде маски записан 0. Часто применяется для определения равенства регистра какому-либо числу, записанному в маске.

Примеры результатов маскирования приведены в таблице 5.1.

Т а б л и ц а 5.1 – Результаты маскирования

Объекты	Операция
	OR (установка с 4 по 7 бит)	AND (очистка с 0 по 3 бит)	XOR (биты с 0 по 3 не изменяем, инверсия с 4 по 7 бит)	XOR (проверка на равенство)
Число	10101010	10101010	10101010	11011101
Маска	11110000	11110000	11110000	11011101
Результат	11111010	10100000	01011010	00000000

Применяя маскирование, напишем программу регулирования расхода газа в установку для её нагрева без применения обратной связи.

Пусть определен требуемый расход газа (Treb_Raskhod), подаваемый в горелку установки при котором идет нормальный технологический процесс. Давление в трубе меняется, поэтому фактический расход (Fakt_Raskhod) не совпадает с требуемым расходом.

Вращая шток заслонки на трубе с помощью МЭО в сторону Bolshe, мы можем увеличить расход газа, вращая шток в сторону Menshe, мы можем уменьшить расход газа.

Сравнивая значения Treb_Raskhod и Fakt_Raskhod, будем определять направление вращения МЭО. Если Treb_Raskhod < Fakt_Raskhod заслонку надо прикрыть, если Treb_Raskhod > Fakt_Raskhod приоткрыть.

Подпрограмма определения направления "B" или "M" вращения МЭО.

В программе используется особенность кодировки латинских букв “М” и “В” в нулевом и первом разрядах.

MEO MOVF TREB_RASKHOD, W; требуемый расход --> W.

SUBWF FAKT_RASKHOD, W; W= Fakt_Raskhod - Treb_Raskhod.

MOVLW b'01001101'; записываем код буквы М, направление Menshe.

BTFSS STATUS, C; проверяем C = 1?

MOVLW b'01000010'; при C=0, записываем код буквы "В" (Bolshe).

MOVWF NAPRAV_MEO; запоминаем код символа направления.

ANDLW b'00000011'; маской оставляем только 0 и 1 разряды для МЭО.

MOVWF PORTC; пересылаем импульс управления на МЭО.

RETURN

С помощью применения операций AND и XOR можно определить, равны ли определенные биты входного числа заданному значению.

Пусть входное число в регистре PORTB равно 10101110. Три младших разряда контролируют состояние наличия в баке жидкости, заданной температуры и наличие нормального напряжения. Если эти три бита, равны 111, то открывается задвижка слива содержимого бака (это жидкий рубильник на 1000А с расплавом натрия).

MOVLW b’00000111’; заданное число-маска.

ANDWF PORTB, W; считываем из PORTB нужные биты в W.

XORLW b’00000111’; проверяем равенство их заданному числу.

BTFSC STATUS, Z; если Z = 0, пропускается следующая команда.

CALL SLIV; если Z = 1, вызываем подпрограмму SLIV.

MOVLW b’01100111’; дальнейшее продолжение программы.

В рассматриваемом случае подпрограмма SLIV не будет вызвана.