
- •1 Предмет мча.Особенности и задачи
- •Задачи Численного анализа
- •3. Решение нелинейных уравнений. Постановка задачи
- •4 Решение нелинейных уравнений. Отделение корней.
- •5. Решение нелинейных уравнений методом деления отрезка пополам.
- •6. Решение нелинейных уравнений методом простой итерации.
- •7. Условие сходимости мпи для нелинейных ур-ий.
- •8 Метод Ньютона.
- •9.Условие сходимости метода Ньютона
- •10. Модификация метода Ньютона для решения нелинейных ур-ний.
- •11. Решение нелинейных уравнений. Метод секущих
- •12. Решение нелинейных уравнений. Метод хорд.
- •13. Метод парабол.
- •14. Решение систем нелин.Ур-ий. Постановка задачи.
- •15. Решение систем нелин.Ур-ий. Отделение корней
- •16. Решение систем нелин.Ур-ий. Метод простой итерации
- •17. Решение систем нелин. Ур-ий. Метод релаксации.
- •18. Решение систем нелин.Ур-ий .Метод Ньютона
- •19. Решение си-м ура-нии методом Ньютона для 2х ур-нии.
- •20. Сходимость итерационного процесса
- •Когда матрица b и параметр не зависят от номера итерации то (3)
- •22. Постановка задачи интерполирования. Экстраполяция
- •23. Интерполирование алгебраическими многочленами
- •24. Интерполяционный полином Лагранжа. Методы записи.
- •25. Оценка погрешн. Интерп. Пол. Лагранжа. Примен. Пол. Лагранжа
- •26. Интерполяционная схема Эйткена
- •27. Конечные разности и разностные отношения
- •28. Интерполяционный многочлен Ньютона для неравномерной сетки
- •29. Интерполяционные формулы Ньютона для равномерной сетки
- •30. Сходимость интерполяционного процесса
- •31. Интерполирование сплайнами. Пострение кубического сплайна
- •32. Определение коэффициентов в кубическом сплайне.
- •33. Различные постановки задачи интерполирования
- •34. Многомерная интерполяция
- •35. Задача интерполяции в общей постановке
- •36. Наилучшее приближение функции, заданной таблично
- •37. Метод наименьших квадратов. Постановка задачи
- •38 Числ. Диференц. Конечными разност. Оценка погрешн. Источн. Погр.
- •39 Использ. Интерпо. Фо-мул для решен задачи числ. Дифференц
- •40 Улучшение аппроксим. Произв.(фо-лы Рунге-Ромберга)
- •41 Постановка задачи вычисл. Итегралов в квадратурах
- •42 Простейшие Квадратурные фо-лы. Оценка погрешности.
- •43 Числен. Интегр. С заран. Задан. Точн. Априорное нах. Шага интегрир.
- •44 Оценка точн. Квадр. Фо-лы по пр. Рунге Автом выбор шага интегрир.
- •45 Процесс Эйткина уточнения квадратурных формул
- •46 Квадрат. Фо-лы интерпол. Типа. Фо-лы ньютона-котеса
- •47 Квадр. Фо-л наивысш. Алгебр степени точн. Кв. Форм типа Гаусса
- •48 Приближенное выч-е интегралов в особых случаях.
- •49 Численные методы для нахождения кратных интегралов.
- •50 Решение кратных интегралов методом ячеек
10. Модификация метода Ньютона для решения нелинейных ур-ний.
Если . f
(х)
мало изменяется в окрестности корня
,
чтобы избежать многократного вычисления
f(x),прим.модифицированный
метод Ньютона,
т.е.![]() k=0,1,2,…
(13)Геом. это означает, что к кривой f(x)
проводят касательную в точке
,
и находят пересечение x1
этой касательной с осью абсцисс. В точке
к кривой f(x)
проводят отрезок, параллельно построенной
касательной, получаем точку x2
и т.д.
k=0,1,2,…
(13)Геом. это означает, что к кривой f(x)
проводят касательную в точке
,
и находят пересечение x1
этой касательной с осью абсцисс. В точке
к кривой f(x)
проводят отрезок, параллельно построенной
касательной, получаем точку x2
и т.д.
Это позволяет уменьшить объем необходимых операций. Сходимость процесса обеспечивается при тех же условиях, что и для метода Ньютона, но при этом предъявляется меньше требований к выбору нач. приближения. Однако метод (13) обладает лишь линейной сходимостью, т.е. для него выполняется неравенство вида (14)
Достаточное условие сходимости метода (13), как и метода Ньютона можно выразить:
Если на отрезке
[a,b]
функция f(x)
является дважды непрерывно дифференцируемой
и для любой точки этого отрезка выполняется
не-во (8), т.е.
,
то метод Ньютона сходится от любой точки
.
Соотношение (8) можно записать как
(15) Если при неудачном выборе нач.
приближения
посл-сть значений f(xk)
не является
монотонно убывающей, то можно исп.
модифицированный метод Ньютона(Ньютона-Бройдена)
и определяется алгоритмом
![]() k=0,1,2,…
(16) Параметр
k=0,1,2,…
(16) Параметр
![]() - число, которое выбирается на каждой
итерации,чтобы вып-ось нер-воf(xk+1)<
f(xk)
k=0,1,2,…
(17).
- число, которое выбирается на каждой
итерации,чтобы вып-ось нер-воf(xk+1)<
f(xk)
k=0,1,2,…
(17).
при плохой сходимости
выбирают значение
![]() ,
а при хорошей сходимости
,
а при хорошей сходимости
![]() .
Если
.
Если
![]() ,
имеем метод Ньютона. Для выбора значения
параметра
используют метод половинного
деления:
,
имеем метод Ньютона. Для выбора значения
параметра
используют метод половинного
деления:
![]() .
При вычислении нер-ва (17), в котором
.
При вычислении нер-ва (17), в котором
![]() вычисляется по формуле (16) имеем
вычисляется по формуле (16) имеем
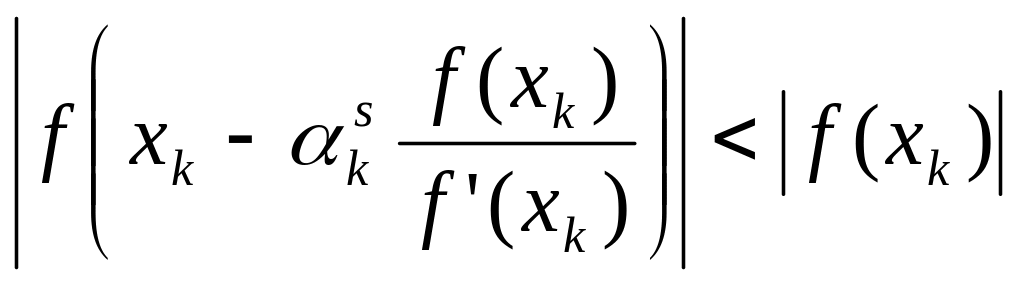
k=0,1,2,…
(18) значение параметра
![]() должно
быть таким, чтобы неравенство (18) стало
верным.
должно
быть таким, чтобы неравенство (18) стало
верным.
Определенные сложности могут возникнуть при вычислении численными методами кратных корней. Существует модификация метода Ньютона (метод Ньютона с параметром) для построения итерационной последовательности в случае корня кратности p.
![]() k=0,1,2,…
(19)
k=0,1,2,…
(19)
11. Решение нелинейных уравнений. Метод секущих
В методе Ньютона
на каждой итерации необходимо вычислять
значение функции и ее производной. На
практике применяют методы, которые
требуют вычисления на каждой итерации
только значения функции. Заменим в
методе Ньютона производную
в
точке
разделенной разностью по двум точкам
![]() ,
т.е.
,
т.е.![]() (1)
(1)
 Получаем итерационную
формулу
Получаем итерационную
формулу
![]() k=1,2,…-Формула
(2) наз.методом
секущих для
f(x)=0.
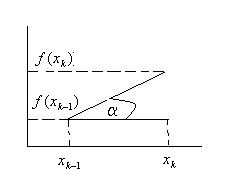
Геом. интерпретация метода состоит в
следующем. Проведем секущую через 2
точки кривой f(x)
с координатами
k=1,2,…-Формула
(2) наз.методом
секущих для
f(x)=0.
Геом. интерпретация метода состоит в
следующем. Проведем секущую через 2
точки кривой f(x)
с координатами
![]() .Пересечение
этой секущей с осью абсцисс дает
приближение
.
.Пересечение
этой секущей с осью абсцисс дает
приближение
.
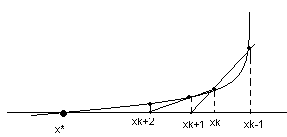
Метод секущих явл.
двухшаговым,(новое
приближение
определяется 2мя предыдущими итерациями
![]() и
).
Метод секущих сходится медленнее метода
Ньютона, вблизи корня его скорость
сходимости определяется соотнош.
и
).
Метод секущих сходится медленнее метода
Ньютона, вблизи корня его скорость
сходимости определяется соотнош.
![]() (3)
(3)
Объем вычислений на каждой итерации метода секущих гораздо меньше, т.к. не нужно вычислять значение производной. В знаменателе формулы (2) стоит разность значений функции на 2ух соседних итерациях. Вдали от корня это несущественно, но вблизи корня, особенно корня высокой кратности, значения функции малы по величине и близки между собой.Разность этих значений стремится к 0, и может возникнуть потеря значащих цифр. Это ограничивает точность, с которой можно найти корень. По этой же причине потери точности не следует приводить формулу (2) к общему знаменателю. На практике в результате потери точности возникает неустойчивость счета – осцилляции.
