
- •1.Статистика как наука
- •3. Статистическая информация и способы ее получения
- •6. Статистическая сводка, ее виды
- •7. Статистические ряды распределения
- •8. Графическое изображение статистических данных.
- •9.Статистические таблицы
- •10.Понятие о выборочном наблюдении. Виды и способы отбора
- •11. Понятия и цели в выборочном наблюдении. Ошибки выборки
- •– Стандартная ошибка.
- •12. Понятие о выборочном наблюдении. Определение необходимой численности выборки.
- •Формула степенной простой в общем виде
- •15. Структурные средние величины
Формула степенной простой в общем виде
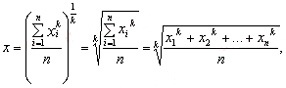
где:
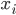 —
индивидуальное
значение признака
—
индивидуальное
значение признака
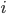 -й
единицы совокупности
-й
единицы совокупности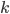 —
показатель
степени средней величины
—
показатель
степени средней величины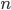 —
число
единиц совокупности
—
число
единиц совокупности
При к= -1 определенная средняя, к= 0 – ср. геометрическая, к=1 – ср. арифметическая, к=2 – ср. квадратическая, к=3 – ср. кубическая
При одних и тех же исходных данных, чем больше знач. К, тем больше значение ср. величины. Данное свойство степенных средних возрастает с повышением показателя.
15. Структурные средние величины
Кроме степенных средних в статистике для относительной характеристики величины варьирующего признака и внутреннего строения рядов распределения пользуются структурными средними, которые представлены ,в основном, модой и медианой.
Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:
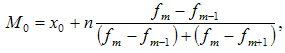
где:
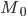 —
значение
моды
—
значение
моды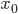 —
нижняя
граница модального интервала
—
нижняя
граница модального интервала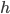 —
величина
интервала
—
величина
интервала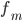 —
частота
модального интервала
—
частота
модального интервала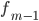 —
частота
интервала, предшествующего модальному
—
частота
интервала, предшествующего модальному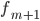 —
частота
интервала, следующего за модальным
—
частота
интервала, следующего за модальным
Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.
Для
определения медианы в дискретном ряду
при наличии частот сначала вычисляют
полусумму частот
![]() ,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле:
,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле:
Ме = (n(число признаков в совокупности) + 1)/2,
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
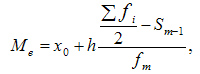
где:
 —
искомая
медиана
—
искомая
медиана— нижняя граница интервала, который содержит медиану
— величина интервала
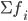 —
сумма
частот или число членов ряда
—
сумма
частот или число членов ряда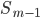 -
сумма накопленных частот интервалов,
предшествующих медианному
-
сумма накопленных частот интервалов,
предшествующих медианному— частота медианного интервала
