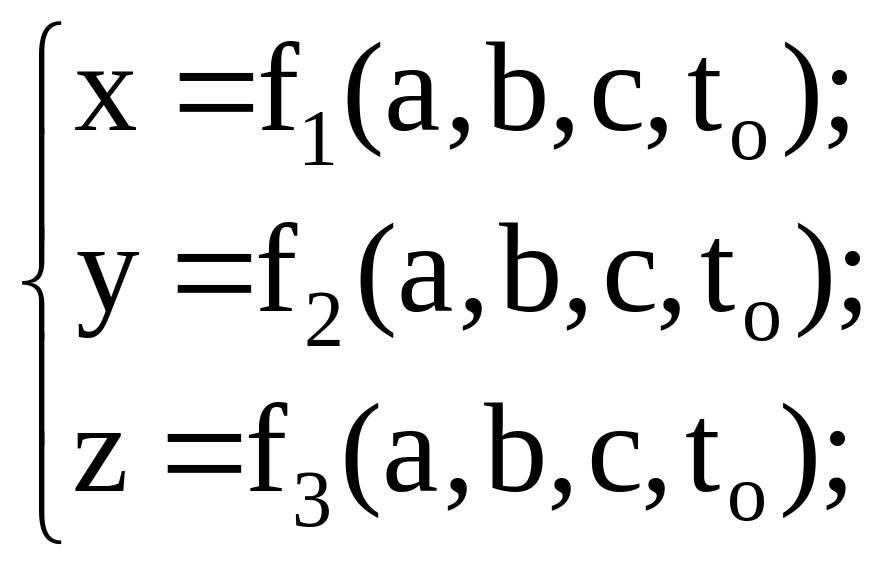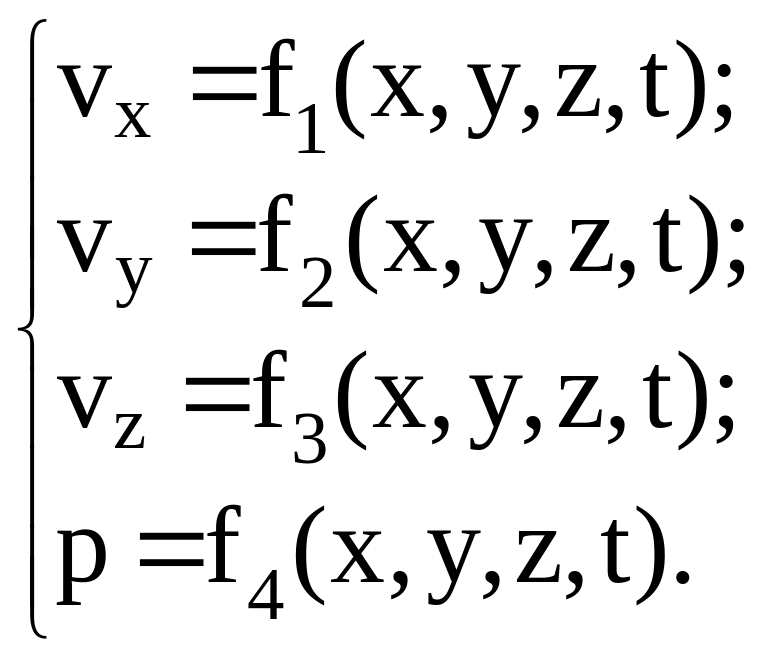1.5. Закон Архимеда

П рименим рассмотренный выше прием определения вертикальной силы давления жидкости на криволинейную стенку для доказательства закона Архимеда. Пусть в жидкость помещено тело произвольной формы (рис. 1.11) объемом V.

Спроектируем это тело на свободную поверхность жидкости и проведем проектирующую цилиндрическую поверхность, которая касается поверхности тела по замкнутой кривой. Вертикальная составляющая силы полного давления жидкости P_z1, действующая на верхнюю часть тела,

,

(1.61)

а на нижнюю часть –

.

(1.62)

Все горизонтальные силы, действующие на тело, уравновешены. Совершенно очевидно, что P_z2  P_z1, следовательно возникает выталкивающая сила

(1.63)

где V – объем тела.

Таким образом, на тело, погруженное в жидкость, действует сила, равная весу жидкости в объеме тела.

В зависимости от соотношения веса тела G и силы P_z (архимедовой силы) возможны, как известно, три варианта положения тела: GP_z – тело тонет; GP_z – всплывает; G=P_z – находится в безразличном равновесии.

2. Основы кинематики и динамики жидкости

2.1. Методы описания движения жидкостей

Гидродинамика – раздел гидравлики, в котором изучаются законы движения жидкости и применение этих законов к решению практических задач.

Существуют разные способы описания движения жидкости, из которых наибольшее распространение имеют методы Лагранжа и Эйлера.

При исследовании по методу Лагранжа изучается движение отдельных частиц жидкости вдоль их траекторий. Для выделения из бесчисленного множества траекторий частиц той, которая принадлежит данной частице, отмечают ее координаты a, b, c в начальный момент времени t_о. Координаты x, y, z и скорости v_x, v_y, v_z зависят от начальных координат:

		(2.1)
		(2.2)

По методу Эйлера определяют скорость и давление жидкости в той или иной точке пространства:

(2.3)

В гидравлике наибольшее распространение получил метод Эйлера, так как он проще метода Лагранжа.

Существует два вида движения жидкости – неустановившееся, когда скорость и давление зависят от координат и времени, и установившееся, когда указанные параметры не зависят от времени.

В дальнейшем будем рассматривать только установившееся движение жидкости. Установившееся движение, при котором частицы жидкости сохраняют свою скорость одинаковой по длине потока, называется равномерным.

На практике встречаются следующие виды потоков – напорные, безнапорные, струи. В напорных потоках все поперечное сечение трубы, канала заполнено жидкостью, движение которой осуществляется под напором, создаваемым тем или иным источником энергии.

Безнапорные потоки имеют свободную поверхность. Такое движение осуществляется в каналах, руслах рек, трубопроводах, работающих неполным сечением за счет сил тяжести.

Струи – это потоки, имеющие свободную поверхность по всему периметру сечения, движение здесь осуществляется за счет сил инерции.