1.3. Дифференциальные уравнения Эйлера и их интегралы. Основное уравнение гидростатики

О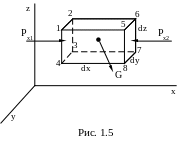 пыт показывает, что гидростатическое давление в разных точках объема разное, т. е. p = f(x, y, z). Установим эту функциональную связь. С этой целью выделим внутри покоящейся жидкости элементарный параллелепипед с ребрами dx, dy, dz (рис. 1.5). Мысленно отбросим окружающую жидкость и заменим ее воздействие на параллелепипед силами. Спроектируем силы на ось Х. Так как параллелепипед находится в равновесии, то

Рx1 – Px2 + Gx = 0.

(1.16)

Предположим, что гидростатическое давление, действующее на грань 1234, равно p, а грань находится на расстоянии х от начала координат. Тогда

.

(1.17)

В связи с тем, что координата грани 5678 равна х + dx, а р = f(x, y, z), давление, действующее на эту грань, будет и

(1.18)

Проекцию массовых сил на ось Х представим так:

.

(1.19)

Здесь Х – проекция ускорения массовых сил на ось х. Подставляем указанные силы в уравнение (1.16):

(1.20)

Раскроем скобки в уравнении (1.20) и получим:

(1.21)

После очевидных преобразований получим:

(1.22)

Произведя аналогичные преобразования для осей Y и Z, получим систему дифференциальных уравнений Эйлера:

; ; .

(1.23)

Каждое из уравнений системы (1.23) представляет собой закон распределения давления вдоль соответствующей оси координат. Совокупность двух любых уравнений выражает закон распределения гидростатического давления в соответствующей плоскости, а трех – закон распределения гидростатического давления в объеме жидкости.

Заменим систему уравнений (1.23) одним уравнением. С этой целью умножим каждое уравнение на dx, dy, dz соответственно и произведем почленное сложение, тогда

(1.24)

Так как гидростатическое давление является функцией координат, выражение в правой части уравнения (1.24) является полным дифференциалом давления dр, следовательно,

(1.25)

Уравнение (1.25) является основным уравнением гидростатики в дифференциальной форме.

Рассмотрим случай, когда на жидкость действуют только силы тяжести.

Тогда X = 0, Y = 0, Z =  g и уравнение (1.25) примет вид:

(1.26)

или

.

(1.27)

Проинтегрируем уравнение (1.27) и получим:

,

(1.28)

где С – постоянная интегрирования;

z – геометрическая высота, м;

– пьезометрический напор, м.

П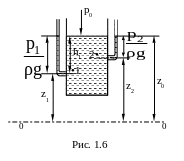 остоянную интегрирования найдем, подставив в уравнение (1.28) параметры свободной поверхности (рис. 1.6) z = z₀, p = p₀, тогда,

(1.29)

Тогда

(1.30)

и ли

(1.31)

Обозначим (z₀ – z) = h, тогда

(1.32)

Полученное выражение (1.32) называется основным уравнением гидростатики, которое позволяет рассчитывать давление в любой точке объема жидкости.
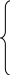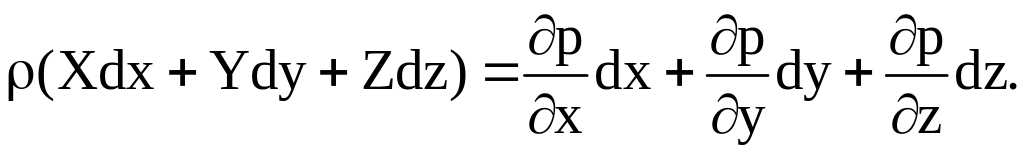
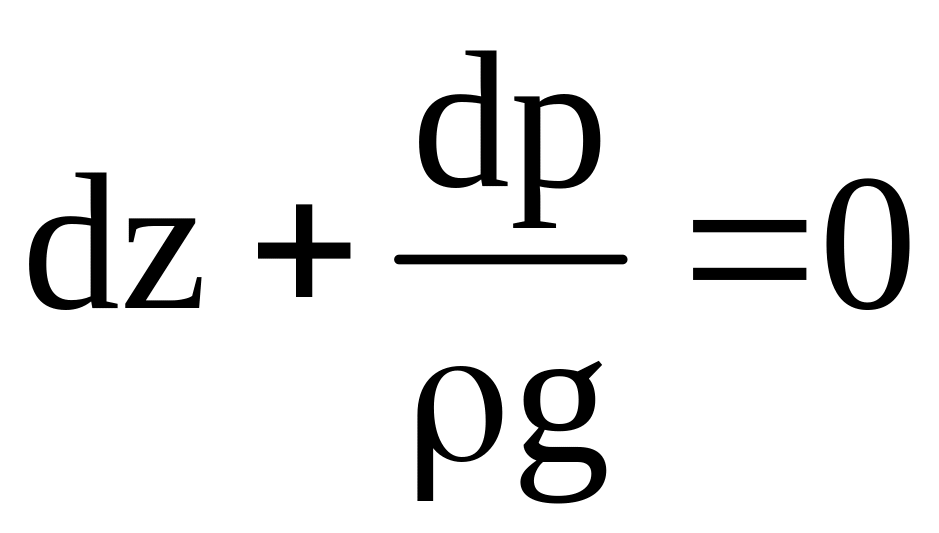