3.2. Понятие о гидродинамическом подобии

Сложность процессов, протекающих в жидкости не позволяет в полной мере использовать результаты теоретического анализа для решения практических задач, поэтому в гидравлике широко используется эксперимент в сочетании с теорией. Очевидно, что при постановке эксперимента возникает нужда в исследовании не натурных образцов гидравлических сооружений и устройств, а мо­делей этих устройств. При создании и исследовании моделей воз­никают такие вопросы: какие явления и процессы подобны изучаемому; что измерять при проведении эксперимента; как обрабаты­вать результаты исследования. Ответы на эти и другие вопросы дает наука о постановке эксперимента – теория подобия.

Подобными явлениями называются явления качественно одина­ковые, описываемые одинаковыми дифференциальными уравнениями. Гидродинамическое подобие – это подобие геометрическое, кинема­тическое и динамическое.

Геометрическое подобие означает пропорциональность сходст­венных размеров и равенство соответствующих углов: ; ; .

Кинематическое подобие – это подобие линий тока и пропорциональность сходственных скоростей, ускорений: ; ; .

Динамическое подобие – это подобие масс, плотностей, сил: ; ; .

Здесь индексы Н относятся к натурному потоку, М – к мо­дельному, соответственно L – линейный размер; F – площадь; W – объем; v – скорость; t – время; a – ускорение; m – масса;  – плотность;  – динамический коэффи­циент вязкости; Р – сила; С – масштаб моделирования.

Получим основной критерий гидродинамического подобия. В соответствии с законом Ньютона Р = m а. Для подобных потоков

(3.3)

или

.

(3.4)

Имея в виду значения масштабов моделирования, можно записать:

.

(3.5)

Поскольку комплексы (3.5) для подобных потоков должны быть одинаковыми, запишем:

.

(3.6)

Чаще пользуются другим выражением. Так как t = L/v, то

.

(3.7)

Полученный комплекс (3.7) называется критерием Ньютона.

Согласно первой теореме теории подобия подобные между собой явления имеют одинаковые критерии: Ne_н = Ne_м .

Вторая теорема подобия утверждает, что интеграл дифферен­циального уравнения, описывающего процесс движения жидкости, может быть представлен в виде зависимости между критериями подобия: f (k₁, k₂, k₃ …) = 0.

Если результаты опыта представить в критериальной форме, то эти критериальные зависимости будут общими для всех подоб­ных явлений.

Для получения общего гидродинамического подобия необходимо иметь подобие по всем силам, действующим в системе. Однако это не всегда возможно. В таких случаях пользуются частичным (локальным) подобием по силам, преобладающим в изучаемом пото­ке. При этом критерий Ne преобразуется в другие критерии.

Пусть в потоке преобладают силы трения. Тогда в соответ­ствии с законом

Ньютона

.

(3.8)

Подставим в критерий Ньютона вместо Р силу трения Т и получим:

.

(3.9)

В подобных системах , поэтому

(3.10)

или

.

(3.11)

Запишем выражение (3.11) через масштабы моделирования:

.

(3.12)

Помня о том, что С_ /С_ = С_, уравнение (3.12) примет вид:

.

(3.13)

Следовательно,

.

(3.14)

Комплекс (3.14) назван критерием Рейнольдса и для подобных потоков, в которых главную роль играют силы трения

.

(3.15)

Для круглой трубы характерным линейным размером является диаметр d и

.

(3.16)

Если в потоке преобладают силы тяжести, то в качестве силы Р в критерий Ньютона следует подставить G = mg:

.

(3.17)

После очевидных сокращений получим:

.

(3.18)

Отношение, обратное уравнению (3.18), называется критерием Фруда:

.

(3.19)

Следовательно, в тех случаях, когда моделируются явления, при которых преобладают силы тяжести, должно соблюдаться равенство критериев Фруда натуры и модели.

Если в жидкости преобладают силы давления, то в критерий Ньютона подставляют Р=рF. После несложных преобразований получают критерий Эйлера

.

(3.20)

В подобных потоках требуется равенство критериев Эйлера для натуры и модели: Eu_н = Eu_м.

С физической точки зрения все полученные критерии представляют собой меру отношения сил инерции к преобладающим в потоке жидкости силам.

Современная теория подобия рекомендует все результаты экспериментов представлять в виде критериальной зависимости: Еu = f (Re, Fr).

Покажем, что коэффициент сопротивления  в формуле для расчета потерь напора по длине тоже является критерием подобия. Докажем это положение. Так как , то после несложных преобразований получим:

,

(3.21)

или

.

(3.22)

Ниже убедимся в том, что  = f (Re), и тогда получим, что

,

(3.23)

а это согласуется с требованиями теории подобия.
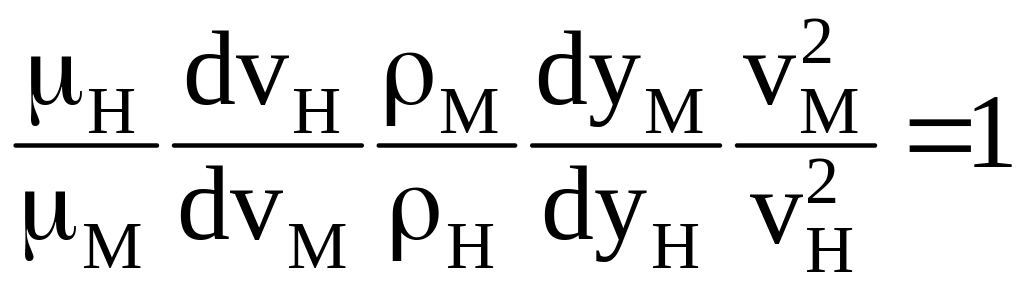