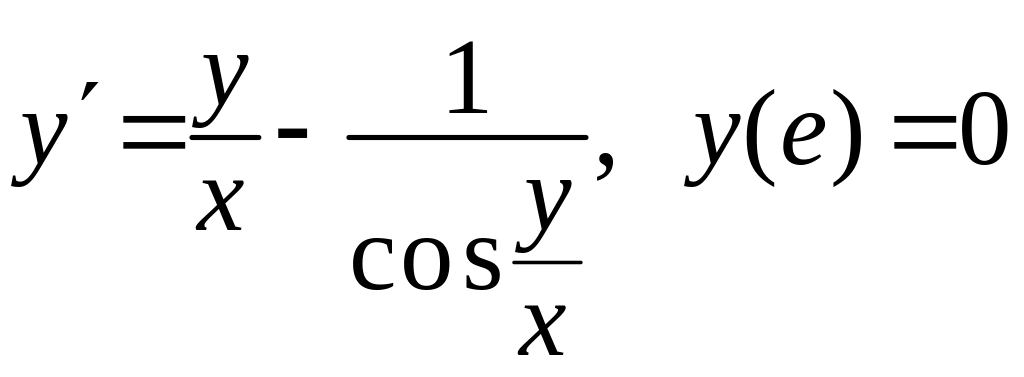кандидат технических наук, доцент А.Е. Есипова
кандидат физико-математических наук, доцент И.Н. Нурутдинова
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ: Метод. указания и варианты заданий к контрольным работам по дисциплине «Математика». В 2 ч. Ч. 1 / РГАСХМ ГОУ, Ростов н/Д, 2008.
Введение
Методические указания предназначены для студентов 2-го курса заочной формы обучения всех специальностей и содержат варианты заданий контрольной работы № 5 по теме: «Дифференциальные уравнения». Приведены краткие теоретические сведения и примеры выполнения заданий.
Перед началом выполнения контрольной работы необходимо изучить теоретический материал, используя методические указания, конспекты установочных занятий и рекомендуемую литературу.
Контрольная работа оформляется в отдельной тетради, регистрируется в деканате и передается на проверку преподавателю в установленные сроки.
1. Варианты заданий контрольной работы № 5
Номер варианта |
Задание 1.1. Найти общее решение ДУ 1-го порядка с разделяющимися переменными |
Задание 1.2. Найти общее решение однородного ДУ 1-го порядка |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
Номер варианта |
Задание 1.3. Найти общее решение линейного ДУ 1-го порядка |
Задание 1.4. Найти общее решение уравнения Бернулли |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
Номер варианта |
Задание 1.5. Определить тип ДУ 1-го порядка и решить задачу Коши |
Задание 2.1. Решить задачу Коши для ДУ второго порядка |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
Номер варианта |
Задание 2.2. Найти общее решение линейных однородных ДУ 2-го порядка с постоянными коэффициентами |
|||
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
Номер варианта |
Задание 2.3. Найти общее решение линейного неоднородного ДУ 2-го порядка с постоянными коэффициентами |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
