
- •3. Визначники 2–го порядку та їх властивості.
- •6. Означення визначника n-го порядку
- •7. Властивості визначників n-го порядку
- •8. Поняття вектора.Лінійні дії над векторами.
- •9. Лінійно незалежні системи векторів. Базис, розклад вектора за базисом.
- •10. Проекція вектора на вісь.
- •11 Декартова система координат. Координатна форма вектора.
- •12.Скалярний добуток векторів
- •13 Векторний добуток векторів
- •14. Мішаний добуток трьох векторів.
- •15. Векторне і нормальне рівняння площини.
- •16. Загальне рівняння площини. Відстань та відхилення точки від площини.
- •17. Кут між двома площинами.
- •20. Кут між пр в прост. Умови належн двох прямих одній площині
- •21. Взаємне розташув 2 площ. Кут між прямою і площиною
- •22. Канонічне рівняння еліпса, його геометричні властивості.
- •25. Загальне рівняння кривої другого порядку.
- •26. Види матриць. Лінійні операції над матрицями.
- •27 Множення матриць
- •28 Елементарні перетворення матриць
- •32. Компл числа. Тригонометрична форма комплексного числа
- •33. Дії над компл. Числами. Ф-ла Муавра
- •34. Операції над многочленами. Нсд
25. Загальне рівняння кривої другого порядку.
Крив 2 порядку назив. множ точок площ, що задовольняють р-ня
 З’ясуємо,
що являє собою крива 2-го порядку
геометрично. Для цього спочатку повернемо
систему координат
З’ясуємо,
що являє собою крива 2-го порядку
геометрично. Для цього спочатку повернемо
систему координат
 на кут
проти годинникової стрілки так, щоб у
рівнянні зник добуток
на кут
проти годинникової стрілки так, щоб у
рівнянні зник добуток
 .
.


Випишемо
коефіцієнти при
 в
рівнянні кривої
в
рівнянні кривої

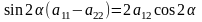
Якщо
 Якщо
Якщо


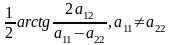

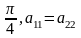
Вважаємо, що поворот с-ми коорд відбувся, тоді р-ня кривої:
 Розглянемо
такі випадки:
Розглянемо
такі випадки:
1 .
.
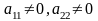 Зробимо заміну змінних
Зробимо заміну змінних
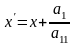

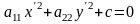
а)
 одного знаку протилежного С, тоді ця
крива еліпс.
одного знаку протилежного С, тоді ця
крива еліпс.
б)
 протилежних знаків, тоді на виході крива
гіпербола.
протилежних знаків, тоді на виході крива
гіпербола.
в)
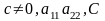 одного знаку уявна
крива
одного знаку уявна
крива
г)
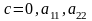 різних знаків – дві прямі, що перетинаються
різних знаків – дві прямі, що перетинаються
д)
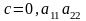 одного знаку – дійсна точка
одного знаку – дійсна точка
2 .
Нехай
.
Нехай
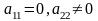

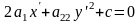
а)
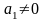 - парабола б)
- парабола б)
 - різн знаків, пара парал пр в)
- одн знаку, пара уяв пр г)
- різн знаків, пара парал пр в)
- одн знаку, пара уяв пр г)
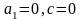 - пара пр, що збіг
- пара пр, що збіг
26. Види матриць. Лінійні операції над матрицями.
Матрицею
А розмірів
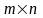 назив. сукуп чисел (елем матриці) розміщ
у вигляді прямокутної таблиці, яка має
m-рядків
і n-стовпців
назив. сукуп чисел (елем матриці) розміщ
у вигляді прямокутної таблиці, яка має
m-рядків
і n-стовпців

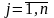
Мат А і В назив. рівними,якщо вони мають одн розм і їх відп елем рівні
Види матриць
1) Матриця, всі елементи якої рівні нулю назив. нульовою (θ)
2) матриця назив. квадр порядку n, якщо m=n. (інша-прямокутна)
3) М, що скл з одного стовпця (рядка) назив. матрицею-стовп (-ряд). Ці матриці також назив векторами.
4)
М
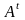 розм
назив. транспон до М А, розмірів
,
якщо
одерж з А перетвор стовпців у рядки з
тим самим номером
розм
назив. транспон до М А, розмірів
,
якщо
одерж з А перетвор стовпців у рядки з
тим самим номером
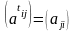
5)
М А назив. симетрич (кососиметричною),
якщо

6)
Діагонал елем М А назив. його ел
 ,
решта ел назив. позадіаг. Квадратна М А
назив. діаг, якщо всі її позадіаг ел
дорівнюють нулю.
,
решта ел назив. позадіаг. Квадратна М А
назив. діаг, якщо всі її позадіаг ел
дорівнюють нулю.
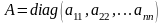
Якщо всі діагональні ел рівні між собою, то така матр назив. скалярною. Якщо у такої матриці всі діаг ел дорівнюють 1, вона назив. одиничною.
( )
)
7) Якщо всі ел матриці розміщ нижче(вище)гол діаг = 0, то така М назив. верхньою(нижньою) трикут.
8)
Квадратна М А назив. невиродж (виродж),
якщо
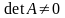 (det
A=0)
(det
A=0)
Лінійні операції
Сумою
матриць А і В однак розмірів назив. матр
А+В тих же розм ел якої дорівн сумам
відпов ел матриць А і В.
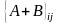 - ij-ий
ел М А+В
- ij-ий
ел М А+В
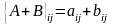
Добутком
матриці А на число
назив. М
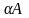 тих самих розмірів, що і А, ел якої є
добутк відпов ел А на число
тих самих розмірів, що і А, ел якої є
добутк відпов ел А на число

Властивості лінійних операцій над матрицями
1) 1 А=А 1=А
2) 0 А=А 0 = 0(нуль-матриця)
3)
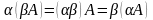
4) А+В=В+А (комутативність)
5)
А+(В+С)=(А+В)+С 6)
 (дистрибутивність)
(дистрибутивність)
7)
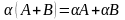 8) А+О=А 9)
8) А+О=А 9)
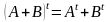
10)

27 Множення матриць
Добутк матриці А (розмірів mхk) на матр В (kхn) називається матриця АВ розмірів m на n, елементи якої дорівнюють сумі добутків відповідних елементів і-го рядка А і j-го стовпця В. {AB}ij=∑ks=1ais*bsj (1)
Множ матр можливе лише тоді, коли к-сть стовбців А = к-сті рядків В.
Властивості добутку матриць
1) α(АВ)=( αА)В=А(αВ)
2) (А+В)С=АС+ВС
3) А(В+С)=АВ+АС
4) (АВ)С=А(ВС)
5) (АВ)т=ВтАт
Доведення
Властивості 1-3 очевидні
{(AB)C}ij A m*n, B p*k, C k*n
{(AB)C}ij=∑kl=1 (∑ps=1aisbsl)clj
{(AB)C}ij=∑ps=1ais(∑kl=1bsl clj) Одерж суми відрізн лише порядком доданків. Отже маємо рівність відпов ел
{(AB)т}ij={AB}ij=∑ks=1ajsbsi=∑ks=1{Aт}sj{Bт}is=∑ks=1{Bт}is{Aт}sj={Bт Aт }ij
У загал випадку АВ≠ВА навіть можливо, що ВА – не існує .
Введемо поняття лінійної комбінації стовбців і рядків А. Позначимо і-тий рядок А аі.=(аі1,ai2,...,ain) a.j=(a1j,a2j,...,amj)т
Лін комбінацією рядків матриці А називається сума ∑mi=1αiai. , де αi – дійсні, і=1,m
Лін комбінацією стовбців матриці А називається сума ∑nj=1 βja.j , де βj є R, j=1,n
Перепишемо формулу (1) у 2 випадках
{AB}.j=∑ks=1a.sbsj (2) {AB}i.=∑ks=1aisbs. (3)
Ф-ла (2) показує, що будь-який j-тий стовбець є лінійною комбінацією стовбців А при чому коефіцієнти утворюють j-тий стовбець В.
З (3) випливає, що і-тий рядок В є лінійною комбінацією рядків В. Коефіцієнти лінійної комбінації є елементами і-того рядка А. Отже, якщо треба працювати зі стовбцями (рядками) матриці то треба помножувати матрицю на відповідні матриці справа(зліва).
