8. Поняття вектора.Лінійні дії над векторами.

Вектор-направл відрізок AB, де А- початок, B- кінцева точка вектора.

Нуль-вектор(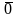 )-вектор у якого початок і кінець збігаються.

Будьякий вектор хар-ться напрямком і довжиною(модулем)

Нуль вектор: | |=0,напрям-невизначений.

Колінеар вектори 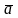і , якщо лежать на одній, або паралельних прямих

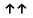-колінеарні співнапрямлені

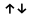- колінеарні протилежно напрямлені

Вектори і називаються рівними, якщо:

1. | |=| | 2)

Зауваження: рівний , можна одержати з паралельним перенесенням Вектор є вільним відносно точки прикладення.

Лінійні Операції над векторами

1. | |=| |*| |

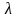2. , >0 , <0

3. = =0 або =

Вектор - називається протилежним , якщо - =(-1)

Зауваження:колінеарність || =

Якщо , то | | 0.

Ортом вект а наз одинич вект, що має той самий напрям, що і а:

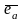, | |=1 тоді =| |*

Властивості добутку вектора на скаляр

1. 1* = 2)( ) = ( )

Сумою Векторів і називаеться вектор = + ,який визначається за правилом трикутника , або паралелограма.

Властивості суми векторів:

1.комутативність: + = +

2.асоціативність: + + = ( + )+

3.дистрибутивність ( + )= + * = +

4. + = +(- )=

9. Лінійно незалежні системи векторів. Базис, розклад вектора за базисом.

Лін комб вект 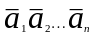назив вектор

=

Вектори 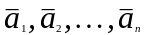лін-залежн, якщо існ скаляри всі не =0, такі що лін. комбінація векторів =

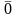
Векторів —лін-незалежн, якщо рівність можлива лише тоді, коли всі =0

Властивості лін.-залежних і лін.-незалежних векторів:

Террема 1 Якщо сист. векторів лін.-залежна, то принаймні 1 з векторів с-ми є лін. комб інших.

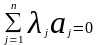
Довед: Нехай лін.-залежна,тоді є R., тоді . це лін. комб вект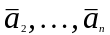

Теорема 2 Якщо сист. векторів лін.- незалежна, то вона не містить , та жоден вектор системи не є лін. комб. інших векторів системи.

Доведення:а) нехай - лун. незалежні. , , 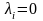i=1,n; . Отже, сист. лін.-залежна, що суперечить умові.

б) припустимо, що якийсь 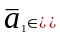лін. комбінацією інших векторів. ;

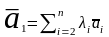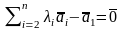
Коеф при а1=-1, алін комб 0, отже система векторів лін залежна, що суперечить умові.

Вектори компланарні, якщо лежать в 1 або парал площинах. ТЕОРЕМА:В множині всіх компл векторів будь-які 2 ненул неколінеарні вектори є лінійно-незалеж, а будь-який 3-й вектор є лін. комбін цих векторів.

Доведення: Нехай 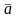не ||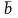 , . Доведемо, що і лін.-незалежні. Нехай і лін.-залежні, тоді а це суперечить умові. Отже, і лін- незалежні.

Розгл. 3 вектори , і , зведені в 1 точці.

Через кінець проведемо прямі паралельно і . =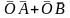 . В силу колінеарності відповідних векторів, маємо 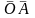= , 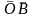= 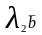. Тоді = + . Отже, є лін комб. і . Зауважимо, що розклад за і є однознач.(Довед: нехай є друг вектор 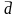= + 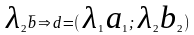)коорд. вектора , тобто ці в-ри є рівними=> співпад з . Ми дійшли до суперчн, -єдин.

Множина всіх компл в-рів з визнач оперціями додав векторів та множ на скаляр є прикладом векторного прост.

Найбіл к-сть лін-незал вект простору назив. його розмірністю, а сама система лін-незал векторів назив. базисом простору.

Множина всіх компл вкторів є вект прост розмірності 2 і познач. . Базис склад з буд-як 2 неколін векторів.

ТЕОРЕМА:в множині всіх векторів геом. простору будь-які 3 некомпланарні вектори є лінійно-незал, а будь-який 4-й вектор є лін. комб цих векторів. Множина векторів геом. Простору є 3-вимірною і позн .