17.Движение в неинерциальных системах отсчета. Кинематика относительного движения.Абсолютные,Относительные,переносные скорости и ускорения, кориолисово ускорение.

Неинерциа́льная систе́ма отсчёта — система отсчёта, к которой не применим закон инерции (говорящий о том, что каждое тело, в отсутствие действующих на него сил, движется по прямой и с постоянной скоростью), и поэтому для согласования сил и ускорений в которой приходится вводить фиктивные силы инерции. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, является неинерциальной.Законы Ньютона выполняются только в инерциальных системах отсчёта.

Во многих случаях необходимо изучать движение материальной точки или тела по отношению к неинерциальной системе отсчета. Рассмотрим движение материальной точки М относительно двух прямо­угольных декартовых систем координат X, Y, Z и X', Y', Z' (рис. 7.1). Пусть первая система координат является инерциальной, а вторая движется относи­тельно нее произвольным образом. Систему X, Y, Z будем условно считать неподвижной.а движение точки М относительно этой системы отсчета будем называть абсолютным движением. Движение точки М относительно подвижной системы отсчета X', Y', Z' будем называть относительным движением. Положение точки М относительно неподвижной системы координат определяется радиусом-вектором г = х\ + yj + zk, а относительно подвиж­ной — радиусом-вектором г' =x'i' + у'j' + г'к', где х, у, г и х', у', г' — коор­динаты точки М в этих системах. Из рис. видно, что

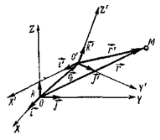
r=r0+r’=r0+ x'i' + у'j' + г'к'(1)

где г0 — радиус-вектор, проведенный из начала О неподвижной системы в начало О' подвижной системы координат.

Скорость точки М относительно неподвижной системы координат равна

и называется абсолютной скоростью точки

Из (1) следует, что (2’) ИЛИ (3)

где (4)-абсолютная скорость точки О', т. е. скорость подвижной системы координат в ее поступательном движении. Вектор по аналогии с (2) определяет скорость точки М относительно подвижной си­стемы координат. Его называют относительной скоростью точки М.Изменение ортов i', j' и к' подвижной системы координат может быть вызва­но лишь тем, что эта система движется не только поступательно, но одиовременно вращается вокруг точки О', Следовательно, векторы и являются линейными скоростями концов соответствующих ортов в этом вращатель­ном движении. Если угловая скорость подвижной системы равна ,то (6),а (7)

На основании соотношений (4), (5) и (7) уравнение (3) можно теперь переписать в таком виде:

(8)

Сумма первых двух членов правой части второго равенства представляет собой абсолютную скорость той точки подвижной системы (т.е.жестко связанной со всей сист.),через которую в данный момент времени проходит рассматриваемая матер. т.М. Эту скорость называют переносной скоростью точки М и обозначают _е.

(9)

Т аким образом, абсолютная скорость точки М равна сумме ее переносной и относительной скоростей:

(10)

Абсолютным ускорением точки М называют ее ускорение по отношению к неподвижной инерциальной системе отсчета:

Из уравнений (10) и (9) следует, что

или на основании (5) и (6):

(11)

где (12)

ускорение подвижной системы в ее поступательном движении, (13)

угловое ускорение подвижной системы, (14)

о тносительное ускорение точки М (ее ускорение по отношению к подвижной системе). Из сопоставления формул (2'), (4) и (8) видно, что

Поэтому уравнение (11) можно записать в такой форме: (15)

или (16) где (17)

• переносное ускорение точки М, равное абсолютному ускорению той точки подвижной системы, через которую в данный момеит времени проходит рассмат­риваемая материальная точка М;

(18)

►—кориолисово, или поворотное, ускорение точки М, обусловленное враще­нием подвижной системы.

Таким образом, равенство (16) свидетельствует о том, что абсолютное ус­корение точки равно сумме ее переносного, кориолисова и относительного уско­рений.

Как видно из (18), кориолисово ускорение максимально, если относитель­ная скорость точки _r перпендикулярна к вектору  угловой скорости подвиж­ной системы. Если угол между векторами _r и  равен 0 или , то кориолисово ускорение равно нулю

Если подвижная система так же, как и неподвижная, является инерциальиой, то==a₀=0, и уравнения (10) и (16) переходят в известные соотношения:

v = v₀ + v_r и

вытекающие из преобразований Галилея

В том случае, когда подвижная система движется только поступательно(==0), уравнения (10) и (16) имеют следующий вид:

v = v₀ + v_r и

Теорема о сложении ускорений (теорема Кориолиса):  , где   – ускорение Кориолиса (кориолисово ускорение) – в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки из-за ее относительного движения; 2) изменение направления относительной скорости точки из-за вращательного переносного движения. Модуль ускорения Кориолиса: а _с=2×|_e×v_r|×sin(_e^{^}v_r), направление вектора  определяется по правилу векторного произведения, или по правилу Жуковского: проекцию относительной скорости на плоскость, перпендикулярную переносной угловой скорости, надо повернуть на 90^о в направлении вращения.

Кориолисово уск. = 0 в трех случаях: 1) w_e=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0; 2) v_r=0; 3) sin(w_e^{^}v_r)=0, т.е. Ð(w_e^{^}v_r)=0, когда относительная скорость v_r параллельна оси переносного вращения. В случае движения в одной плоскости – угол между v_r и вектором _e = 90^о, sin90^o=1, а_с=2×_e×v_r.