
- •1. Кинематика материальной точки.
- •2. Скорость и ускорение
- •3. Криволинейное движение тела
- •4. Динамика материальной точки. Законы Ньютона
- •5. Импульс тела
- •6. Импульс системы материальных точек.
- •8. Кинетическая и потенциальная энергия. Механическая энергия. Консервативные силы.
- •9. Закон сохранения механической энергии
- •10. Связь консервативной силы с потенциальной энергией
- •11. Центральный удар шаров. Абсолютно упругий удар.
- •12. Центральный удар шаров. Абсолютно неупругий удар. Частично неупругий удар. Коэффициент восстановления относительной скорости при ударе.
- •13. Кинематика вращательного движения. Угловая скорость, угловое ускорение. Связь с линейными величинами: линейной скоростью, тангенциальным(касательным) ускорением и нормальным ускорением.
- •14. Динамика вращательного движения. Момент силы. Момент инерции. Основное уравнение динамики вращательного движения.
- •15. Момент импульса. Закон сохранения момента импульса.
- •16.Кинетическая энергия вращающегося тела.
- •17.Движение в неинерциальных системах отсчета. Кинематика относительного движения.Абсолютные,Относительные,переносные скорости и ускорения, кориолисово ускорение.
- •18. Движение в неинерциальных системах отсчета. Динамика относительного движения. Основное уравнение деинаики относительного движения материальной точки.
- •19. Преобразование Галилея. Экспериментальные факты подтверждающие, теорию относительности.
- •20. Постулаты Эйнштейна. Преобразования Лоренца
- •Следствия из преобразований Лоренца
- •24. Релятивистский импульс
- •25. Релятивистское выражение для энергии.
- •26. Работа и теплота
- •27. Теплоёмкость идеального газа.Теплоёмкость при постоянном объёме и постоянном давлении.Уравнение Майера.
- •28. Теплоёмкости одноатомных и многоатомных газов
- •30. Изоэнтропийный процесс
- •31. Изотермический процесс
- •32. Обратимые и необратимые процессы.Энтропия.
- •33. Второе начало термодинамики.
- •34. Цикл Карно.
- •35.Основное уравнение кинетической теории газов.
- •37. Барометрическая формула. Распределение Больцмана.
- •38. Средняя длина свободного пробега молекул.
- •39. Явления переноса в газах. Диффузия.
- •40. Явление переноса. Элементарная теория диффузии.
- •41. Явления переноса. Теплопроводность газов.
- •42. Явления переноса. Вязкость газа.
- •43. Механические колебания. Свободные гармонические колебания.
- •44. Свободные затухающие колебания.
- •45. Вынужденные механические колебания.
- •46. Явление механического резонанса.
9. Закон сохранения механической энергии
Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
Классическим примером этого утверждения являются пружинный или математический маятники с пренебрежимо малым затуханием. В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно. В случае математического маятника аналогично ведёт себя потенциальная энергия груза в поле силы тяжести.
Сумма кинетической и потенциальной энергий системы тел называется полной механической энергией системы.
E = Ep + Ek
Учитывая, что при совершении работы A = DEk и, одновременно, A = - DEp, получим: DEk = - DEp или D(Ek + Ep)=0 - изменение суммы кинетической и потенциальной энергий (т.е. изменение полной механической энергии) системы равно нулю.
DEk = - DEp
Значит, полная энергия системы остается постоянной:
E = Ep + Ek = const.
В замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется. (Или: полная механическая энергия системы тел, взаимодействующих силами упругости и гравитации, остается неизменной при любых взаимодействиях внутри этой системы).
E = Ep + Ek = const
Например, для тела, движущегося под действием силы тяжести (падение; тело, брошенное под углом к горизонту, вертикально вверх или движущееся по наклонной плоскости без трения).
10. Связь консервативной силы с потенциальной энергией
dWp=-
dWp (x, y, z)
dWp=(δWp/δx)dx+(δWp/δy)dy+(δWp/δz)dz
=Fxdx+ Fydy+ Fzdz
=Fx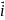 +
Fy
+
Fy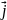 +
Fz
+
Fz
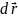 =dx
+
dy
+
dz
=dx
+
dy
+
dz
Fxdx+ Fydy+ Fzdz=-(δWp/δx)dx-(δWp/δy)dy-(δWp/δz)dz
x= Fx =-(δWp/δx)
y= Fy =-(δWp/δy)
z= Fz =-(δWp/δz)
∆Wp=-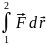 →
Wp2-Wp1=-
→
Wp2-Wp1=-
11. Центральный удар шаров. Абсолютно упругий удар.
Удар — толчок, кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер. В физике под ударом понимают такой тип взаимодействия движущихся тел, при котором временем взаимодействия можно пренебречь.
Центральным ударом называется такое взаимодействие тел, когда их скорости направлены вдоль линии, соединяющей их центры.
Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. Математическая модель абсолютно упругого удара работает примерно следующим образом:
1. Есть в наличии два абсолютно твердых тела, которые сталкиваются
2. В точке контакта происходят упругие деформации. Кинетическая энергия движущихся тел мгновенно переходит в энергию деформации.
3. В следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации вновь переходит в кинетическую энергию.
4. Контакт тел прекращается и они продолжают движение.
