6. Импульс системы материальных точек.

Любое реальное тело в ряде случаев бывает удобно рассматр. как сист. мт. В этом случае тело разбивают на малые эл-ты или малые части, такие, что кажд. такую часть можно считать мт. Учитывается взаимодействие мт, образующих сист., между собой и внешними телами и полями. С этой целью задаются силы, действ. на мт сист. Рассматривая движение такой сист. мт можно сделать вывод о движении тел.

F_i – результирующая внешних сил, действующих на i мт.

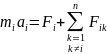
a_i=dV_i/dt

Сложим все уравнения, к-рые описывают движение мт.

Если проанализировать последнюю сумму, то

F_ik=-F_ik

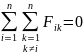
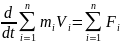
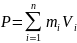
импульс системы

Закон изменения импульса системы

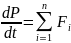
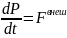
Пусть на нашу систему не действуют внешние тела и поля, тогда главный вектор внешних сил будет равен 0.

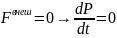
P=const

Импульс нормированной сист. тел есть величина постоянная. Под изолированной сист. понимается сист. тел, на к-рые действ. внешн. тела и поля.

7. Механическая работа. Работа переменной силы.

Энергия – это скалярная величина, к-рая явл-ся единой количеств. мерой различн. форм движ-я материи и соотв. этим формам взаимод-я.

Механическое движ-е. Такого рода движ-е принято характериз. механич. эн-ей, к-рая выст. в кач-ве колич. меры механич. движ-я рассматр. сист., а также мерой механич. взаимод-я тел др. с др. и с внешн. телам и полями.

Механическая работа, работа силы. Измен-е механич. движ-я происх.в процессе механич. действия на рассматр. тело со стороны других тел. Говоря об изменении механич. движ-я можем говорить об изменении механич. энергии.

Мерой механич. воздействия явл-ся сила изменения мех. движ-я происходящего под действием сил.

Для того, чтобы описывать изменение мех. эн-ии придется ввести понятие работы.

При перемещении тела под д-ем силы F будет соверш. мех. раб.

∆A= ∆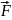

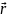
∆ = F∆rcosα

Fcosα=F_τ

∆A= F_τ∆r

Если F окаж. перп. направл-ю, то такая F работы совершать не будет.

Работа переменной силы.

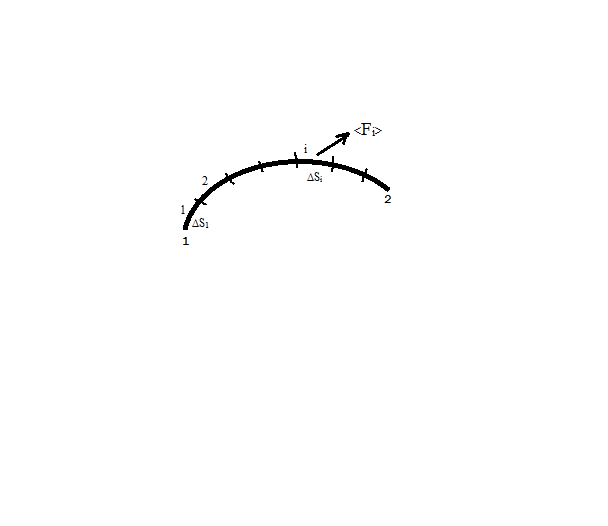
Если участки, на к-рые разб. траектория, малы, то движ-е должно рассматр. как движ-е по прямой под действием постоянной силы.

Работу можно найти как сумму работ.

∆A_i=< >∆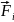

∆ ≈∆S_i> (d =dS )

∆A_i=<F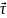_i> ∆S_i

<F_ri>=< _i> =< _i>cos(< _i>^, )

∆A_i=< _i>∆ =< _i>τ∆S_i=<F_τi>∆S_i

∆A_i=<F_τi>∆S_i

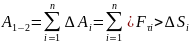
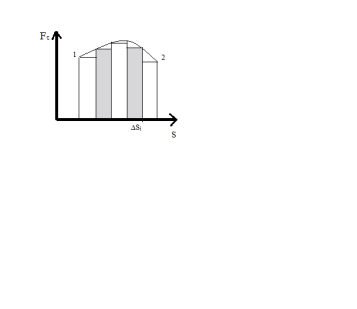
Из графика видно, что площадь заштр. фигуры будет равна А_1-2

Точным знач-ем будет знач-е, равное площади фигуры, огранич сверху плавн. линией. S ступенч. фигуры будет приближено к знач-ю S криволин. тр-ии, если уч-ки, на к-рые мы делим будут малыми. В пределе если сдел. уч-ки беск. малыми, можно получ. точное знач-е работы.

∆S_i 0 dS

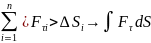
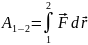
δA=F_τdr

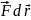δA= δA=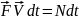

N=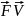

8. Кинетическая и потенциальная энергия. Механическая энергия. Консервативные силы.

Кинетич. эн-ей наз-ся скалярная величина, вид мех. эн-ии, характеризующая движ-е тел, образующих мех. сист. и числ. равная работе, к-рую необх. совершить для того, чтобы вызвать это движ-е.

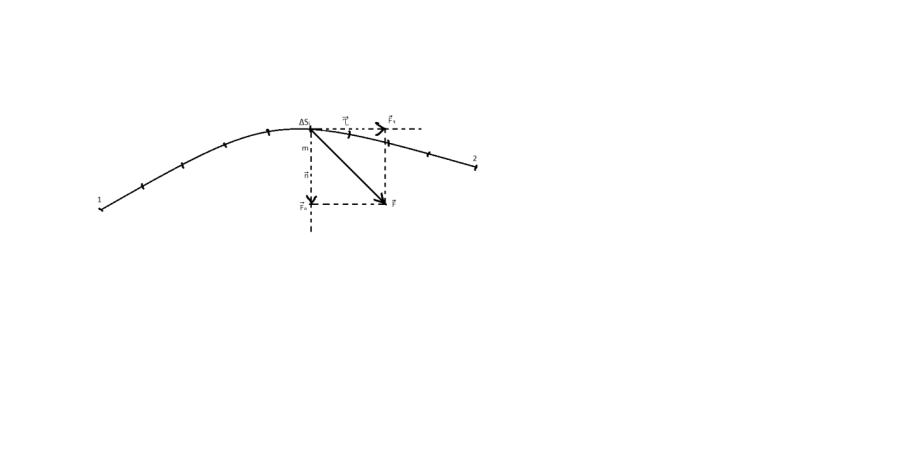
Норм. составл. приводит к искривлению траект., измен-ю движ-я (измен-е скорости). Известно, что норм. составл. силы работы не совершает. Касательная F_τ работу соверш., эта сила приводит к измен-ю модуля скорости.

=m →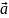

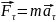
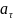=dV/dt

На участке S_i при движ-ии соверш-ся работа.

A_i=<F_τi>∆S_i→ A_i=<T_τi>∆S_i=m<a_τi>∆S_i=m∆S_i(V_i-V_i-1)/∆t_i

<F_τi>=m<a_τi>

<a_τi>=(V_i-V_i-1)/∆t_i

<V_i>=∆S_i/∆t_i

Если ∆S_i мала, то ср. скор. можно оценить как ср. арифм. скоростей в начале и в конце.

<V_i>=(V_i-V_i-1)/2

A_i=mV_i²/2-mV_i-1²/2

W_k=mV²/2

A_1-2= mV_n²/2-mV₀²/2

A_1-2= W_k2-W_k1

Потенциальная энергия обуславливается взаимодействием тел и зависит от их взаимн. полож-я.

Сила будет счит-ся консервативной, если работа этой силы опред-ся лишь начальным и конечным полож-ем точки прилож-я силы, но не зависит от вида (ф-мы) трактории движ-я точки прилож-я силы, при усл-ии, что нач. и конечн. точки всех рассматр. траекторий совп.

Для консерв. сил справедл. утв-е, что если направл-е движ-я тчк прил-я консерв. силы измен-ся на противопол, то измен-ся знак проекции консер. силы на направление движ-я, при этом работы конс. силы будет менять свой знак.

Работа консерв. силы на любой замкн. траектории перемещ-я тчк прилож. силы должна быть равна 0.

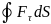– работа, соверш. силой на замкн. траектории

Если эта сила консерв., то работа для замкн. траектории должна быть равна 0.

В физике механическая энергия описывает сумму потенциальной и кинетической энергии, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Приращение полн. механич. эн-ии сист. равно суммарн. работе всех непотенц. сил, действ. на сист. Полная мех. эн-я сист, на к-рую действ. лишь консерв. силы либо действ. и не консерв. силы, но при усл-ии, что последние не совершают работы, остаётся постоянной.

Систему тел, внутри к-рой действ. лишь консерв. силы либо действ. и не консерв. силы, но при усл-ии, что неконсерв. силы работы не соверш., будем называть консервативной системой.